PID神经网络控制原理及BP神经网络PID控制仿真案例

前言

其实前面也介绍了整定PID的智能算法，如“优胜劣汰”思想的遗传算法和粒子群算法，这类智能算法的特点是：给定输入，选定目标函数进行不断寻优，最终找到一组最优参数。个人觉得这种算法的弊端在于，虽然能够得到寻得最优解，但是所谓的参数并非“动态”自适应。本篇文章介绍的神经网络自适应的特点是，实时在线进行动态寻优，并且参数是变化的。

可能这里叙述这么多，初学者觉得还是一头雾水，接下来作者将通过仿真分析，依次介绍单神经元、BP神经网络、RBF神经网络整定PID的方法，其实其他的神经网络或者控制器以及参数都可按照类似思想进行构建。

网上也有大量类似文章并附有有源程序，但是其实很多都是内容得不到相应结果，或者是纯m语言的仿真，不适合普及仿真分析，所以再思用simulink模型进行仿真分析测试神经网络整定参数的效果。作者也是刚学习完这部分内容，有高见还望读者指出，谢谢理解！

1  基于单神经元自适应PID Simulink仿真分析

1.1 原理简介

单神经元自适应PID原理框架

上图中：

①x1、x2、x3为PID的离散形式变量，这里以增量式PID为例，即x1=e；x2=e-e_1；x3=e-2e_1+e_2。

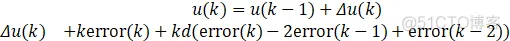
②K为神经原比例系数，K>0，值得说明一下K的选择：K越大，响应越快，单超量增大，甚至可能导致系统不稳定，当系统存在延时环节时，K必须减小以保证系统稳定性。

单神经元的具有结构简单，且有一点自适应能力的特点，也是神经网络的基本框架衍生，对于初学者学习是很友好的，所以也有典型的几种学习规则，顾名思义，就是权重学习方法进行分支，下面先简单介绍一下：

1.1.1 无监督的Hebb学习

学习规则：

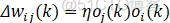
式中：wij为神经元i和神经元j的连接权值，oi和oj表示神经元i、j的激活值，η为学习速率。

无监督的Hebb学习的自适应PID算法：

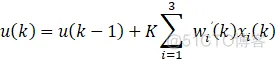
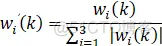
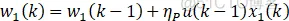
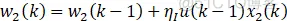
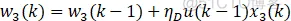
x1、x2、x3为增量式PID的变量，即：

1.1.2 有监督的Delta学习

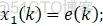
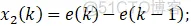
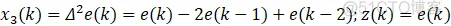
学习规则：

相比无监督的Hebb学习，其实就是将oj替换成目标输出dj与实际输出oj之差。

有监督的Delta学习自适应PID算法：

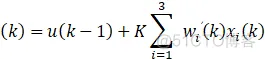
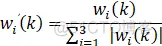
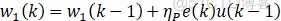
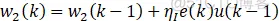
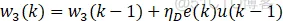
注：有监督的Hebb学习规则类似，只不过权值中不包含xi误差变量。

1.1.3 有监督的Hebb学习

学习规则：

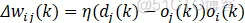
其实就是将无监督的Hebb学习规则和有监督的Delta学习规则结合构成有监督的Hebb学习规则。

有监督的Hebb学习自适应PID算法：

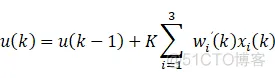
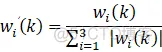
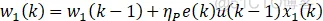
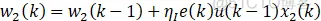
x1、x2、x3为增量式PID的变量，即：

1.1.4 改进的有监督Hebb学习

学习规则和有监督的Hebb一样，只不过将权值中的误差变量x替换成e+Δe(k)。

改进的有监督Hebb学习自适应PID算法：

权值中的PID变量xi为：

1.1.5 总结

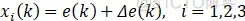
有点烟花缭乱，但其实就是权值的学习规则差异，再简明点即权值公式小差异，汇总一下 ：

1.2 simulink仿真分析

对于simulink这边个人喜欢用s函数去编写模型和控制器，这样更为简介，所以编写程序前先要进行框架构建，考虑一个问题：是否需要状态变量？

个人觉得有3种方法：

①选择wi为离散状态变量；

②不需要状态变量，设定局部或全局状态变量，相当于内部循环；

③不需要状态变量，利用延时模块得到前一时刻的信息进行编写。

结果差异肯定会有一些，但其实过程大同小异！下面我都将进行编写仿真分析，但是由于编写方式不一样，所以参数调节也不一样，故效果仅供参考。

仿真模型：

1.2.1 将权值作为状态变量仿真分析

1.2.2 利用局部变量定义权值仿真分析

1.2.3 利用延时模块仿真分析

1.2.4 仿真小结

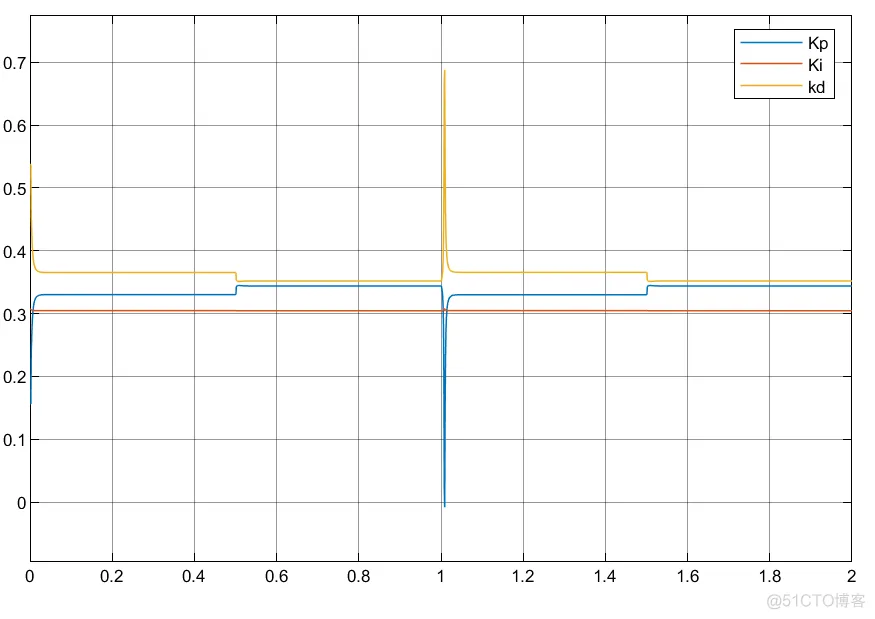
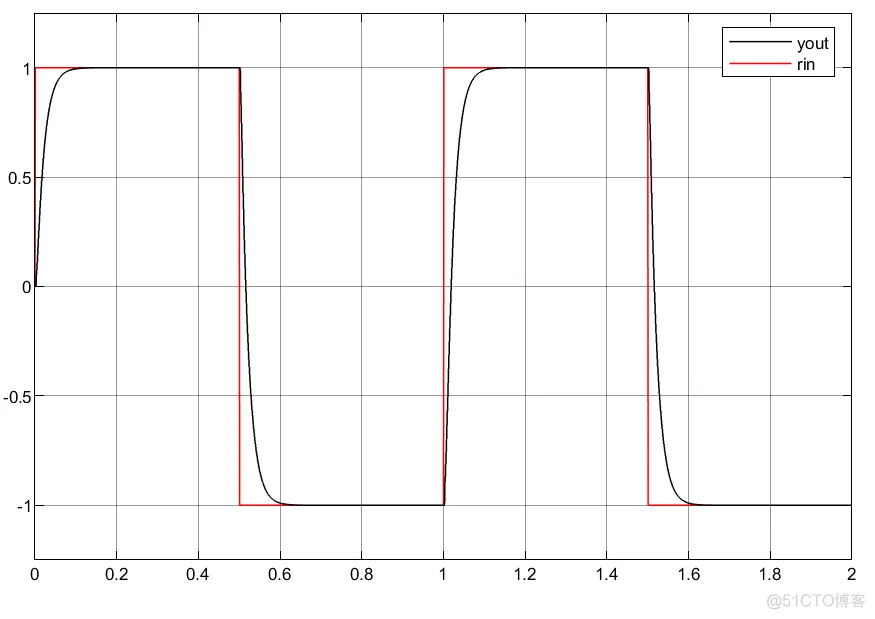
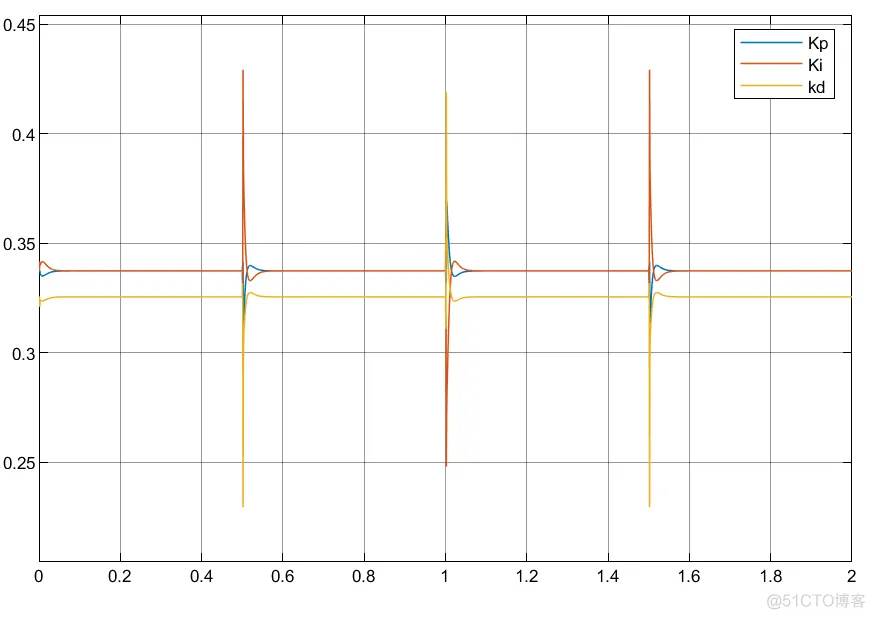
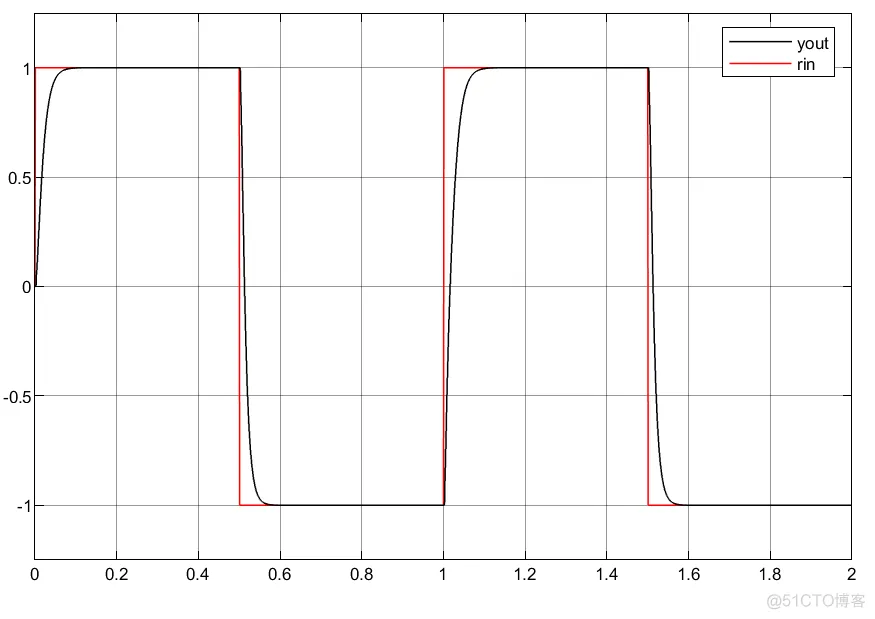
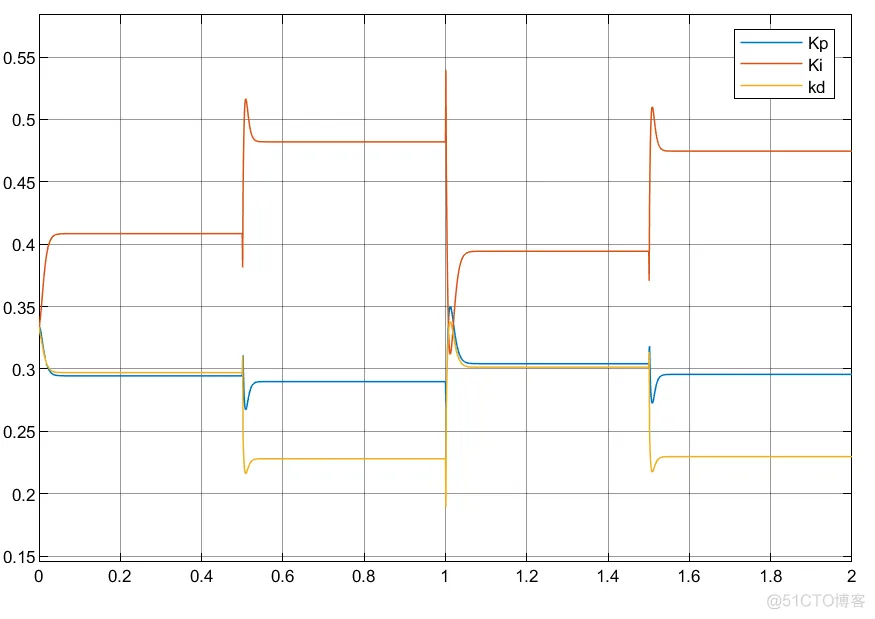
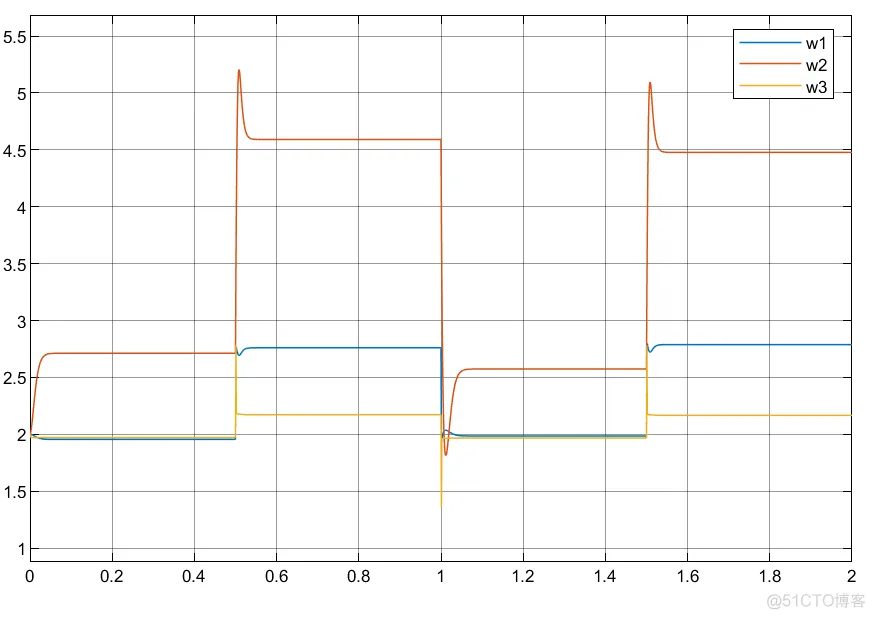
①可以看到利用延时模块的搭建控制器参数自适应更为缓和；

②实际中利用状态变量搭建控制器系统更为稳定以及简洁。

2  基于BP神经网络自适应PID Simulink仿真分析

2.1 原理简介

BP神经网络全称是前向传播神经网络，又名反向传播神经网络，一般由3层网络组成：输入层、隐含层(隐层)、输出层。

BP网络结构

下面分别对基于BP网络与PID结合算法：

①输入层：

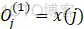
其中，j=1,2....M表示输入变量的个数，数量取决于控制系统复杂度。

②隐层：

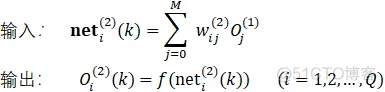
式中，上标(1)、(2)代表输入层、隐层；f为激活函数，可选为sigmoid函数中的tanh(x)

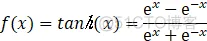
③输出层：

既然是输出，那就需要定义何时输出最优值，所以定义性能指标E=e^2.

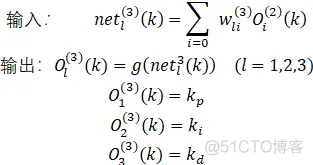
式中，由于PID参数一般为非负数，所以激活函数g选取为非负的sigmoid函数：

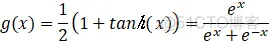
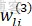
为输出层惯性项，用于快速收敛得到性能函数极小值:

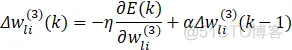
式中，η为学习速率，α为惯性系数。

由于输入就是选取变量，所以没什么好说的，最终得到隐层和输出层学习算法分别为：

隐层权值学习算法：

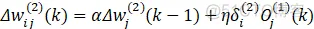
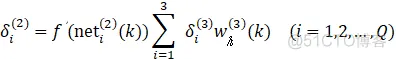
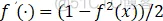
式中，Q为输出层数，这里即优化PID参数，选为3。

注：可以看到隐层惯性项中存在δ3，所以算法编写中要先编写输出层。

输出层权值学习算法：

2.2 仿真分析

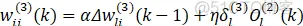
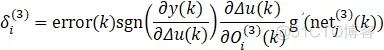
同样可以用以上3中方法进行离散控制器搭建，但是由于权重维度原因，不建议采用状态变量搭建，所以本文用局部变量和延时模块两种方法进行搭建控制器，并且为了对比结果，还是采用同1中模型和跟踪函数，方便进行比对。

仿真模型：

2.2.1 利用局部变量定义权值仿真分析

2.2.2 利用延时模块仿真分析

2.1.3 仿真小结

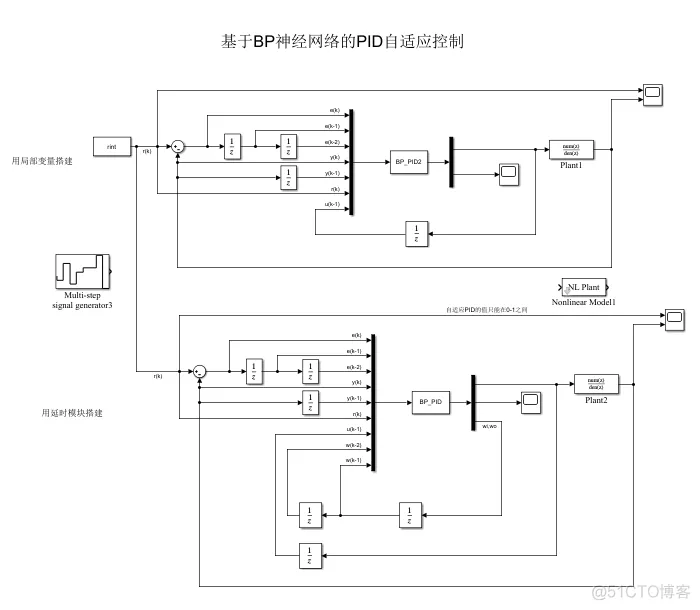
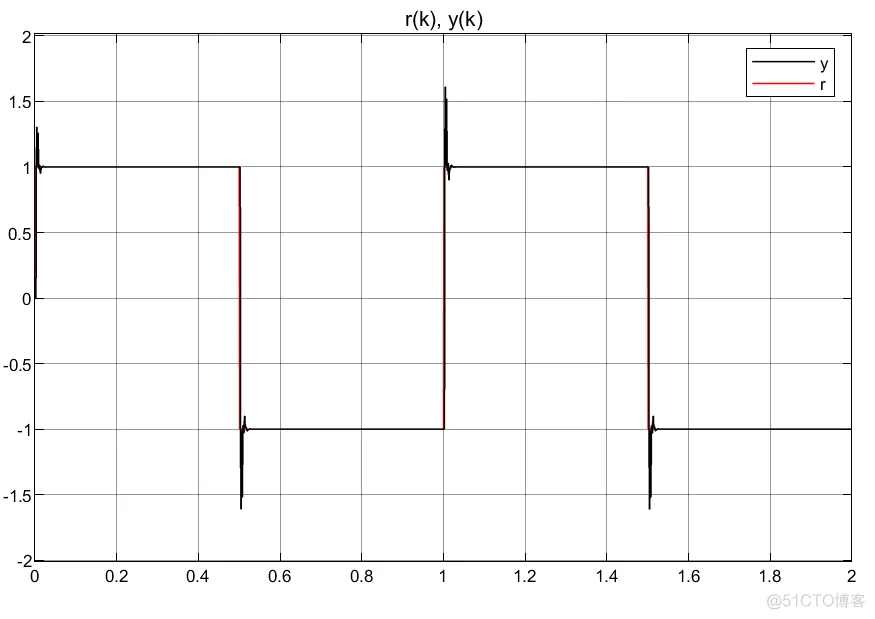
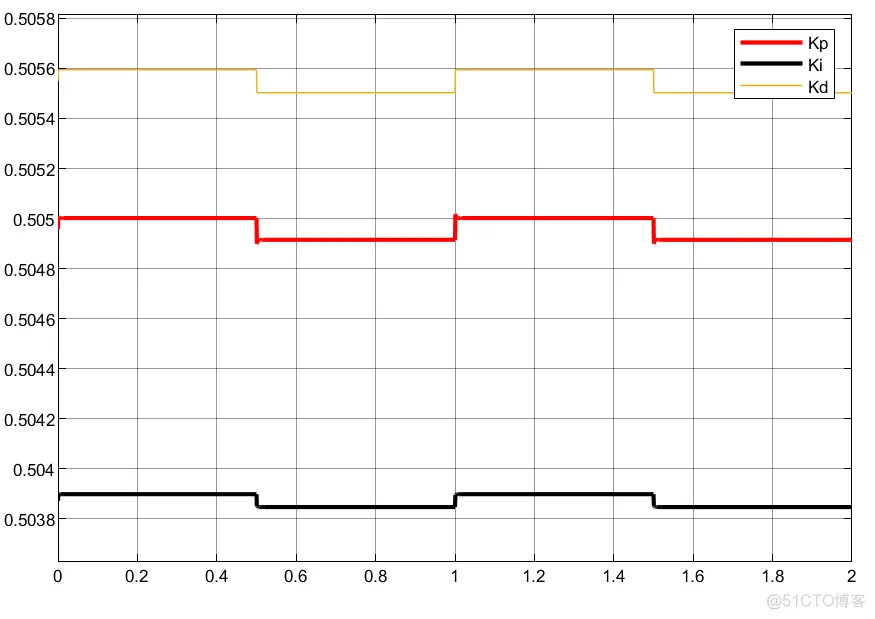
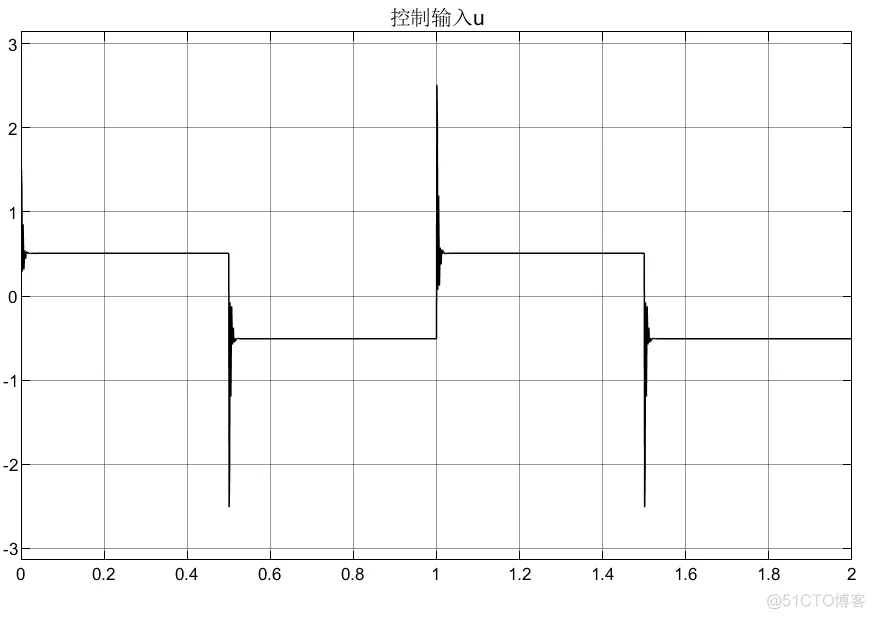
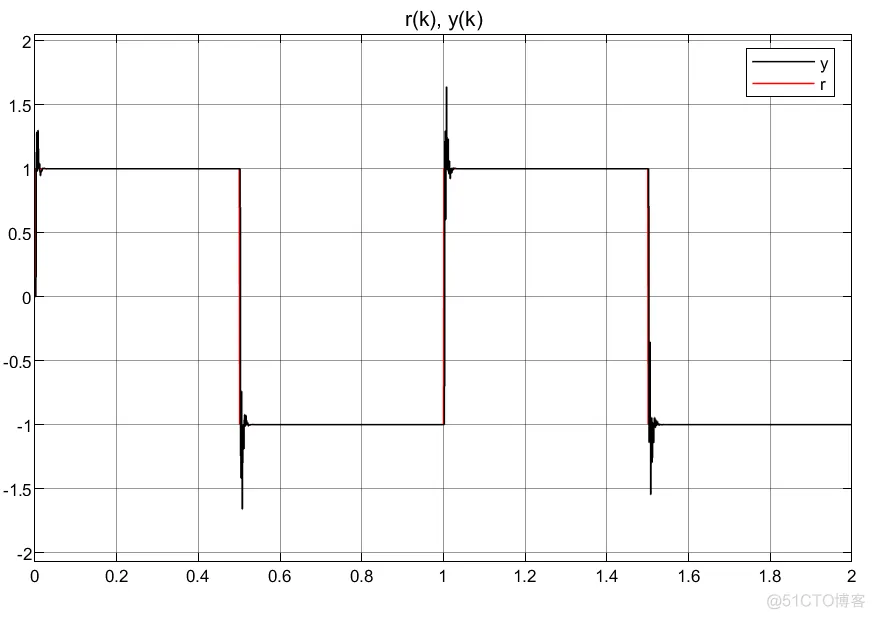
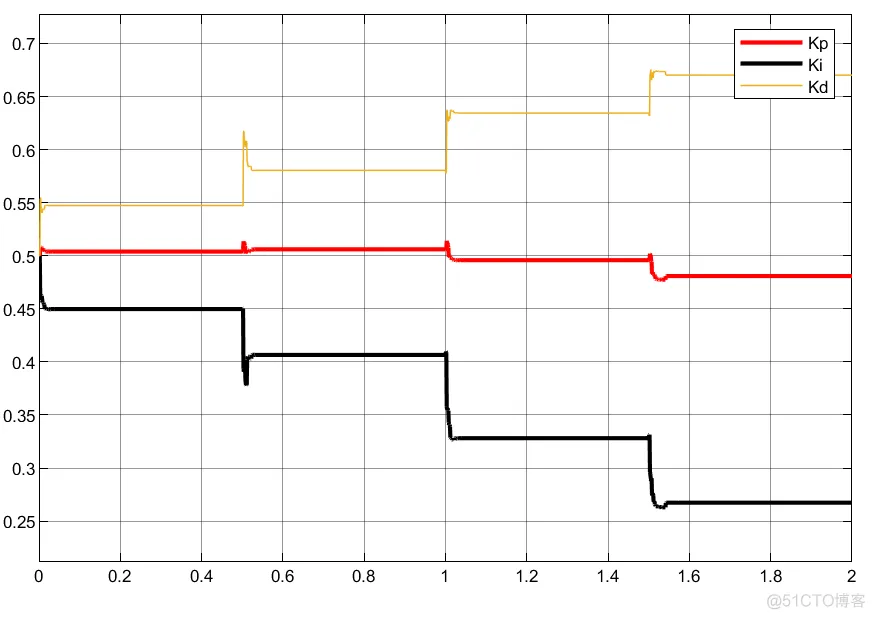
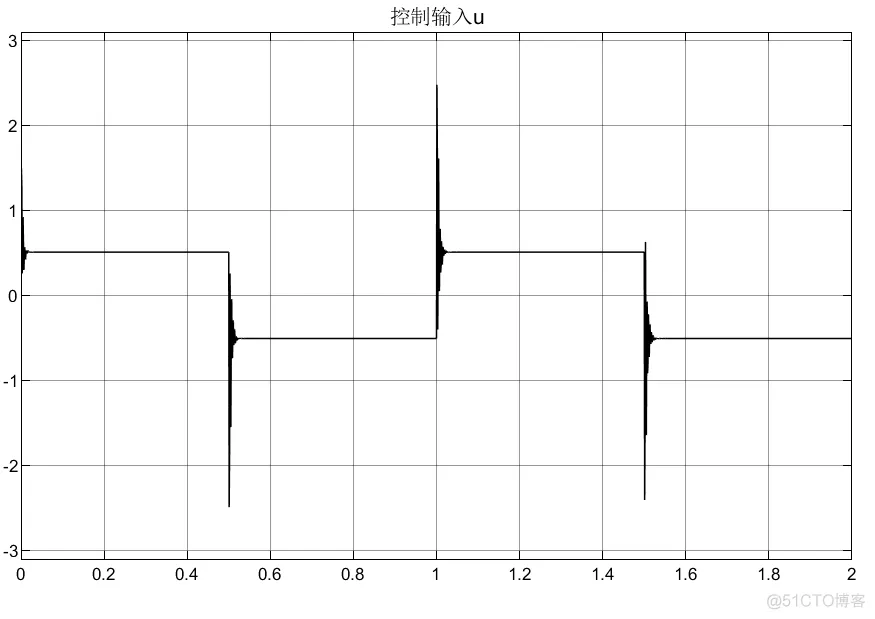
①不知道什么原因，调了几分钟，总是产生超调，但是换一个模型时又不会；

②反而比单层神经元结果更差，但是换个模型还是不错的；

③可以看到，控制器编写的方法不同，虽然控制器优化的参数会有差异，但是得到的控制输入大小和趋势相同。

3  基于RBF神经网络自适应PID Simulink仿真分析

3.1 原理简介

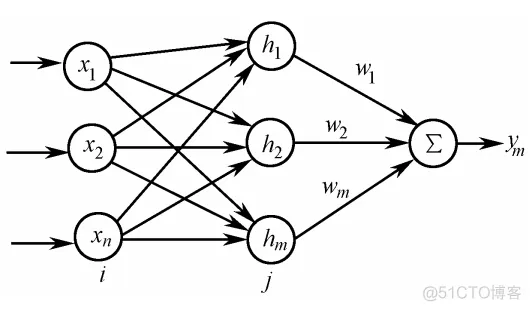
RBF网络结构

RBF神经网络全称径向基函数神经网络，它的逼近能力很强，但实际上训练能力不如BP神经网络，也是很多场合用BP网络做训练的原因所在。

RBF网络也是一种3层网络，输入映射是非线性的，常用高斯基函数作为非线性映射函数。

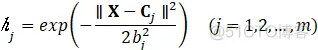
式中，X=[x1,x2,...xn]为网络输入向量， Cj=[c1,c2,...cm]为网络中心节点向量。

而隐层到输出层映射是线性的，这也从原理上大致说明其逼近能力强的特点，且避免局部极小值问题。

做如下向量定义：

H=[h1,h2,...,hm]'为RBF网络径向基向量；

B=[b1,b2,...,bm]'为RBF网络的基宽向量；

W=[w1,w2,....,wm]'为RBF网络的权向量。

所以RBF网络的输出为：y=W'*H=w1*h1+w2*h2+....wm*hm

权向量W、基宽向量B和中心节点向量C的的学习算法采用梯度下降法：

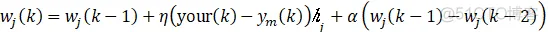
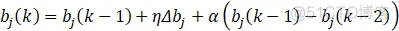
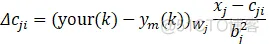
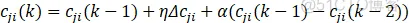
式中，η为学习速率；α为动量因子，可以理解为补偿作用。

雅可比矩阵：

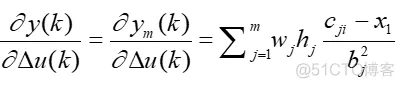
式中，x1=Δu(k)；雅可比矩阵决定了输出相对控制输入的灵敏度，求取雅可比矩阵的过程即融合了RBF网络输出的线性映射，所以可以理解为网络的辨识输出。

本文将RBF网络应用于整定PID控制参数上，所以相应的PID参数学习算法为：

3.2 仿真分析

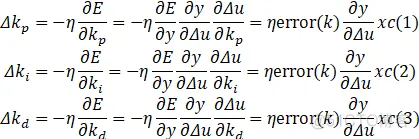
同理，仍选用与单神经元、BP神经网络相同的目标轨迹和模型，仍采用延时模块和局部/全局变量两种方式编写控制器，所建立的simulink模型展示如下：

3.2.1 采用局部/全局变量方法

3.2.2 采用延时模块方法

3.2.3 仿真小结

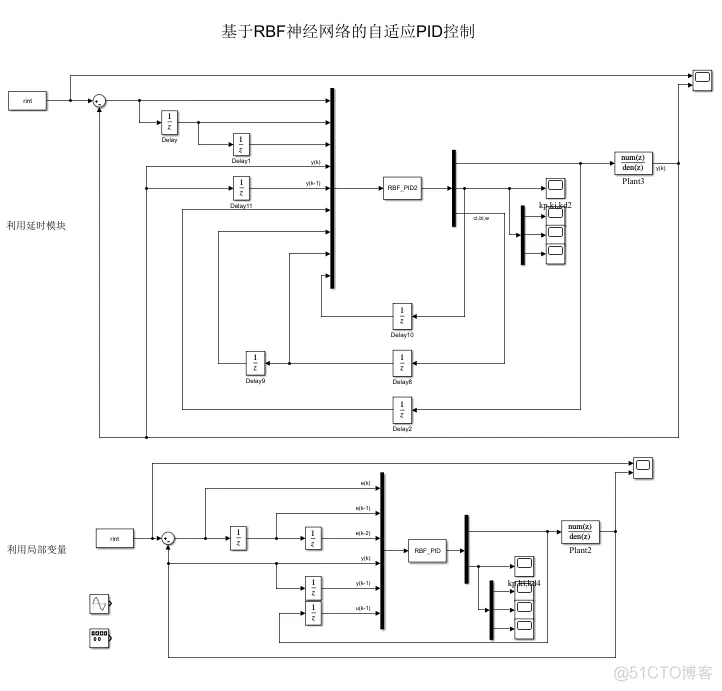
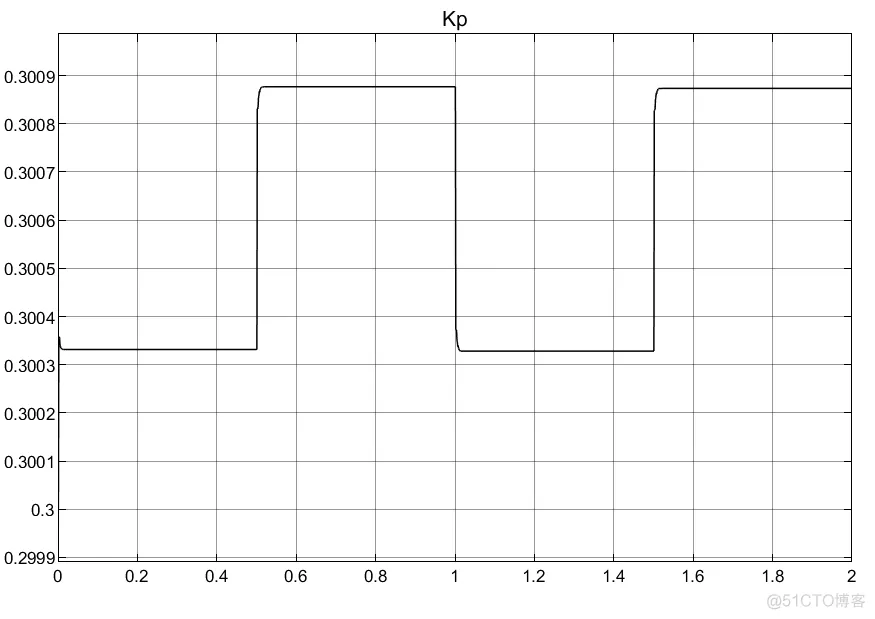
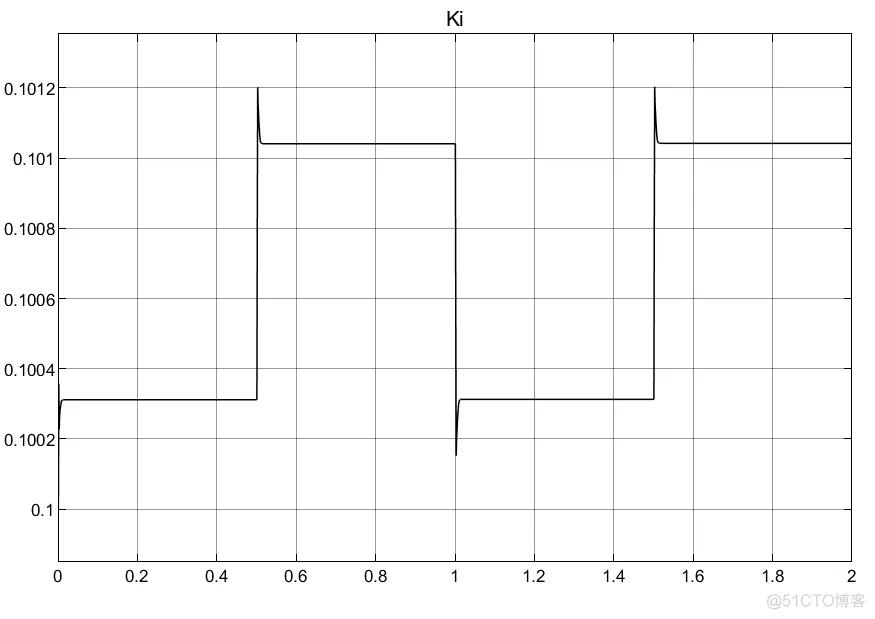
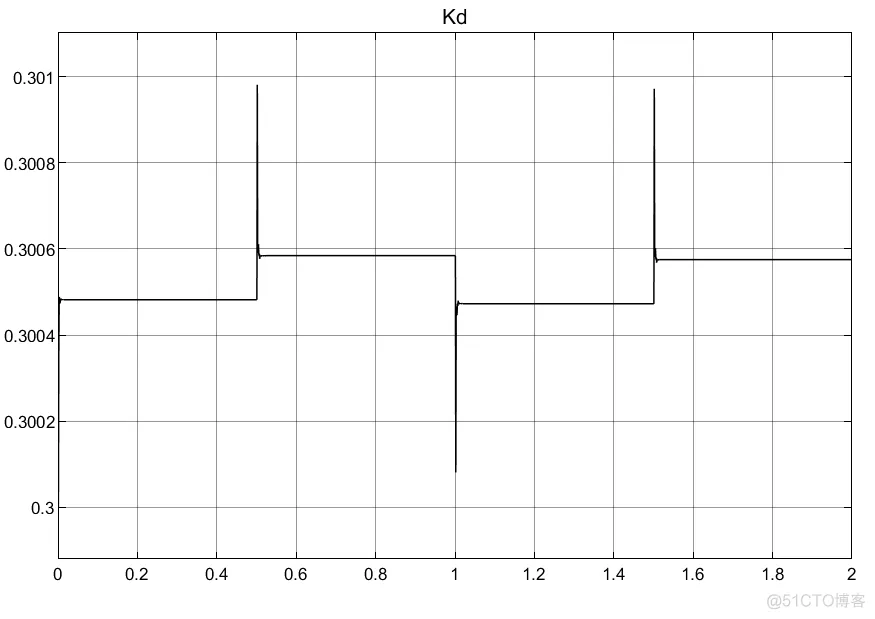
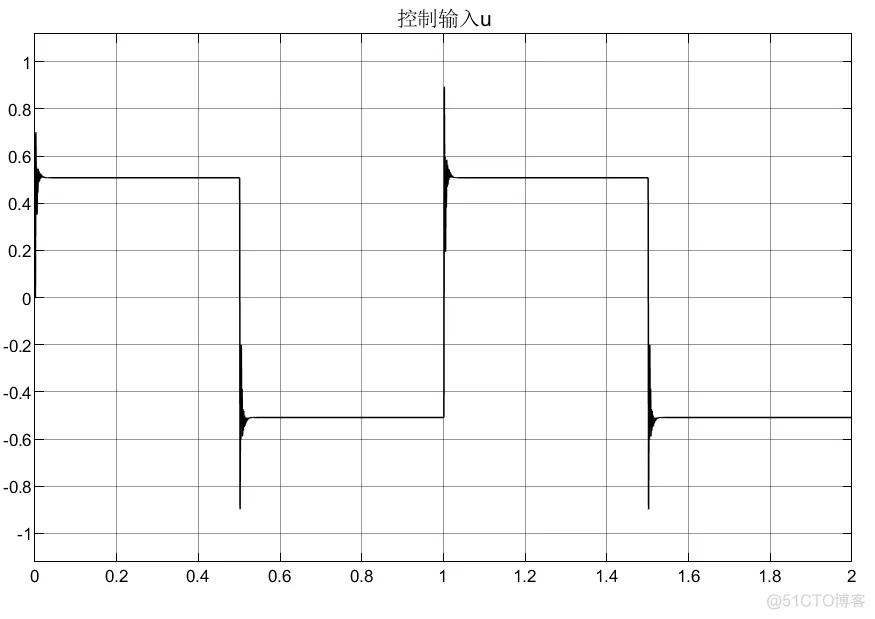
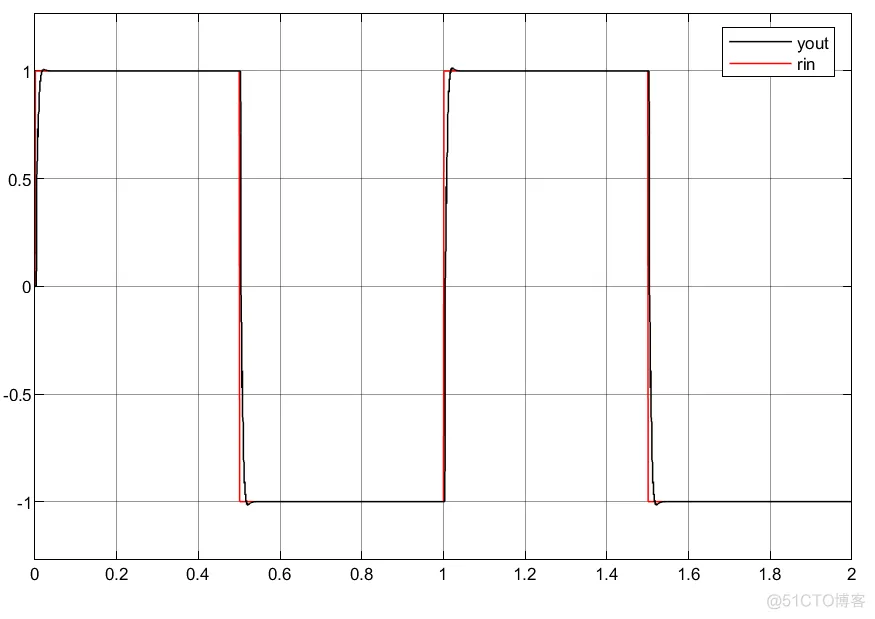
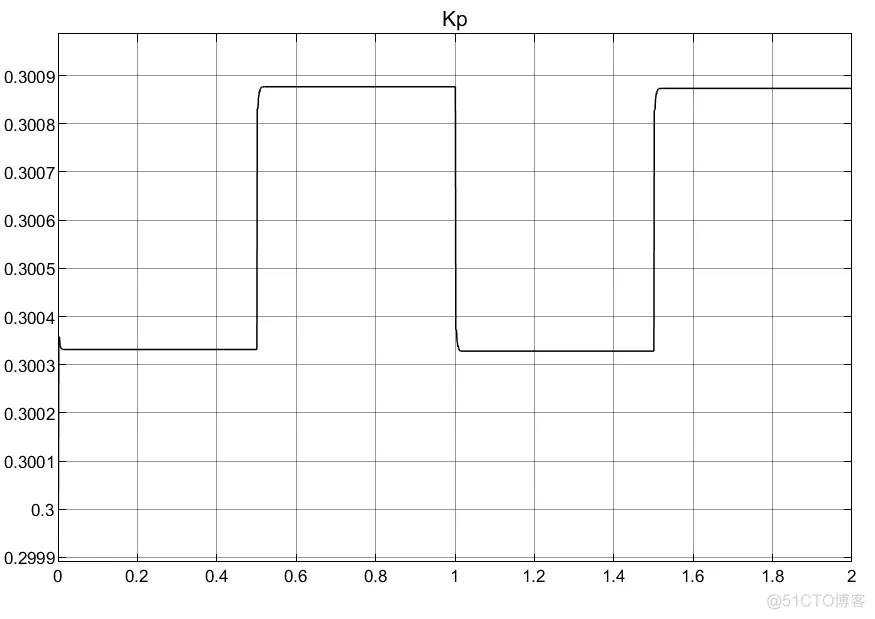
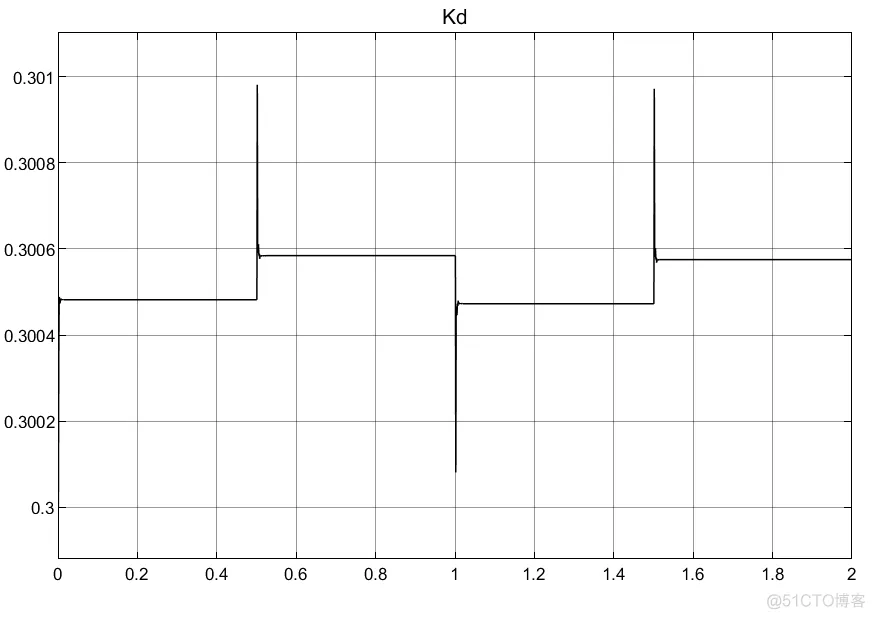
①RBF的网络对于PID参数的初值选取以及权重选取都很重要；

②两种建模方法的结果有较大差异。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删