PID控制下的四旋翼飞行器Matlab仿真实现

1 概述

近几年，随着科技发展，各种传感器技术和通信技术不断突破，无人机技术也发展迅速，在军事侦察、交通巡逻、景色航拍、高空电缆巡检等诸多应用领域已经发挥了重要的作用。四旋翼无人机以其具有的操作灵活、地形上限制小、携带时方便以及成本低廉等特点，更加紧密贴近了我们的日常生活，因此，对无人机进行研究具有很大的学术价值和意义。

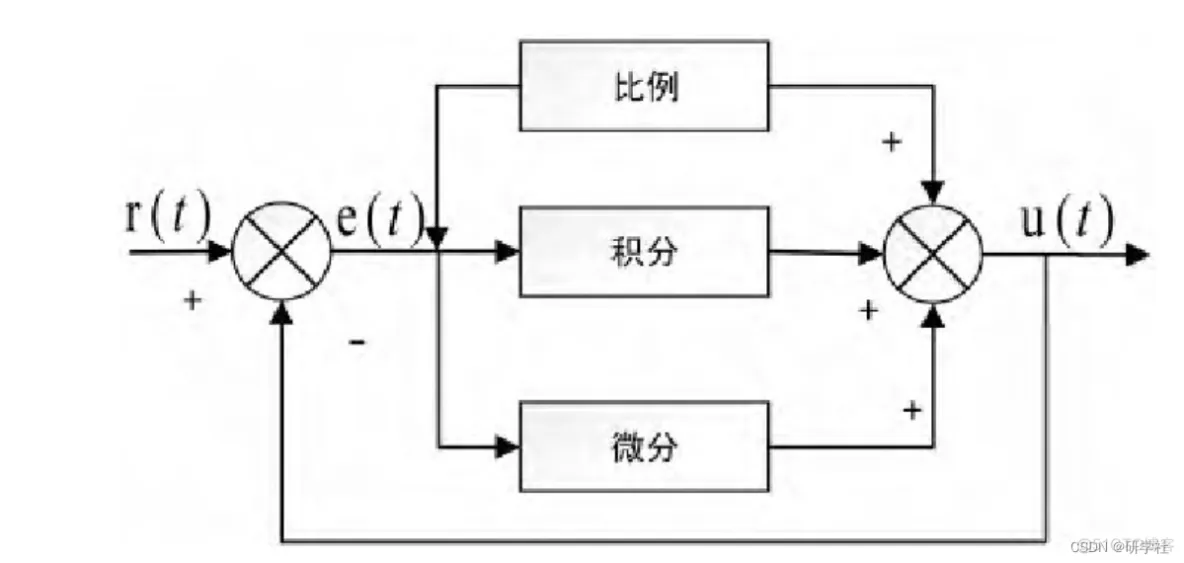
传统的PID由比例、积分、微分三部分组成，通过调节Kp、Ki、Kd的数值可以实现不同的控制效果如图所示。PID控制算法的核心是用偏差来消除偏差，该算法可以对控制系统进行有效的估计：

2 运行结果

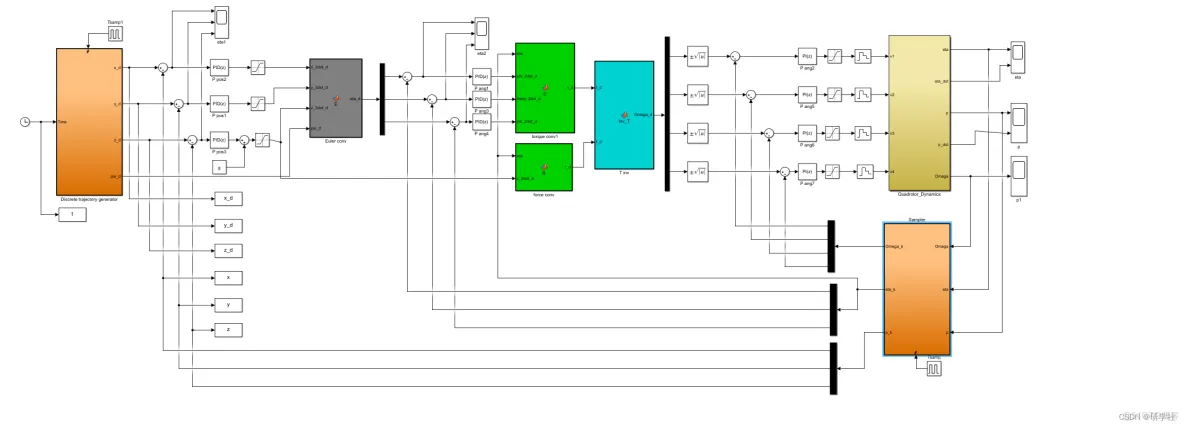
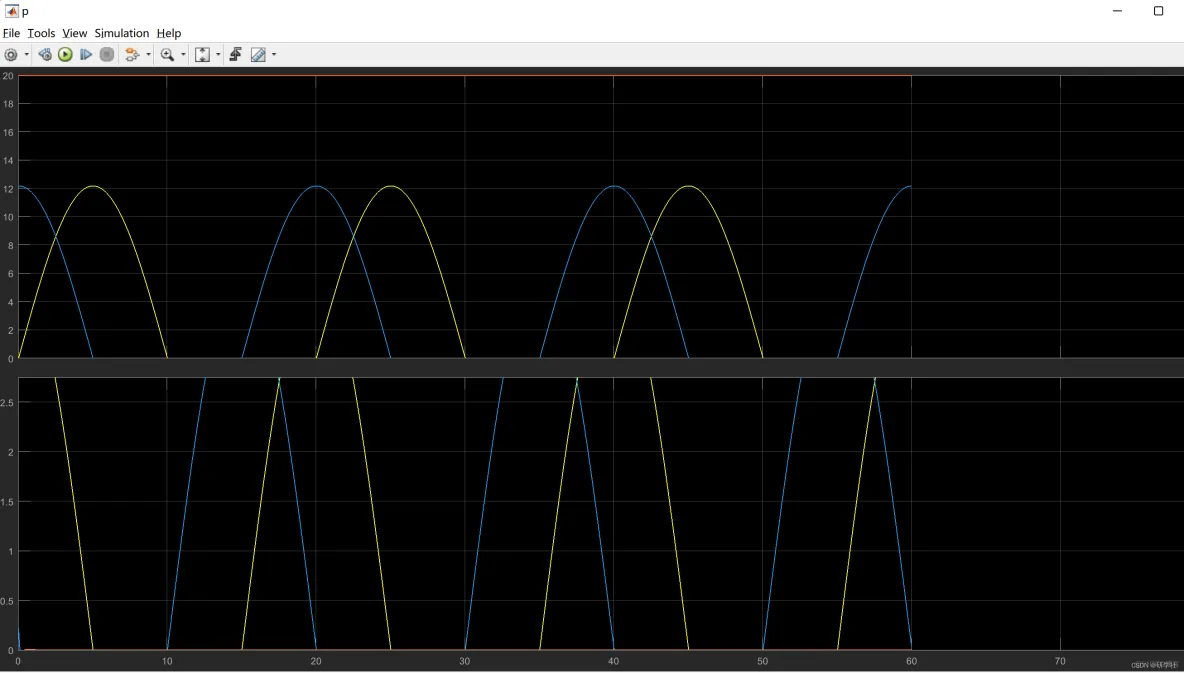
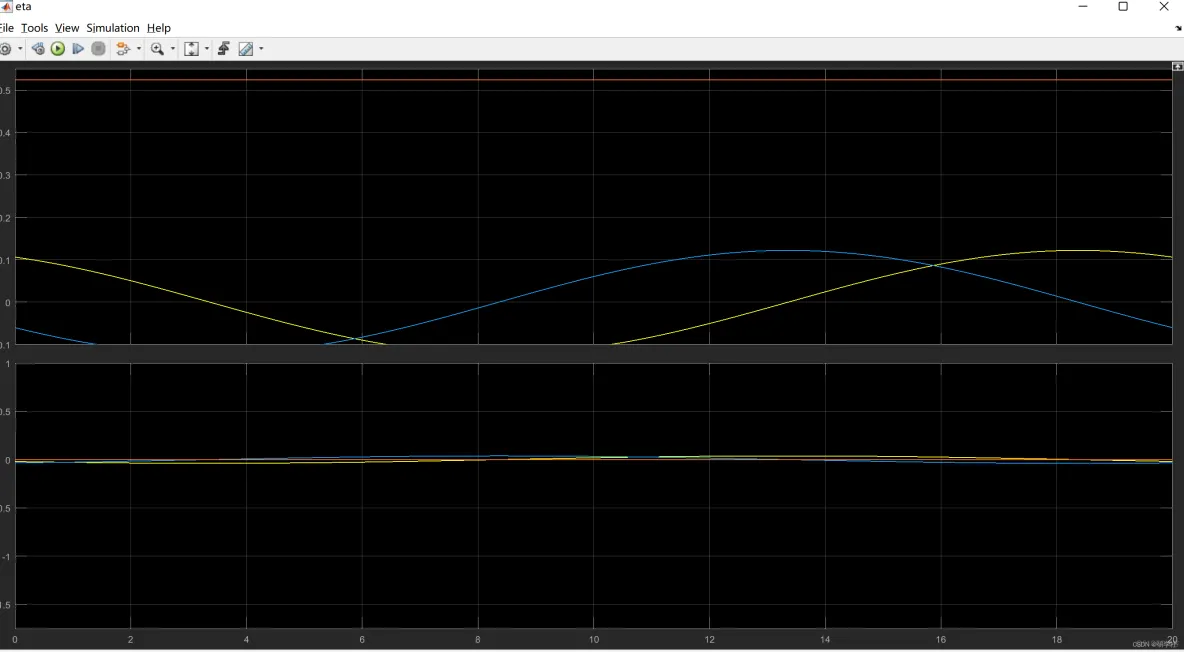
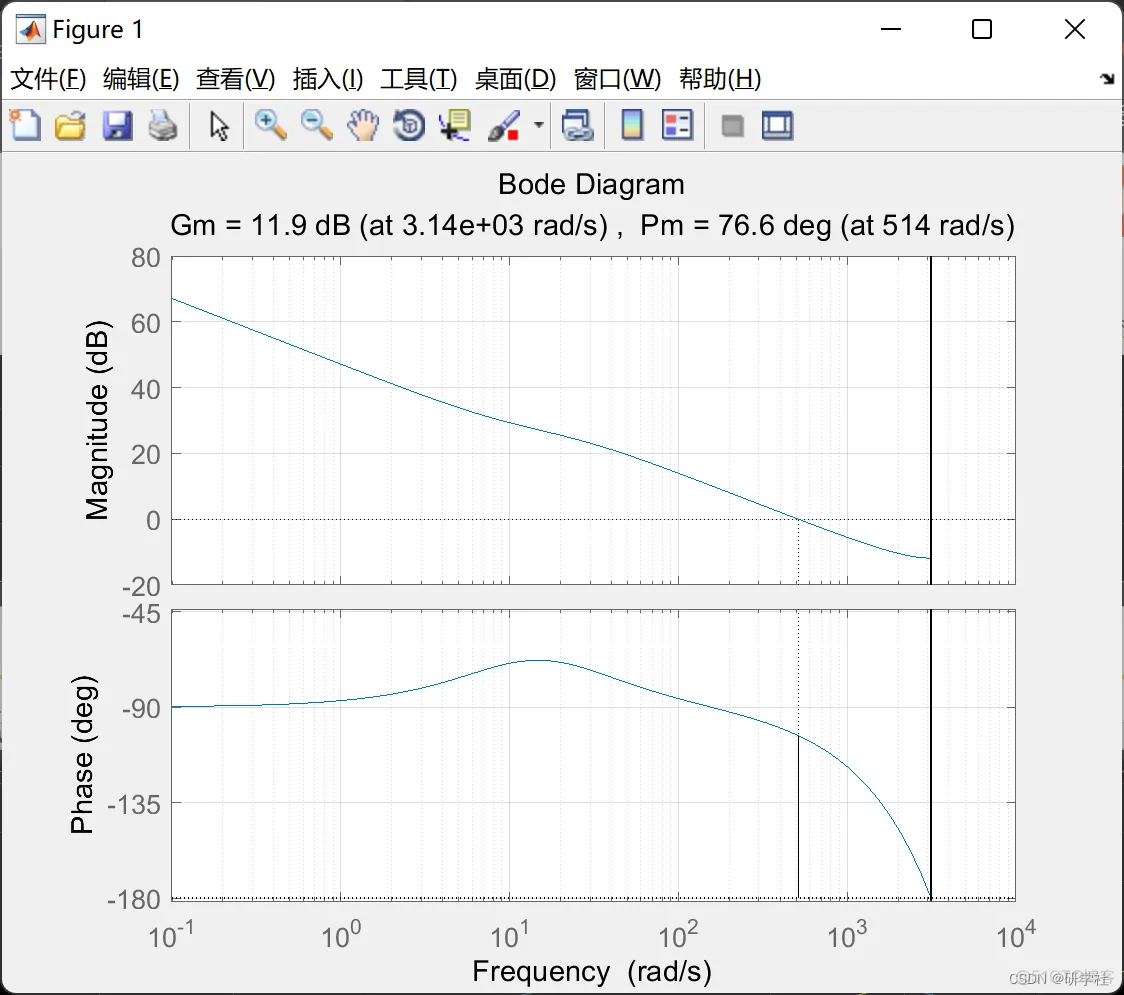
部分代码：

I = [Ixx 0 0;0 Iyy 0;0 0 Izz];
Jtp = 104e-6;
Ke = 6.3e-3;
Km = 6.3e-3;
L = 15e-6;
b = 54.2e-6;
l = 0.24;
g = 9.81;
n = 0.9;
N = 5.6;
h = 1e-3;
R = 0.6;
d = 1.1e-6; % drag factor
% Motor Controller Design

Kp_position = 5;
Ki_position = 0;
Kd_position = 10;

Kp_angle = 5*2;
Ki_angle = 0;
Kd_angle = 10*2;

Kp_motor = 1;
Ki_motor = 10;
Kd_motor = 0;

%w'=Apw+Bpv+Cp
Ap = -22.5;
Bp = 509;
Cp = 489;
a1 = Ap;
b1 = Bp;
c1 = 1;
d1 = 0;
sys_c_m = ss(a1,b1,c1,d1);
Gc_m = tf(sys_c_m);
sys_d_m = c2d(sys_c_m,h,'zoh');
Gd_m = tf(sys_d_m);

Cc_m = tf([Kp_motor Ki_motor],[1 0]);
sys_c_mctrl = ss(Cc_m);
sys_d_mctrl = c2d(sys_c_mctrl,h,'tustin');
Cd_m = tf(sys_d_mctrl);

LGd_m = Gd_m*Cd_m;
Td_m = feedback(LGd_m,1);

figure(1)
margin(LGd_m)
hold on
grid on
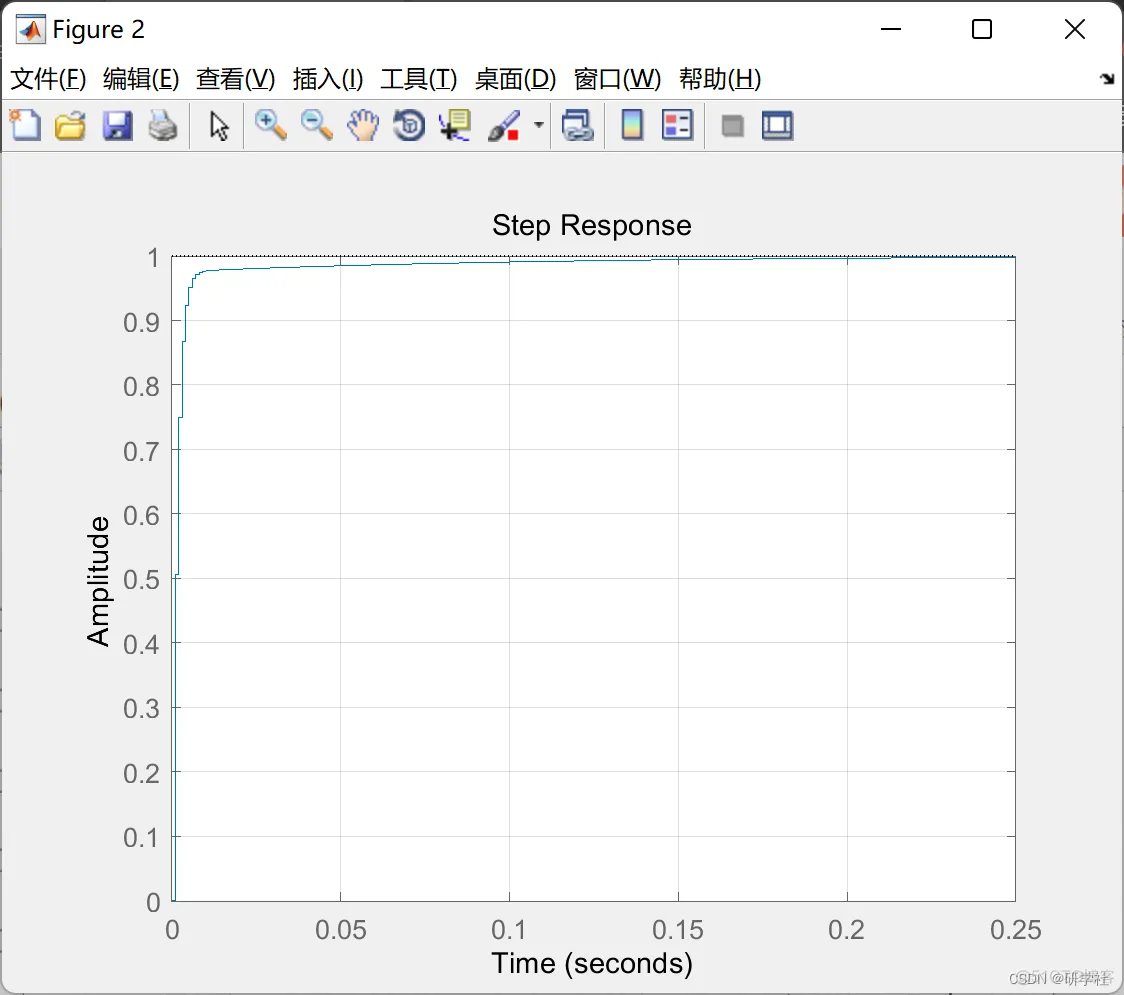
figure(2)
step(Td_m)
hold on
grid on

num = [1];
den = [1 0 0];
Gc_p = tf(num,den);
sys_c_p = ss(Gc_p);
sys_d_p = c2d(sys_c_p,h,'zoh');
Gd_p = tf(sys_d_p);

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删

武汉格发信息技术有限公司，格发许可优化管理系统可以帮你评估贵公司软件许可的真实需求，再低成本合规性管理软件许可,帮助贵司提高软件投资回报率，为软件采购、使用提供科学决策依据。支持的软件有: CAD,CAE,PDM,PLM,Catia,Ugnx, AutoCAD, Pro/E, Solidworks ,Hyperworks, Protel,CAXA,OpenWorks LandMark,MATLAB,Enovia,Winchill,TeamCenter,MathCAD,Ansys, Abaqus,ls-dyna, Fluent, MSC,Bentley,License,UG,ug,catia,Dassault Systèmes,AutoDesk,Altair,autocad,PTC,SolidWorks,Ansys,Siemens PLM Software,Paradigm,Mathworks,Borland,AVEVA,ESRI,hP,Solibri,Progman,Leica,Cadence,IBM,SIMULIA,Citrix,Sybase,Schlumberger,MSC Products...