1.算法仿真效果
matlab2022a仿真结果如下:
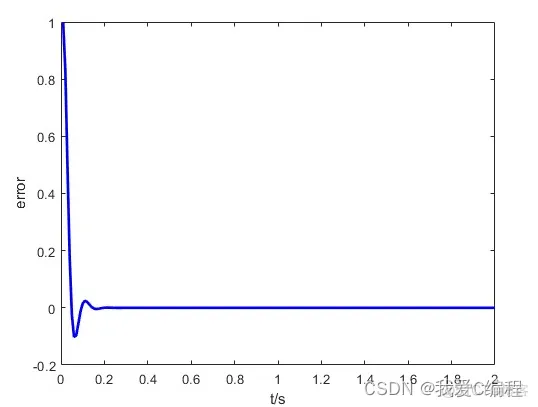
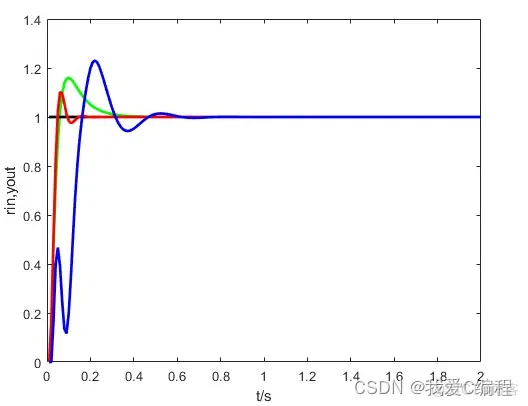
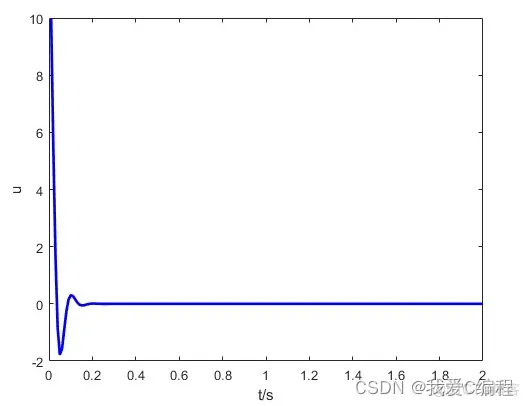
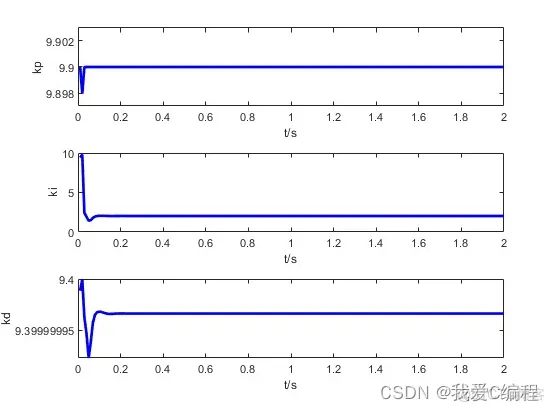
2.算法涉及理论知识概要
PID控制器(比例-积分-微分控制器),由比例单元 P、积分单元 I 和微分单元 D 组成。通过Kp, Ki和Kd三个参数的设定。PID控制器主要适用于基本线性和动态特性不随时间变化的系统。
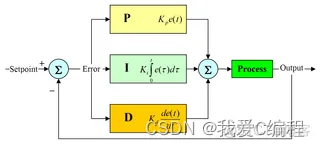
PID 控制器的方块图PID 控制器是一个在工业控制应用中常见的反馈回路部件。这个控制器把收集到的数据和一个参考值进行比较,然后把这个差别用于计算新的输入值,这个新的输入值的目的是可以让系统的数据达到或者保持在参考值。和其他简单的控制运算不同,PID控制器可以根据历史数据和差别的出现率来调整输入值,这样可以使系统更加准确,更加稳定。可以通过数学的方法证明,在其他控制方法导致系统有稳定误差或过程反复的情况下,一个PID反馈回路却可以保持系统的稳定。
具有比例-积分-微分控制规律的控制器,称PID控制器。这种组合具有三种基本规律各自的特点,其运动方程为:
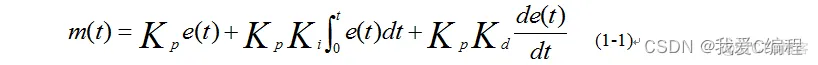
由此可见,当利用PID控制器进行串联校正时,除可使系统的型别提高一级外,还将提供两个负实零点。与PI控制器相比,PID控制器除了同样具有提高系统的稳态性能的优点外,还多提供一个负实零点,从而在提高系统动态性能方面,具有更大的优越性。因此,在工业过程控制系统中,广泛使用PID控制器。PID控制器各部分参数的选择,在系统现场调试中最后确定。通常,应使积分部分发生在系统频率特性的低频段,以提高系统的稳态性能;而使微分部分发生在系统频率特性的中频段,以改善系统的动态性能。
但是传统比例-积分-微分(Proportion Integral Derivative,PID)控制器存在参数整定困难,不能在线实时调整以及面对复杂非线性系统时应用效果不佳等问题,提出一种基于粒子群算法(Particle Swarm Optimization,PSO)优化的反向传播(Back Propagation,BP)神经网络PID控制方法。将BP神经网络与PID控制器相结合,利用BP神经网络的自适应学习能力在线实时调整PID控制参数,提升系统稳定性,针对BP-PID自学习过程中容易陷入局部极小值问题,利用改进的PSO算法对其进行优化,确保BP-PID系统收敛于全局最优解。基于仿真数据开展实验,结果表明,所提方法能够有效提升系统的控制精度和控制稳定度。
PSO算法是一种随机的、并行的优化算法。它的优点是:不要求被优化函数具有可微、可导、连续等性质,收敛速度较快,算法简单,容易编程实现。然而,PSO算法的缺点在于:(1)对于有多个局部极值点的函数,容易陷入到局部极值点中,得不到正确的结果。造成这种现象的原因有两种,其一是由于待优化函数的性质;其二是由于微粒群算法中微粒的多样性迅速消失,造成早熟收敛。这两个因素通常密不可分地纠缠在一起。(2)由于缺乏精密搜索方法的配合,PSO算法往往不能得到精确的结果。造成这种问题的原因是PSO算法并没有很充分地利用计算过程中获得的信息,在每一步迭代中,仅仅利用了群体最优和个体最优的信息。(3)PSO算法虽然提供了全局搜索的可能,但是并不能保证收敛到全局最优点上。(4)PSO算法是一种启发式的仿生优化算法,当前还没有严格的理论基础,仅仅是通过对某种群体搜索现象的简化模拟而设计的,但并没有从原理上说明这种算法为什么有效,以及它适用的范围。因此,PSO算法一般适用于一类高维的、存在多个局部极值点而并不需要得到很高精度解的优化问题。
当前针对PSO算法开展的研究工作种类繁多,经归纳整理分为如下八个大类:(1)对PSO算法进行理论分析,试图理解其工作机理;(2)改变PSO算法的结构,试图获得性能更好的算法;(3)研究各种参数配置对PSO算法的影响;(4)研究各种拓扑结构对PSO算法的影响;(5)研究离散版本的PSO算法;(6)研究PSO算法的并行算法;(7)利用PSO算法对多种情况下的优化问题进行求解;(8)将PSO算法应用到各个不同的工程领域。以下从这八大类别着手,对PSO算法的研究现状作一梳理。由于文献太多,无法面面俱到,仅捡有代表性的加以综述。
PSO初始化为一群随机粒子(随机解)。然后通过迭代找到最优解。在每一次迭代中,粒子通过跟踪两个“极值(pbest和gbest)”来更新自己。在找到这两个最优值后,粒子通过下面的公式来更新自己的速度和位置。

3.MATLAB核心程序
net2=xi*(wi');
for j=1:1:H
Oh(j)=( exp( net2(j)-exp(-net2(j)) ) )/(exp( net2(j)+exp(-net2(j)) ));
end
net3=wo*Oh;
for l=1:1:Out
K(l)=exp(net3(l))/(exp(net3(l))+exp(-net3(l)));
end
kp(k)=M(1)*K(1); ki(k)=M(2)*K(2); kd(k)=M(3)*K(3);
Kpid=[kp(k),ki(k),kd(k)];
du(k)=Kpid*epid;
u(k)=u_1+du(k);
if u(k)>10
u(k)=10;
end
if u(k)<-10
u(k)=-10;
end
%%%后向传播------------------------------------------------
dyu(k)=sign((yout(k)-y_1)/(du(k)-du_1+0.0001));
for j=1:1:Out
dK(j)=1/(exp(net3(j))+exp(-net3(j)));
%dK(j)=M;
end
for l=1:1:Out
delta3(l)=error(k)*dyu(k)*epid(l)*dK(l);
end
for l=1:1:Out
for i=1:1:H
d_wo=xite*delta3(l)*Oh(i)+alfa*(wo_1-wo_2);
end
end
wo=wo_1+d_wo+alfa*(wo_1-wo_2);
for i=1:1:H
dO(i)=4/(exp(net2(i))+exp(-net2(i)))^2;
end
segma=delta3*wo;
for i=1:1:H
delta2(i)=dO(i)*segma(i);
end
d_wi=xite*delta2'*xi;
wi=wi_1+d_wi+alfa*(wi_1-wi_2);
wo_2=wo_1; wo_1=wo;
wi_2=wi_1; wi_1=wi;
du_1=du(k);
u_7=u_6;u_6=u_5;u_5=u_4; u_4=u_3;u_3=u_2;u_2=u_1;u_1=u(k);
y_2=y_1; y_1=yout(k);
error_2=error_1; error_1=error(k);
end
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删