卷积编码与维特比译码误码率仿真：基于Matlab的实现

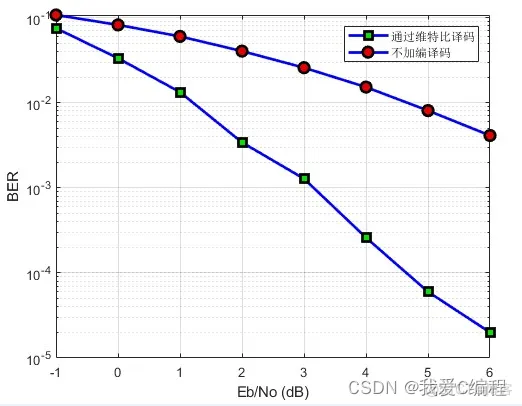
1.算法仿真效果

matlab2022a仿真结果如下：

2.算法涉及理论知识概要

随着现代通信的发展，人们对信息传输的可靠性和有效性的要求也越来越高。维特比译码算法被广泛的应用，因此如何提高维特比译码器的性能，降低译码器的功耗和面积是个重要的问题。卷积码是Elias等人在1955年提出的，是一种非常有前途的编码方法，尤其是在其最大似然译码算法-Viterbi译码算法提出之后，卷积码在通信系统中得到了极为广泛的应用。其中约束长度K=7，码率为1/2和1/3的卷积码己经成为商业卫星通信系统中的标准编码方法。在“航海家“以及“先驱者”等太空探测器上也都采用了卷积码作为其差错控制编码方法。在移动通信领域，GMS采用约束长度K=5，码率为1/2的卷积码；在IS-95中，上行链路中采用的是约束长度K=9，码率为1/3的卷积码，在下行链路中采用的是约束长度K=9，码率为1/2的卷积码。特别在第三代移动通信标准中也是以卷积码以及与卷积码相关的编码方法作为差错控制编码方案的。

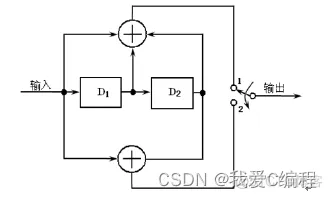
2.1卷积码编码器

登录后复制

一个输入移位寄存器（分为N段，每段k位）；n个模2加法器；一个输出数据选择器（n选一）。某一时刻，输入到编码器的k个信息元组成一个信息组，相应的输出序列是由n个码元组成的码段。这里，称N为编码约束度，说明编码过程中互相约束的码段个数。令N=m+1，则m称为编码存储，它表示输入信息组在编码器中需存储的单位时间（有时为了简化，编码器中只用m段的输入移位寄存器）。称Nn为编码约束长度，说明编码过程中互相约束的码元个数，如m=2，n=2，则Nn=6。所以m或N以及Nn都是表示卷积码编码器复杂性的重要参数。

编码电路：

2.2维特比译码

卷积编码的过程就是编码器状态沿着时间轴一级一级跳转的过程。维特比译码算法则是在网格图上搜索最可能的状态跳转路径的过程。维特比译码算法先读取t时刻的所有状态的幸存路径度量，再根据t+1时刻的输入，算出跳转路径的度量:根据这两类度量算出t+1时刻到状态S的所有路径的度量，比较选出一个具有较小路径度量的路径作为t+l时刻状态S的幸存路径。这样对每个状态都得到一个幸存路径，根据这些幸存路径和最终编码器所处的状态就可以得到编码器的状态转移路径即译码结果。维特比译码结果的可信度取决于幸存路径的深度和它的路径度量值。幸存路径越深、路径度量值越高，那么译出信息的可信度就越高。在译码过程中有些路径被抛弃了，有些路径被保留了下来。被以为是幸存路径的，也可能会在后面的搜索过程中被抛弃掉。这样随着搜索的深度不断加深，最终正确的路径将会被保留下来，所有的幸存路径都将收敛于一条路径。由上面的描述可知，维特比译码器至少需要完成以下操作：

·t时刻幸存路径度量的存储。

·t时刻到t+l时刻的分支度量的生成。

·t+1时刻幸存路径度量的生成和选择。

登录后复制

维特比译码器的基本结构正是按照这些操作划分的。前面说过，网格图是理解维特比算法的核心。其核心思想是依次在每个时刻对网格图相应列的每个点(对应于编码器该时刻的状态)，按照最大似然准则比较所有以它为终点的的路径，只保留一条具有最大似然值的路径，称之为幸存路径，而将其他路径堵死弃之不用，故到了下一时刻只要对幸存路径延伸出来的路径继续比较即可。即接收一段，计算、比较一段保留下幸存路径，如此反复直到最后。

登录后复制

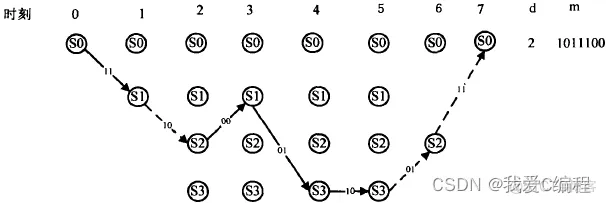
考虑Viterbi译码，假设卷积码的编码存储m只是个位数。在每一帧被接收时，译码器都必须更新状态，对于每一个状态，都有2k0条路径要估算。于是，译码器的计算量大致与成正比，等于。这是能够用此方式解码的码的约束长度的上限。这个限的大小取决于要求达到的比特率和技术水平，但是通常情况下，约束度N取7～9，这些值是目前典型的最大值。更长的约束长度也意味着功能更为强大的码，但只能在合理的码率下用其他技术来译码，例如序贯译码。

3.MATLAB核心程序

登录后复制

%采用BPSK调制
EsN0dB=EbN0dB-10*log10(R);
N0=10.^(-EsN0dB/10);
sigma=sqrt(N0);
plot_EbNo =-1:1:6;
Plot_Pe = [];
Plot_Pe2= [];
x_num=100000;
G=[1 1 1;1 0 1];
 
for k=1:length(N0)
    k
       x = bin_generator(x_num);
       x(find(x < 0)) = 0;
       x(find(x > 0)) = 1;
       
       %卷码编码
       s=encode(G,1,x);
       %BPSK经过AWGN信道
       r=(2*s-1)+sigma(k)*randn(1,length(s));
       r(2:10004)=0.25*r(1:10003)+0.75*r(2:10004);
       r(find(r < 0)) = 0;
       r(find(r > 0)) = 1;
       %译码
       dd=viterbi(G,1,r);
       r=(2*x-1)+sigma(k)*randn(1,length(x));
       r(2:10004)=0.25*r(1:10003)+0.75*r(2:10004);
       r(find(r < 0)) = 0;
       r(find(r > 0)) = 1;
       
       %误码计数
       Pe  = length(find(x - dd))/x_num;
       Pe2 = length(find(x - r))/x_num;
       Plot_Pe = [Plot_Pe Pe];
       Plot_Pe2= [Plot_Pe2 Pe2];
end
 
semilogy(plot_EbNo,Plot_Pe,'-bs',...
    'LineWidth',2,...
    'MarkerSize',8,...
    'MarkerEdgeColor','k',...
    'MarkerFaceColor',[0.0,0.9,0.0])
hold on
semilogy(plot_EbNo,Plot_Pe2,'-bo',...
    'LineWidth',2,...
    'MarkerSize',8,...
    'MarkerEdgeColor','k',...
    'MarkerFaceColor',[0.9,0.0,0.0])
grid;
xlabel('Eb/No (dB)')
ylabel('BER')
legend('通过维特比译码','不加编译码');

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删