SPA与积译码算法在LDPC误码率Matlab仿真中的应用

1.算法仿真效果

matlab2022a仿真结果如下：

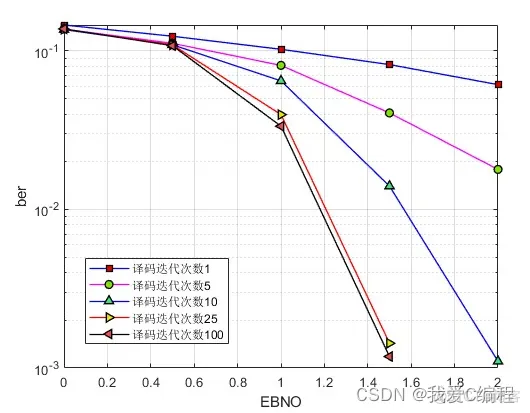
2.算法涉及理论知识概要

LDPC ( Low-density Parity-check，低密度奇偶校验）码是由 Gallager 在1963 年提出的一类具有稀疏校验矩阵的线性分组码 (linear block codes)，然而在接下来的 30 年来由于计算能力的不足，它一直被人们忽视。1996年，D MacKay、M Neal 等人对它重新进行了研究，发现 LDPC 码具有逼近香农极限的优异性能。并且具有译码复杂度低、可并行译码以及译码错误的可检测性等特点，从而成为了信道编码理论新的研究热点。

登录后复制

Mckay ，Luby 提出的非正则 LDPC 码将 LDPC 码的概念推广。非正则LDPC码 的性能不仅优于正则 LDPC 码，甚至还优于 Turbo 码的性能，是目前己知的最接近香农限的码。

在LDPC码的校验矩阵中，如果行列重量固定为(P，Y)，即每个校验节点有Y个变量节点参与校验，每个变量节点参与P个校验节点，我们称之为正则LDPC码。Gallager最初提出的Gallager码就具有这种性质。从编码二分图的角度来看，这种LDPC码的变量节点度数全部为P，而校验节点的度数都为Y。我们还可以适当放宽上述正则LDPC码的条件，行列重量的均值可以不是一个整数，但行列重量尽量服从均匀分布。另外为了保证LDPC码的二分图上不存在长度为4的圈。我们通常要求行与行以及列与列之间的交叠部分重量不超过1，所谓交叠部分即任意两列或两行的相同部分。我们可以将正则LDPC码校验矩阵H的特征概括如下：

1. H的每行行重固定为P，每列列重固定为Y。
2. 任意两行(列)之间同为1的列(行)数(称为重叠数)不超过1，即H矩阵中不含四角为1 的小方阵，也即无4线循环。
3. 行重P和列重Y相对于H的行数M、列数N很小，H是个稀疏矩阵。 登录后复制 在正则LDPC码的校验矩阵中。行重和列重的均值保持不变，所以校验矩阵中1的个数随着码长的增加而线性增长，整个校验矩阵的元素个数则成平方增长。当码长达到一定长度时，校验矩阵H是非常稀疏的低密度矩阵。对于正则的LDPC码，MacKay给出了以下两个结论：
4. 对于任意给定列重大于3的LDPC码，存在某个小于信道传输容量且大于零的速率r ，当码长足够长时，可以实现以小于r且不为零的速率无差错的传输。也就是说任意给定一个不为零的传输速率r，存在一个小于相应香农限的噪声门限，当信道噪声低于该门限且码长足够长的时候，可以实现以r速率无差错的传输。
5. 当LDPC码的校验矩阵H的列重Y不固定，而是根据信道特性和传输速率来确定时，则一定可以找到一个最佳码，实现在任意小于信道传输容量的速率下无差错的传输。 登录后复制 对LDPC码的定义都是在二元域基础上的，MaKcay对上述二元域的LDPC码又进行了推广。如果定义中的域不限于二元域就可以得到多元域GF(q)上的LDPC码。多元域上的LDPC码具有较二进制LDPC码更好的性能，而且实践表明在越大的域上构造的LDPC码，译码性能就越好，比如在GF(16)上构造的正则码性能己经和Turbo码相差无几。多元域LDPC码之所以拥有如此优异的性能，是因为它有比二元域LDPC码更重的列重，同时还有和二元域LDPC码相似的二分图结构。

码率是0.5，码长是2304，nb=24，kb=12，

基础矩阵为

3.MATLAB核心程序

登录后复制

[Rh,Ch] = size(H);
x        = [ones(1,Ch)];
EbN0     = [0:0.5:2];
 
 
Max_iter = 1;
 
 
for ij = 1:length(EbN0)
    for k = 1:100
    [k,ij]
    sigma = sqrt(1/(10^(EbN0(ij)/10)));
    %实际验证过程中，这个位置加入你的编码模块
    code  = (2*x-1);
    r     = code+randn(size(x))*sigma;
    %对应PPT公式
    Lv    = 2*r/(sigma^2);
    %SPA算法
    [ber,v1] = Sum_product_algorithm(Lv,H,Max_iter);
    %输入变量
    x(Rh+1:Ch);
    %输出变量
    v1(Rh+1:Ch);
    %计算错误数据
    err1(k,ij)=1-length(find(v1(Rh+1:Ch)==x(Rh+1:Ch)))/length(x(Rh+1:Ch));
    end
end
 
if Max_iter==1
   save R1.mat EbN0 err1
end
if Max_iter==5
   save R2.mat EbN0 err1
end
if Max_iter==10
   save R3.mat EbN0 err1
end
if Max_iter==25
   save R4.mat EbN0 err1
end
if Max_iter==100
   save R5.mat EbN0 err1
end
 
 
figure;
semilogy(EbN0,mean(err1,1),'b-o');
grid on
xlabel('EBNO');
ylabel('ber');

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删