神经网络主要由处理单元、网络拓扑结构、训练规则组成。处理单元是神经网络的基本操作单元,用以模拟人脑神经元的功能。一个处理单元有多个输入、输出,输入端模拟脑神经的树突功能,起信息传递作用;输出端模拟脑神经的轴突功能,将处理后的信息传给下一个处理单元,如图1所示。
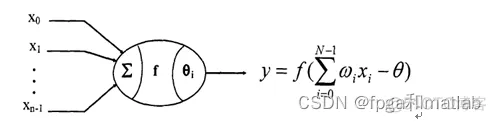
图1 神经网络基本处理单元
基本的神经处理单元其等效于人体的神经元,如图2所示,

图2 神经元和神经处理单元的对比
具有相同功能的处理单元构成处理层。常用的多层感知机由输入层、输出层和若干隐含层组成,神经网络的拓扑结构决定了各处理单元、各层之间信息的传递方式与途径。训练规则利用转换函数进行数据处理的加权及求和,训练网络系统进行模式识别,并将其转换成潜在的输出值。神经网络的基本出发点,就是通过简单函数的多次迭代,实现对复杂映射的拟合和逼近。神经网络能够实现一对一、一对多的映射关系。因此,许多实际问题都可以用神经网络模型来解决
住宅价格是住宅市场的核心,住宅市场的变化关系到广大消费者的切身利益,商品房价格是升是降,销售是冷是旺,是社会关注的热点问题。因此,从不同角度来看,对商品住宅价格的研究都存在着重要的理论与现实意义。商品住宅价格的变化受市场供求、人口、居民收入水平、经济政策等诸多因素的影响,其随时间变动的过程具有很大的不确定性,为较全面地刻画各方面对住房价格的影响,以把握未来住房价格的变动趋势,将通过神经元网络理论的预测方法,延伸应用于商品住宅价格的研究,对住宅价格进行科学的预测。
影响商品住宅价格变动的因素是复杂、多变的,将所有因素纳入分析研究是困难的。但是可以认为在一段经济、政治比较平稳时期,商品住宅价格的变动是由一些基本因素决定的。根据本文第二章介绍的,考虑到奥克兰地区的实际情况,将选取13个主要的因素作为影响房屋价格的主要因素:
·每个城镇的平均犯罪率;
·住宅用地超过500平米的比例;
·每个城镇非商业用地的比例;
·距离海洋的距离在1公里内,则为1,否则为0;
·氧化物浓度;
·每个房子的平均房间数;
·1940前自建房屋的比例;
·到购物中心的权值距离;
·高速公里的标号;
·每1万美元的管理费;
·教师比例;
·20岁以下的人口比例;
·退休人口比例。
将以上因素分别表示为:X1~X13。
clc;close all;clear all;warning off;%% Parameters initialization %load dataload data\housing_data.mat%Display the original data figure;subplot(4,4,1);plot(x(1,:));title('Per capita crime rate per town');subplot(4,4,2);plot(x(2,:));title('Proportion of residential land zoned for lots over 500m2');subplot(4,4,3);plot(x(3,:));title('Proportion of non-retail business acres per town');subplot(4,4,4);plot(x(4,:));title('1 within 1km from the sea, 0 otherwise');subplot(4,4,5);plot(x(5,:));title('Nitric oxides concentration (parts per 10 million)');subplot(4,4,6);plot(x(6,:));title('Average number of rooms per dwelling');subplot(4,4,7);plot(x(7,:));title('Proportion of owner-occupied units built prior to 1940');subplot(4,4,8);plot(x(8,:));title('Weighted distances to a main shopping center');subplot(4,4,9);plot(x(9,:));title('Index of accessibility to motorways');subplot(4,4,10);plot(x(10,:));title('Full-value of council rate per $10,000');subplot(4,4,11);plot(x(11,:));title('Pupil-teacher ratio by town');subplot(4,4,12);plot(x(12,:));title('Population below the age of 20');subplot(4,4,13);plot(x(13,:));title('Percentage of retirees');figure;plot(10000*t,'r');title('PRICE');grid on%% Select multiple data,train neural network %step1:parameternet = fitnet(10);net.trainParam.epcohs = 1000;%train timesnet.trainParam.goal = 0.0001;%aim error%step2:trainnet = train(net,x,t);%% By using the neural network to predict the price of housesview(net);y1 = net(x);%predict%% Shows the result figure;subplot(221);plot(t);title('Original price');axis([0,length(t),0,max(t)]);subplot(222);plot(y1);title('Predict prices ');axis([0,length(y1),0,max(y1)]);subplot(223);plot(y1);hold on;plot(t,'r');hold off;legend('Predict prices','Original price');title('Predict prices');axis([0,length(y1),0,max(y1)]);subplot(224);plot(y1 - t,'k');title('Prediction error ');figureplot(y1);hold on;plot(t,'r');hold off;legend('Predict prices','Original price');title('Predict prices');axis([0,length(y1),0,max(y1)]);figureplot(y1 - t,'k');grid on;title('Prediction error ');axis([0,length(y1),-50,50]);%save networkssave net.mat net1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.37.38.39.40.41.42.43.44.45.46.47.48.49.50.51.52.53.54.55.56.57.58.59.60.
load data\housing_data.mat”语句,可以将需要进行训练的函数调用到MATLAB的workspace中,方便数据的调用。
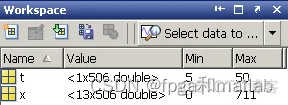
图1 数据调用
首先执行如下的MATLAB指令:
net = fitnet(10);
net.trainParam.epcohs = 1000;
net.trainParam.goal = 0.0001;
这里的主要含义就是使用fitnet函数产生一个随机的神经网络,然后将训练次数设置为1000,训练的误差目标设置为0.0001。随机产生的net其信息如下所示:
Neural Network
…………………………….
dimensions:
…………………………….
connections:
…………………………….
subobjects:
…………………………….
functions:
…………………………….
weight and bias values:
…………………………….
methods:
…………………………….
evaluate: outputs = net(inputs)
然后开始训练,执行如下的指令:
net= train(net,x,t);
训练完成后,系统会出现如下的神经网络界面:
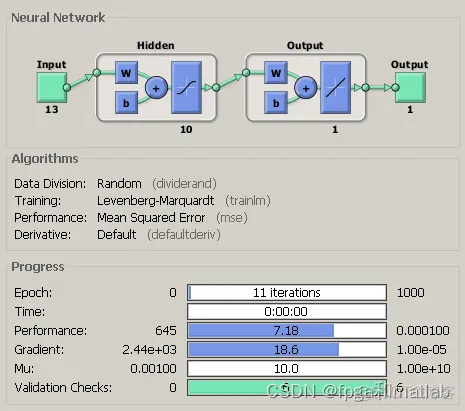
图2 神经网络界面
通过查看相关的信息,我们可以看到整个训练过程的性能如下所示:

图3 神经网络训练曲线
其训练误差分布如下所示:

图4 训练误差分布
从图4.4可知,通过神经网络训练后,多数数据可以分布在较小误差附近,个别数据会产生较大的误差。
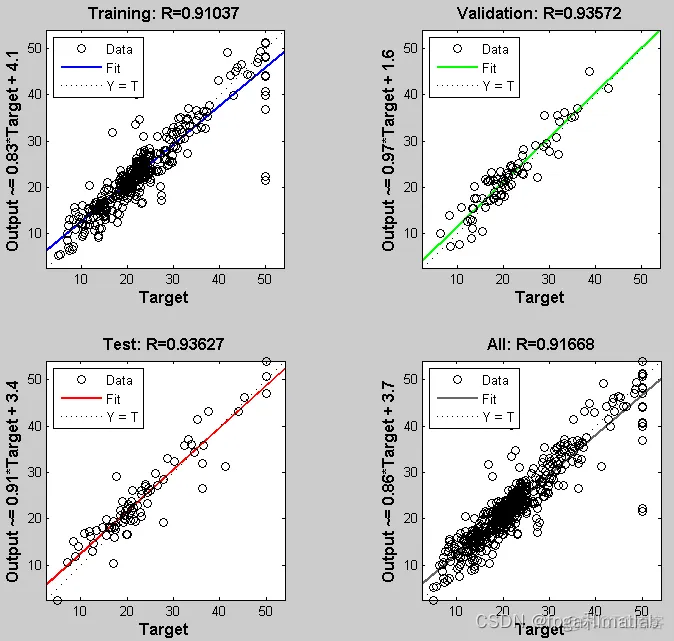
图5 数据分布
执行view,可以看到设计好的神经网络模型:
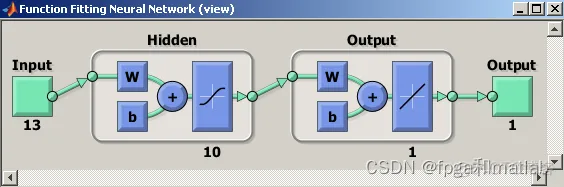
图4.6神经网络数据模型
最后使用设计得到的net函数进行数据的预测。
这里将原始的样本数据和通过神经网络预测得到的数据进行对比,其结果如下:
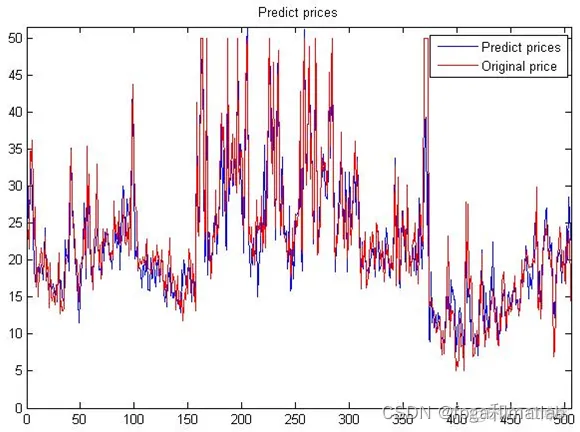
图7 原始样本数据和预测后的数据对比图
从图7可以看到,通过神经网络预测后的数据和原始的数据基本相似,通过相减得到其误差信息如下所示:
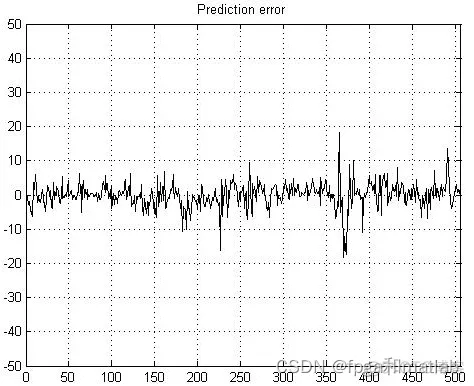
图8 误差曲线
从图8可知,通过神经网络之后,其预测输出值和样本值之间的误差都在0附近,但是对于部分值,如房屋价格中几个跳变的区域,误差较大,这就是对突发情况的预测能力较弱导致的。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删