【Lipschitz】基于matlab的Lipschitz李氏指数仿真

1.软件版本

MATLAB2013b

2.系统概述

Lipschitz exponent)，以德国数学家​ ​Rudolf Lipschitz​​命名，是一个描述比一般的连续可微更强的光滑性指数。具有一定条件的连续性称为李氏连续性。李氏指数α可用于描述信号的奇异性。一般来说，α越大，信号在该点就越光滑；α越小,则信号在该点的奇异性就越大。李氏指数是一个专用于描述函数光滑性的指数。一个函数如果存在无限次可导就称为光滑或没有奇异性，但它如果在某处有间断点或某阶导数不连续，通常叫做函数的奇异性，信号的奇异性通常用李氏指数来刻画。它与小波变换有着密切的关系，由小波变换描述信号奇异性的特点，我们不难得出，李氏指数也有描述奇异信号这一功能。李氏指数检测信号奇异性的结果简单明了，便于观察，具有很大的现实意义。

3.部分matlab程序

clc;clear;close all;warning off;addpath 'func\'%%%参数初始化Len         = 2048;%信号的长度Noise_Power = 0.5; %产生的测试的干扰大小select      = 2;   %选择信号%%%产生模拟的故障信号[s_normal,s_error] = func_sig_gen(Len,Noise_Power);figure;subplot(211);plot(s_normal);title('正常信号');subplot(212);plot(s_error);title('故障信号');%%%计算李氏指数if select == 1   signal = s_normal;endif select == 2   signal = s_error;end%多个尺度小波变换Ss      = 1;   Ls      = 32;wt      = CWT(signal,Ss:Ls,'gaus2');%模极大点Max_Pos = func_WMMT(wt,10);%将小波变化后的每一级的对应的最大值相连[Max_List,Ptr,Lengths] = func_find_Max_nlevel(Max_Pos,10); %画出模极大曲线figure;for k=1:length(Ptr)   vec = Max_List(:,Ptr(k):Ptr(k) + Lengths(k)-1);    plot(vec(2,:),log2(vec(1,:)));    hold on;endaxis([0,Len,0,6]);xlabel('u');ylabel('log2');%计算Lipschitz指数 Lipschitz = func_cal_Lipschitz(Ptr,Max_List,wt,Lengths); figure;plot(Lipschitz,'r');%%%根据李氏指数的计算结果对故障信号检测cnt = 0;PP  = [];for i = 1:length(Lipschitz)    if abs(Lipschitz(i)) >= 4       cnt = cnt + 1;        PP(cnt) = i;    endendif isempty(PP) == 0    START = min(PP);    ENDS  = max(PP);    figure;    plot(signal);title('故障检测');    hold on    plot(14*START,-10:0.1:10,'r');    hold on    plot(Len,-10:0.1:10,'r');else    figure;    plot(signal);title('无故障');    end1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.37.38.39.40.41.42.43.44.45.46.47.48.49.50.51.52.53.54.55.56.57.58.59.60.61.62.63.64.65.66.67.68.69.70.71.72.73.74.75.76.77.78.79.

4.部分仿真结论

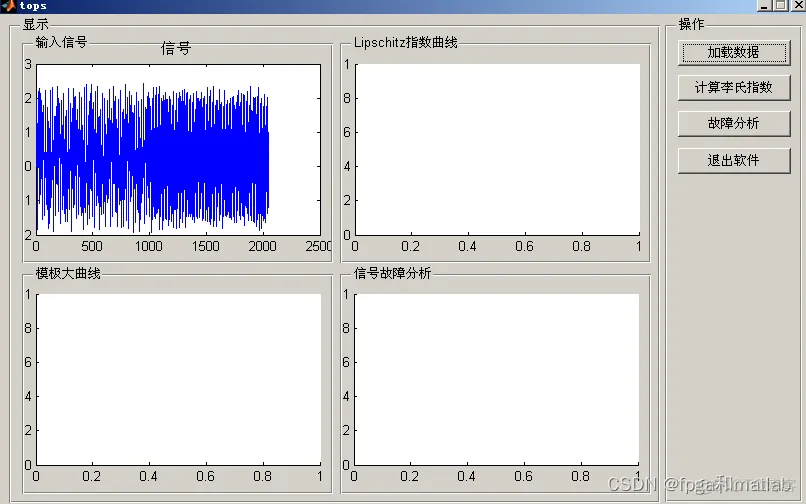
首先加载数据：

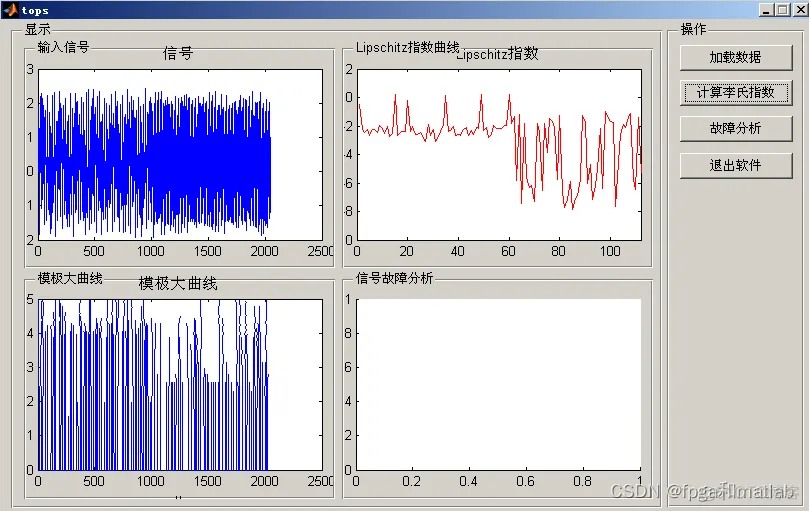
然后计算李氏指数：

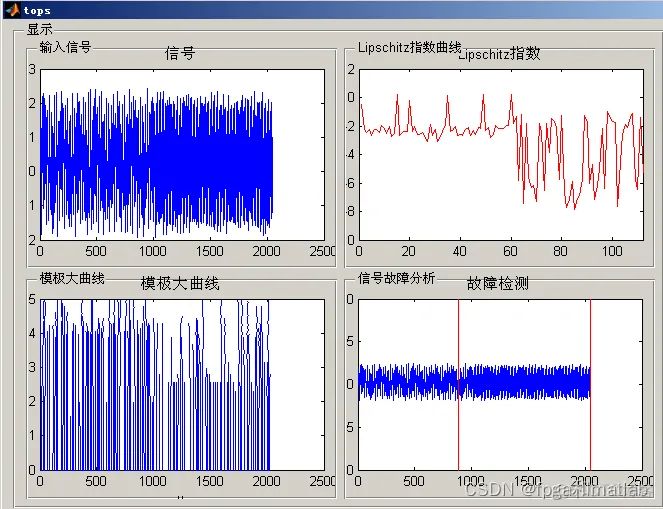
根据李氏指数进行故障检测分析：

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删