2PSK系统基于MATLAB的仿真分析

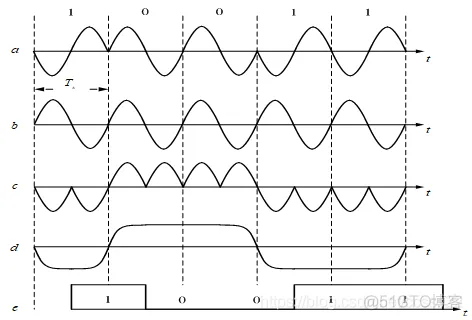
由于2PSK的幅度是恒定的，必须进行相干解调。经过带通滤波的信号在相乘器中与本地载波相乘，然后用低通滤波器滤除高频分量，在进行抽样判决。判决器是按极性来判决的。即正抽样值判为1，负抽样值判为0。2PSK信号的相干解调原理图如图2-4所示，各点的波形如图2-5所示。

由于2PSK信号的载波回复过程中存在着180°的相位模糊，即恢复的本地载波与所需相干载波可能相同，也可能相反，这种相位关系的不确定性将会造成解调出的数字基带信号与发送的基带信号正好相反，即“1”变成“0”吗“0”变成“1”，判决器输出数字信号全部出错。这种现象称为2PSK方式的“倒π”现象或“反相工作”。但在本次仿真中是直接给其同频同相的载波信号，所以不存在此问题。

基于matlab的2PSK的系统仿真_码元

登录后复制

% 2PSK调制解调程序及注释 clear all close all i=10; j=5000; fc=4; %载波频率 fm=i/5; %码元速率 B=2*fm; t=linspace(0,5,j); a=round(rand(1,i)); %随机序列,基带信号 figure(3); stem(a); st1=t; for n=1:10 if a(n)<1; for m=j/i*(n-1)+1:j/i*n st1(m)=0; end else for m=j/i*(n-1)+1:j/i*n st1(m)=1; end end end figure(1); subplot(411); plot(t,st1); title('基带信号st1'); axis([0,5,-1,2]); %由于PSK中的是双极性信号，因此对上面所求单极性信号取反来与之一起构成双极性码 st2=t; for k=1:j; if st1(k)>=1; st2(k)=0; else st2(k)=1; end end; subplot(412); plot(t,st2); title('基带信号反码st2'); axis([0,5,-1,2]); st3=st1-st2; subplot(413); plot(t,st3); title('双极性基带信号st3'); axis([0,5,-2,2]); s1=sin(2*pi*fc*t); subplot(414); plot(s1); title('载波信号s1'); e_psk=st3.*s1; figure(2); subplot(511); plot(t,e_psk); title('e_2psk'); noise=rand(1,j); psk=e_psk+noise; %加入噪声 subplot(512); plot(t,psk); title('加噪后波形'); psk=psk.*s1; %与载波相乘 subplot(513); plot(t,psk); title('与载波s1相乘后波形'); [f,af] = T2F(t,psk); %通过低通滤波器 [t,psk] = lpf(f,af,B); subplot(514); plot(t,psk); title('低通滤波后波形'); for m=0:i-1; if psk(1,m*500+250)<0; for j=m*500+1:(m+1)*500; psk(1,j)=0; end else for j=m*500+1:(m+1)*500; psk(1,j)=1; end end end subplot(515); plot(t,psk); axis([0,5,-1,2]); title('抽样判决后波形')1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.37.38.39.40.41.42.43.44.45.46.47.48.49.50.51.52.53.54.55.56.57.58.59.60.61.62.63.64.65.66.67.68.69.70.71.72.73.74.75.76.77.78.79.80.81.82.83.84.85.