matlab2013b


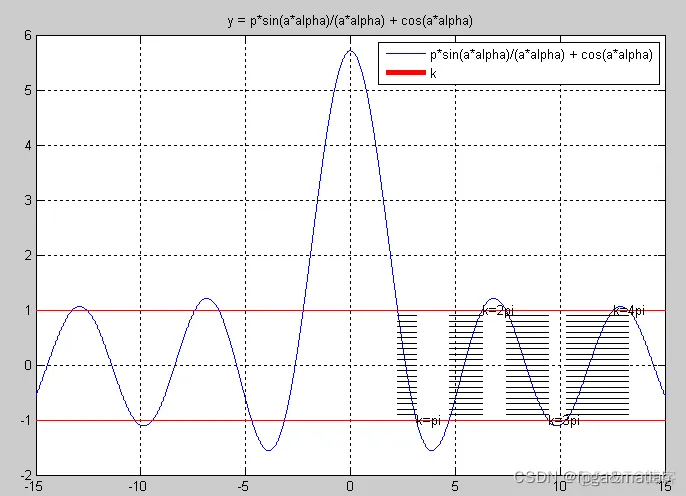
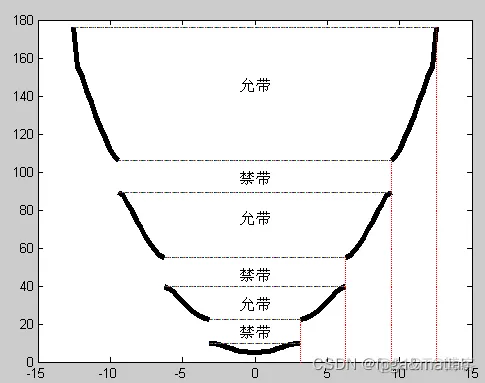
clc;clear;close all;figurep = 3*pi/2;a = 1;alpha = -15:0.0005:15;index = 1;for i=1:length(alpha) if abs(alpha(i))<0.001 y(i) = p + 1; else y(i) = p*sin(a*alpha(i))/(a*alpha(i)) + cos(a*alpha(i)); end endplot(alpha,y,'b');hold on;plot(-15:0.01:15,1,'r-','LineWidth',4);hold on;plot(-15:0.01:15,-1,'r-','LineWidth',4);hold on;title('y = p*sin(a*alpha)/(a*alpha) + cos(a*alpha)');figure_s();hold off;%******注意通过以下代码求出图像中的填充区域*******%四个区间:%A:2.2540 - 3.1480%B:4.7206 - 6.2965%C:7.4290 - 9.4450%D:10.3040- 13.2755 % startpoint = 2.2540;% endpoint = 3.1480;% N = 10000;% k = 0;% alpha2 = solvealpha(startpoint,endpoint,N,k);% alpha2%******注意通过以上代码求出图像中的填充区域*******legend('p*sin(a*alpha)/(a*alpha) + cos(a*alpha)','k');text(pi, -1,'k=pi');text(2*pi, 1,'k=2pi');text(3*pi,-1,'k=3pi');text(4*pi, 1,'k=4pi');grid on;figure%使用四个区间的平方,作为图2的y轴区间%使用四个区间的平方,作为图2的y轴区间%使用四个区间的平方,作为图2的y轴区间%AAAAstartpoint = 2.2540;endpoint = 3.1480;N = 10000;k = -pi:(2*pi)/20:pi;for i = 1:length(k)alpha2(i) = solvealpha(startpoint,endpoint,N,k(i));alpha2(i) = alpha2(i)*alpha2(i);endplot(k,alpha2,'k','LineWidth',4);hold on;plot(-pi:(2*pi)/80:pi,alpha2(length(alpha2)));hold on;clear kclear alpha2%BBBBstartpoint = 4.7206;endpoint = 6.2965;N = 10000;k = -2*pi:(2*pi)/20:-1*pi;for i = 1:length(k)alpha2(i) = solvealpha(startpoint,endpoint,N,k(i));alpha2(i) = alpha2(i)*alpha2(i);endplot(k,alpha2,'k','LineWidth',4);hold on;k = pi:(2*pi)/20:2*pi;for i = 1:length(k)alpha2(i) = solvealpha(startpoint,endpoint,N,k(i));alpha2(i) = alpha2(i)*alpha2(i);endplot(k,alpha2,'k','LineWidth',4);hold on;plot(-1*pi:(2*pi)/80:1*pi,alpha2(1));hold on;plot(-2*pi:(2*pi)/80:2*pi,alpha2(length(alpha2)));hold on;clear kclear alpha2%CCCCstartpoint = 7.4290;endpoint = 9.4450;N = 10000;k = -3*pi:(2*pi)/20:-2*pi;for i = 1:length(k)alpha2(i) = solvealpha(startpoint,endpoint,N,k(i));alpha2(i) = alpha2(i)*alpha2(i);endplot(k,alpha2,'k','LineWidth',4);hold on;k = 2*pi:(2*pi)/20:3*pi;for i = 1:length(k)alpha2(i) = solvealpha(startpoint,endpoint,N,k(i));alpha2(i) = alpha2(i)*alpha2(i);endplot(k,alpha2,'k','LineWidth',4);hold on;plot(-2*pi:(2*pi)/80:2*pi,alpha2(1));hold on;plot(-3*pi:(2*pi)/80:3*pi,alpha2(length(alpha2)));hold on;clear kclear alpha2%DDDDstartpoint = 10.3040;endpoint = 13.2755;N = 10000;k = -4*pi:(2*pi)/20:-3*pi;for i = 1:length(k)alpha2(i) = solvealpha(startpoint,endpoint,N,k(i));alpha2(i) = alpha2(i)*alpha2(i);endplot(k,alpha2,'k','LineWidth',4);hold on;k = 3*pi:(2*pi)/20:4*pi;for i = 1:length(k)alpha2(i) = solvealpha(startpoint,endpoint,N,k(i));alpha2(i) = alpha2(i)*alpha2(i);endplot(k,alpha2,'k','LineWidth',4);hold on;plot(-3*pi:(2*pi)/80:3*pi,alpha2(1));hold on;plot(-4*pi:(2*pi)/80:4*pi,alpha2(length(alpha2)));hold on;clear kclear alpha2%画虚线plot(pi, 0:4.7206^2,'r');hold on;plot(2*pi,0:7.4290^2,'r');hold on;plot(3*pi,0:10.3040^2,'r');hold on;plot(4*pi,0:13.2755^2,'r');hold on;text(-1, 145,'允带');text(-1, 96,'禁带');text(-1, 75,'允带');text(-1, 45,'禁带');text(-1, 30,'允带');text(-1, 15,'禁带');1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.37.38.39.40.41.42.43.44.45.46.47.48.49.50.51.52.53.54.55.56.57.58.59.60.61.62.63.64.65.66.67.68.69.70.71.72.73.74.75.76.77.78.79.80.81.82.83.84.85.86.87.88.89.90.91.92.93.94.95.96.97.98.99.100.101.102.103.104.105.106.107.108.109.110.111.112.113.114.115.116.117.118.119.120.121.122.123.124.125.126.127.128.129.130.131.132.133.134.135.136.137.138.139.140.141.
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删