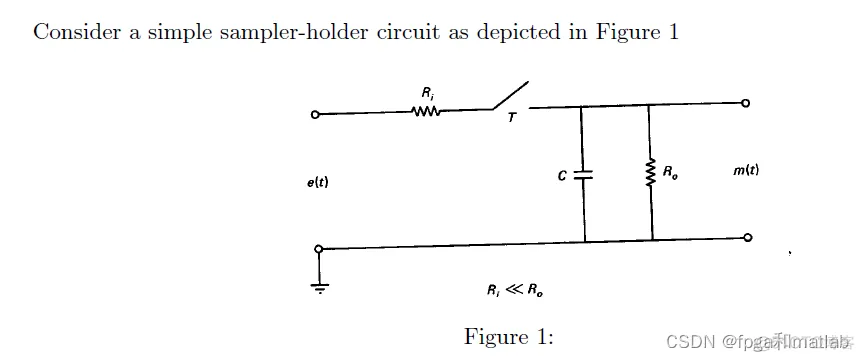
考虑一个简单的采样保持器电路,如图1所示,其中R0远大于Ri。开关周期为T,然后假设采样是在开关闭合的时候立刻完成的,然后也是快速的打开。因此,输入信号e(t)采样后可以得到e(kT)。信号e(KT),进行电路分析,计算一个采样周期T,t(KT,(K+1)t)的响应函数m(t)。描述一下这响应曲线,然后分析这个电路的阶数。分析电容C式怎么影响这个保持器的结果的。如果RI和RO都为10欧姆,C是0.1F,1F,10F,然后T分别设置为1s和2s,画出m,然后分析结论。
根据电路系统的相关原理可知,信号通过该电路之后,得到信号满足如下的关系式:
根据问题一的要求,我们首先对电路进行理论上的分析。
根据电流守恒公式,可以列出如下的微分方程式:
由于C和R0是并联结构,所以两个电路支路电压都可认为是。那么根据电流守恒(输入=输出)我们可以得到如下的守恒公式:
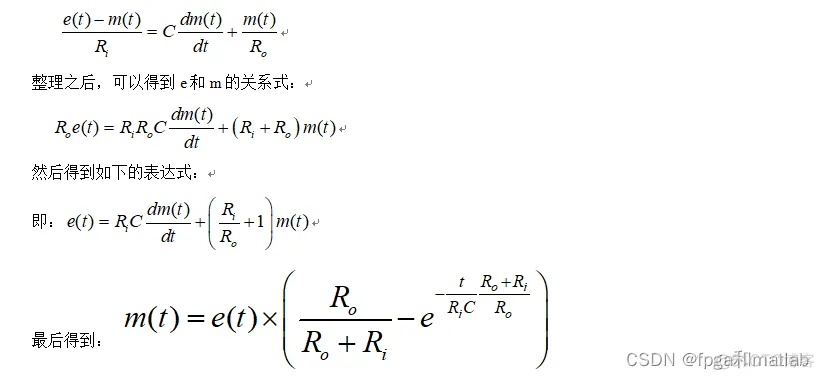

matlab仿真程序1:
clc;clear;close all;warning off;Ri = 10;Ro = 10;N = 300;%设置输入信号的是一个阶跃信号for k = [1:1:N] e(k) = 10;end%T=1,C=0.1C = 0.1;T = 1;for k = [1:1:N] m(k) = e(k)*( Ro/(Ro+Ri) - exp( -(Ro+Ri)*k*T/(Ro*Ri*C) ) ); endfigure(1)plot([1:1:N],m,'g-','linewidth',2);%T=1,C=1C = 1;T = 1;for k = [1:1:N] m(k) = e(k)*( Ro/(Ro+Ri) - exp( -(Ro+Ri)*k*T/(Ro*Ri*C) ) ); endhold onplot([1:1:N],m,'y-','linewidth',2);%T=1,C=10C = 10;T = 1;for k = [1:1:N] m(k) = e(k)*( Ro/(Ro+Ri) - exp( -(Ro+Ri)*k*T/(Ro*Ri*C) ) ); endhold onplot([1:1:N],m,'m-','linewidth',2);%T=2,C=0.1C = 0.1;T = 2;for k = [1:1:N] m(k) = e(k)*( Ro/(Ro+Ri) - exp( -(Ro+Ri)*k*T/(Ro*Ri*C) ) ); endfigure(1)plot([1:1:N],m,'b-','linewidth',2);%T=2,C=1C = 1;T = 2;for k = [1:1:N] m(k) = e(k)*( Ro/(Ro+Ri) - exp( -(Ro+Ri)*k*T/(Ro*Ri*C) ) ); endhold onplot([1:1:N],m,'r-','linewidth',2);%T=2,C=10C = 10;T = 2;for k = [1:1:N] m(k) = e(k)*( Ro/(Ro+Ri) - exp( -(Ro+Ri)*k*T/(Ro*Ri*C) ) ); endhold onplot([1:1:N],m,'k-','linewidth',2);grid on;legend('T=1,C=0.1','T=1,C=1','T=1,C=10','T=2,C=0.1','T=2,C=1','T=2,C=10');xlabel('Sample Times(s)');ylabel('m(t)');axis([0,N,-5,6]);1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.37.38.39.40.41.42.43.44.45.46.47.48.49.50.51.52.53.54.55.56.57.58.59.60.61.62.63.64.65.66.67.68.69.70.71.72.
仿真结果如下:
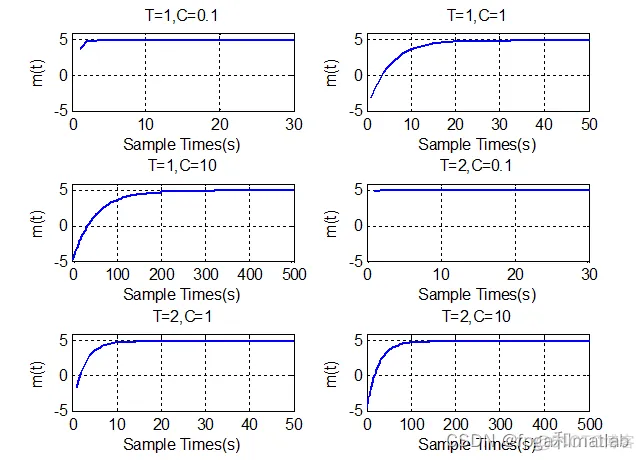
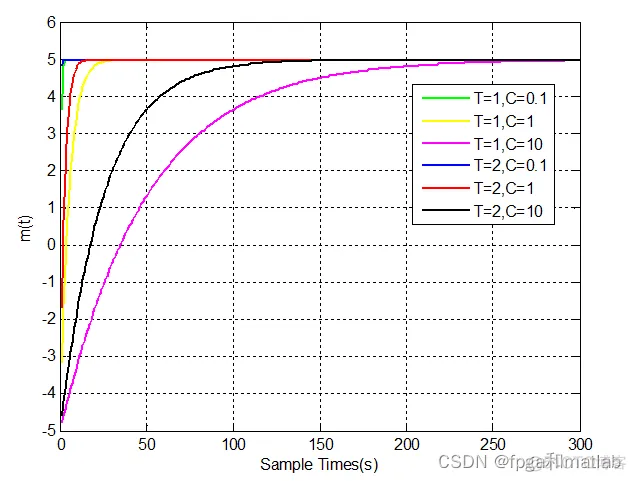
从上面的仿真结果可知,
当T不变的时候,C从小变大的时候,m(t)的的响应时间越长。
当C固定,改变时间T的时候,当T越大,m(t)的的响应速度越快。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删