本文利用MSC.Nastran有限元分析软件和MSC.Patran前后处理软件,微型货车车身进行了FEA建模,并进行了车身模态的理论计算分析,理论模态分析结果与试验模态分析结果进行了对比,对比结果证明了理论分析和试验分析的一致性非常好,这说明了此部分的分析工作完全可以利用计算机来代替试验室的大量同类试验工作,并且可以在还没有设计样车的设计过程中进行。
前言
在汽车产品设计中,预先掌握所设计产品的动态特性,从动态角度对产品进行设计,使所设计的产品满足动态要求,是非常重要的。获得产品结构的固有振动频率和振型,可以从两个方面得到,一种方法是通过对实际样车进行试验,识别出结构的各阶模态频率和振型,另一种方法是通过理论分析计算,分析计算出结构的各阶模态和振型。试验方法的局限性是必须在设计样车制造出来之后,才能进行试验分析,通过对实际样车的试验分析,得出产品的基本动态特性,再返回去修改设计,通过几轮样车制造和大量的试验分析,最终也能得到一个较为满意的产品,但周期长费用高。理论计算分析方法可以在没有实际样车而只有设计结构的情况下,得出所设计产品的各阶模态,预测出产品的动态特性,从而能减少样车的制造次数与试验次数,节省开发费用和缩短开发周期。
由于汽车车身结构是一个非常复杂的板壳结构,不可能应用简单的力学公式直接计算,而必须把其结构离散化,利用有限元方法的计算分析,才能得出结果分析结果。
本文利用有限元方法,采用MSC.Patran软件离散并建立了微型货车车身(以下称为白车身)的有限元模型,利用MSC.Nastran求解该模型,得出了白车身的各阶自由振动频率和振型,并和试验模态进行了对比。
几何模型和有限元模型
2.1几何模型
在建立白车身的几何模型时,直接利用CAD的设计数据,并根据FEM计算的需要和要求,进行必要的简化之后而得到。由于车身CAD设计的特点,在部分零件的3D数据之间,存在用于让位的料缝缝隙,对于料缝缝隙,进行了几何上的协调。建立几何模型时,忽略车身上用于装配其他部件的螺钉、螺母、零件中面与面之间的较小的倒圆和倒棱以及对力学结构影响较小的一些冲压筋、孔和一些工艺结构,忽略车身中非重要结构的小零件。对重要零件进行简化时,尽量保持和原始CAD设计的结构一致,在结构上简化较少,以便真实反映零件的结构特征。
由于车身在结构上是由多个零件组成的,在建立几何模型时,根据零件名称建立零件组,每一个组中放一个零件。经过简化和进行合理的省略之后,该白车身由45个对称零件,21个非对称零件和7根钢管横梁,总计118个零件经焊接组装而成。因此在建立几何模型时,划分了70个零件组来分别存放这118个零件,得到零件独立的几何模型。
2.2 有限元模型
由于微型汽车车身主要是由钣金冲压件和等半径等厚度的钢管横梁经过点焊和CO2保护焊焊接后组成,因此用壳体单元Quard4和部分Tria3来模拟车身零件的薄板钣金结构和横梁的钢管结构。
在建立车身的几何模型时,需要点焊的地方,加上硬点,点焊焊点采用两种方式处理:①几何上完全协调,消除了料缝的地方,使两个零件相同位置硬点处的两个节点同节点化,使之连为一体;②部分有料缝的地方,采用MPC连接两个硬点处的节点。CO2保护焊缝用MPC连接相应位置处的节点来模拟CO2焊缝。
完成后的有限元模型规模:单元数190662,MPC数 310,节点数192868。
3分析结果
3.1 理论计算分析结果和试验分析结果
理论和试验模态分析仅考虑了白车身自身的质量和刚度,分析计算了白车身的自然模态频率和振型。理论分析频率范围为0~80Hz, 试验分析频率范围为0~100Hz,各阶模态的理论和试验分析结果如表1所示。
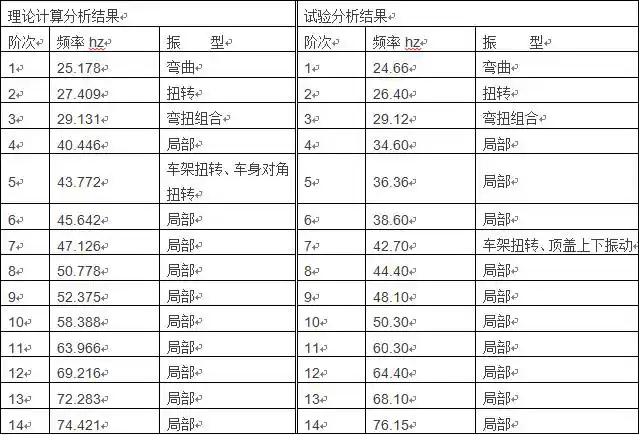
表1 白车身模态的理论计算和试验分析结果
3.2 主要振型图
白车身有限元理论模态分析结果的前几阶模态振型图,如图1~4所示。

图1 一阶模态振型(纵向弯曲)

图2 二阶模态振型(扭转)

图3 三阶模态振型(横向弯曲和扭转组合)

图4 五阶模态振型
4.分析结果讨论
4.1 有限元模型精度验证
有限元模型必须有较高精度,这样其分析结果才是可信的,其分析结论才能在产品设计中实际使用。从表1的理论和试验分析结果可知,理论和试验分析的前三阶模态是非常一致的,其前3阶模态的对比分析结果如表2所示。

表2 前3阶模态对比
在4阶以上模态,分析表1的计算和试验结果,可以发现在阶次错位的情况下,其频率和振型是一致的,即理论模态的第5阶以后和试验模态的第7阶以后,各阶模态在频率和振型上是一致的。
理论分析在30~40Hz段没有模态,试验分析在该段有2个局部模态,其原因有两方面,其一是模型的简化造成局部模态的改变;其二是试验误差和数据处理误差造成的虚假局部模态。而有限元模型建立时,对其结构未作大的简化,分析方法采用的是LANCZOS算法,这基本可以判断理论计算的结果是可信的,试验时在30~40Hz段出现的局部模态是试验误差和数据理误差造成的。去掉这两个局部模态,则理论和试验是基本一致的,并且计算精度较高。
4.2 模型规模和计算精度
有限元模型必须具备一定的规模,其计算结果才有较高的分析计算精度,本文对白车身的模态分析应用了两各不同规模的有限元模型进行了分析。其结果如表3所示。
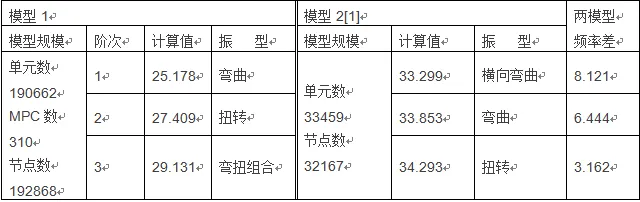
表3 不同规模模型计算结果(Hz)
☆模型1是本次计算分析所用模型,分析软件是MSC.Nastran;模型2使用的分析软件是ANSYS。
从表3可以看出,对同一辆车,由于建模时简化规模不同,其有限元模型的规模是不一样的,其计算结果也有较大的差别,表2和表3的数据表明,要获得高精度的计算结果,计算模型必须具备一定的规模,规模较小时计算误差较大。
4.3 车身结构的动态分析
汽车行驶时要承受各种来自外界和内部激励源的激励,其中主要的激励来自路面对车轮的冲击和发动机的振动,研究汽车的动态特性,能有效地分析其舒适性和疲劳寿命。设计汽车时,车身的固有频率必须要有效地避开其激励频率,防止其发生共振。分析汽车的动态特性时,最好用整车的固有频率来分析,白车身的固有频率不是严格意义上的整车固有频率,但比较接近,当在白车身模型上加上货厢、发动机、前桥固定横梁等其他部分时,汽车的整车固有频率将会略为提高。
汽车在激励作用下,其振动是各阶模态振动的综合反映,起主要作用的是前几阶的整体模态,因此应着重分析前几阶频率。
根据相关文献,当汽车在正常路面上以低于150km/h的速度行驶时,路面对汽车的激励频率低于21Hz,所以汽车车身的第一阶固有频率应高于21Hz,以不低于25Hz为好。根据上述结果分析,地面的激励将不会使整车发生共振。
白车身的整体模态频率分别是25.178Hz、27.409Hz、29.131Hz、43.772Hz,其他模态是局部模态,局部模态是结构的局部振动,一般不会严重影响的使用。
汽车在怠速、正常行驶和加速行驶时,发动机的转速不一样,其对汽车的激励频率也不一样。被分析车辆使用发动机的基本转速参数为:①怠速850±50 r/min;②额定功率5300±50 r/min,因此发动机对汽车的激励频率为:
怠速时激振频率:f=(850±50)/60×2=28.33±1.67 Hz。
正常行驶时激振频率:f=(5300±50)/60×2=176.67±1.67 Hz。
正常行驶时,发动机的激振频率已经远大于汽车的整体模态频率,不会引起汽车的共振。但怠速时,发动机激振频率和白车身主要的前三阶整体模态频率非常接近,即使整车的整体固有频率比白车身的整体固有频率略微提高,在怠速时也很容易引起车身的共振,影响舒适性与汽车的疲劳寿命。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删