文中以某公司新型注吹机上模板为研究对象,利用SolidWorks和HyperWorks分别进行三维参数化建模与力学性能分析,并运用有限元中的优化模块对上模板进行结构优化设计,并根据拓扑优化分析结果、模板的设计要求和制造工艺要求,获得了拓扑优化后的模板结构。经公司生产实践,该模板结构达到设计要求,结构合理,很好地解决了工程中的实际问题。
1)静力学分析
根据材料力学弯曲强度理论公式,并结合注吹机安装尺寸和设计要求,初步确定上模板的外形尺寸:长度为1632mm,宽度为240mm,初始高度为300mm。其外形如图1所示。
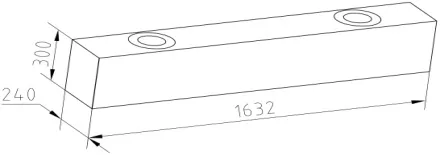

图1上模板的外形图
将升降导杆简化为刚性体,与上模板的连接看成是刚性连接;在模板的对称面上施加对称约束;在安装注芯主板位置处添加对上模板的Z方向的位移约束。
液压缸合模力是通过螺栓作用于上模板,因此,可将每个螺栓孔看成一个节点,即共有10个节点,其合模力简化为作用于上述节点的均布载荷。上模板添加的边界条件及载荷情况如图2所示。
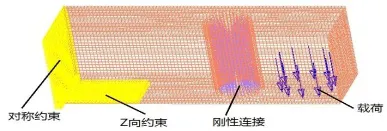
图2 上模板的边界条件与载荷
由应力云图可看出,上模板的应力大部分都在30.0MPa以下,受力情况较均匀,整体应力值很小,最大应力位于螺栓节点处,为95.1MPa,可见该模板应力裕度很大。从位移云图可以看出,总体趋势为离模板中心越远,上模板的变形量就越大,最大变形量约为0.098mm,根据设计要求其变形量最大为0.3mm,同样其变形量裕度过大。
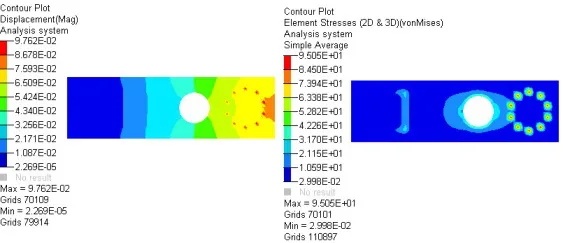
图 3上模板位移和应力云图
2)建立拓扑优化模型
模板优化模型与之前的有限元分析模型的建模过程相似,网格划分、边界条件与载荷的添加一样,不同的是,拓扑优化需选取整体模型作为优化对象,因此并不需要设置对称约束。同时,在优化前要将模板结构划分出设计区域和非设计区域,其中,对于在优化设计时不允许改变的区域,如导孔、载荷和约束区域等,将其划分为非设计区域,其余为设计区域。然后再进行网格划分,得出优化模型如图4所示。
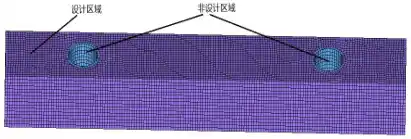
图4 上模板拓扑优化的有限元模型
3)定义优化数学模型
根据模板拓扑优化数学模型,定义其设计变量,约束函数及其目标函数。
| 目标函数 | 模板的体积分数最小 |
| 约束函数 | 左右两端节点的变形量最大为0.3mm |
| 设计变量 | 体积分数 |
4)分析拓扑优化结果
优化分析结束后,进入到Hyperview后处理中查看优化结果,得到经过60步迭代,伪密度云值为0.3~1的密度云图,如图5所示。
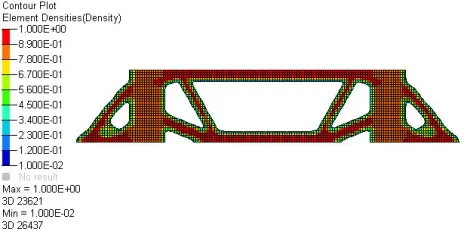
图5上模板拓扑优化结果
5)二次建模及静力学分析
基于拓扑优化所得到的优化结果,结构边界呈现不规则性,直接由优化结果建立CAD模型是行不通的,需要对优化结果进行适当的简化和修改。依据拓扑优化结果中伪密度云图的大致结构,保留结构受力的主要路径,结合经验对结构进行重新设计,在设计过程中对拓扑优化结构进行一定的调整,可用近似的规则形状代替不规则形状。在SolidWorks中建立优化设计后的实体模型,其模型如图6所示。

图6优化后上模板实体模型
二次分析得到模型的应力云图和位移云图如图7所示。
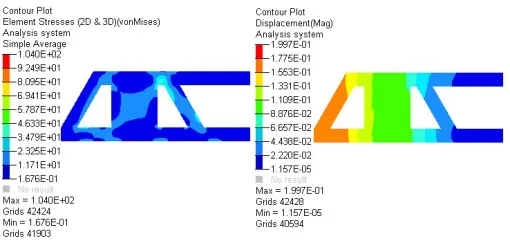
图7优化后上模板应力和位移云图
从图中可知,优化后的上模板最大应力为104MPa,最大变形量为0.200mm,其强度和刚度都能满足要求。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删