OptiStruct有轨电车铰接安装座优化设计实践

摘  要：

有轨电车各车体模块间通过铰接结构组合约束、释放自由度，使车辆能够平顺通过小半径曲线，保证车辆平稳运行。铰接结构受力复杂，频繁承受动态载荷，因此铰接安装座是有轨电车车辆的关键部件。有轨电车车辆开放铰安装座的最初设计由板材拼焊组成，工艺复杂，其焊接质量、安装面平面度等关键尺寸很难保证。本文利用OptiStruct 软件的拓扑优化功能对铰接安装座进行优化分析与设计，根据优化结果并结合铸造工艺要求，形成铸钢安装座的最优设计，并通过有限元分析计算的验证，满足工况载荷要求。

关键字：拓扑优化 有轨电车 铰接 强度分析

0 概述

随着城市规模的不断扩大，公共交通成为交通行业发展的重点[1]。载客量大、乘坐方便的有轨电车成为了中小城市干线交通和大城市支线交通的首选[2]。现代有轨电车大都采用短车体模块化设计，各车体模块间通过铰接结构组合约束、释放自由度，使车辆能够平顺通过小半径曲线，保证车辆平稳运行。铰接结构受力复杂，频繁承受动态载荷，因此铰接安装座是有轨电车车辆的关键部件。有轨电车车辆开放铰安装座的最初设计由板材拼焊组成，工艺复杂，其焊接质量、安装面平面度等关键尺寸很难保证。

本文以优化设计理论为基础，设计一种铸钢开放铰机构安装座。本文首先将铰接安装座可设计空间进行有限元建模，其次建立约束方程和目标函数进行优化分析，最终根据优化结果分析设计出刚度好、可维护性好、轻量化的铸钢安装座。即在给定的设计空间内找到最优的材料分布。

图1 优化前铰接安装座

1  拓扑优化理论基础

结构拓扑优化能在工程结构设计的初始阶段为设计者提供一个概念性设计，使结构在布局上能够采用最优方案，已经成为当今研究结构优化设计的一个热点。OptiStruct是一个面向产品设计、分析和优化的有限元和结构优化求解器，拥有先进的优化技术，提供全面的优化方法。

变密度法是连续体拓扑优化的常用方法，是一种比较流行的力学建模方式，与采用尺寸变量相比，它更能反应拓扑优化的本质特征。它也正是OptiStruct中所采用的材料插值方法。变密度法的基本思想是引入0到1的可变材料，指定每个有限单元的密度相同，并以每个单元的相对密度为设计变量。当单元相对密度t=0时，表示该单元无材料，单元应删除；当单元相对密度t=l时，表示该单元有材料，保留或增加该单元。变密度法直接假定相对密度与材料弹性模量之间的非线性对应关系。以结构整体的体积约束作为优化的约束条件，以刚度最大化作为优化的目标函数。

2 有限元模型

本次分析设计与最初设计的结构比较，在材质、结构类型上完全不同，铰接安装座与车体型材间通过铆接连接，因此要预留安装空间，安装座与铰接机构的接口结构保留不变。在确定了铰接安装座设计空间后，运用拓扑优化变密度法对该空间进行结构优化。

本文根据有轨电车的实际运行状态设计了两种工况，工况一由有轨电车开放铰在实际运营中所受到的最大静态力进行加载，工况二由有轨电车整车工况计算出的最大铰接力得出。该模型对预测的螺栓孔位置进行约束。共划分了46448个节点，43135个单元。

表 1 开放铰安装座载荷工况

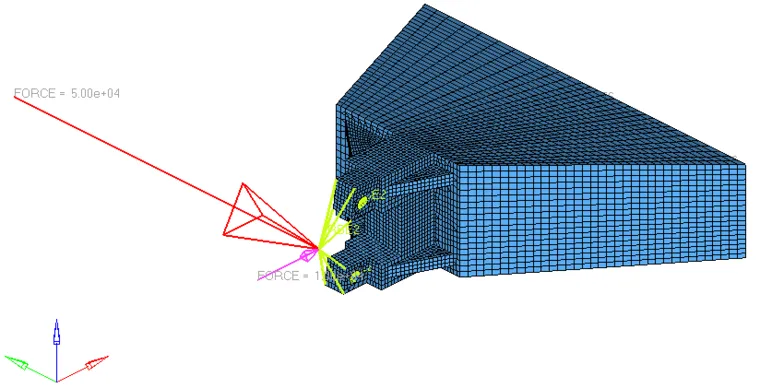
图2铰接安装座有限元模型

3 优化结果分析

在hyperworks的optimization模块建立拓扑优化的设计变量，并定义相应函数：体积(volume)。以体积最小作为优化目标，施加载荷节点合位移小于0.05，设计变量为单元密度。安装孔以此建立优化模型进行优化分析，优化得到的结构不仅重量最轻，而且满足所有载荷工况的约束要求。本次分析包含了两种响应，体积响应和位移响应。

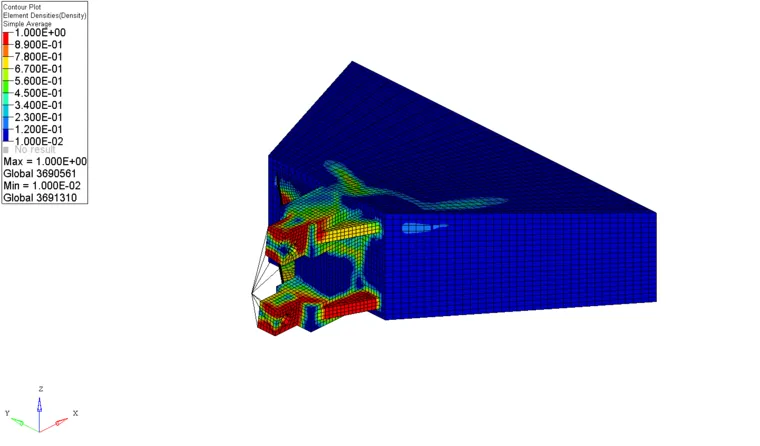
图3 铰接安装座单元密度

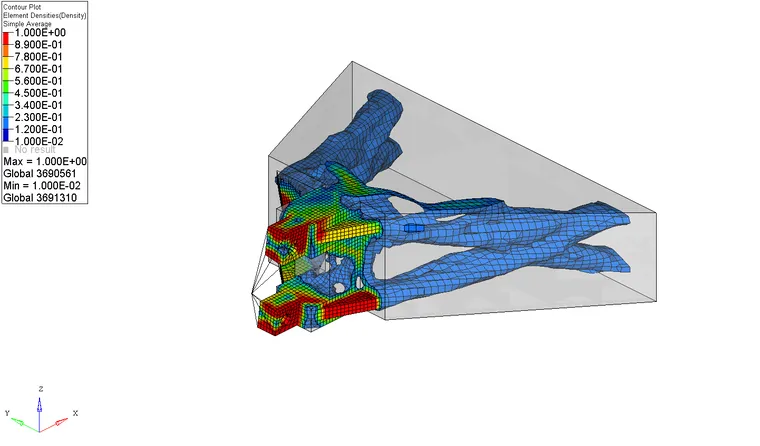
图4铰接安装座拓扑结果

运行OptiStruct 软件，进行优化分析，最终得到最优结果，优化结果见图3、图4 所示，优化结果保留了螺栓约束部位、铸件安装头及中间筋状的部分材料。因此在理论上，该铰接安装座有较大的余量可以进行优化。但是考虑到铰接安装座的安装，以优化结果作为基础，结合铸造工艺，重新设计铰接安装座，设计模型见图5。

图5 三维模型

4 优化后结构校核

在HyperMesh 中重新建立新设计的开放铰安装座的有限元模型，使用Nastran求解器重新校核上述两个工况，50KN 的横向工况最大应力为278MPa，1KN 的压缩工况最大应力为66MPa，两个工况的最大应力都处在安装底座与筋板交界处。均低于355钢允许的最小屈服强度，符合设计要求。图5 给出了50KN 横向最大静态力工况的应力云图。

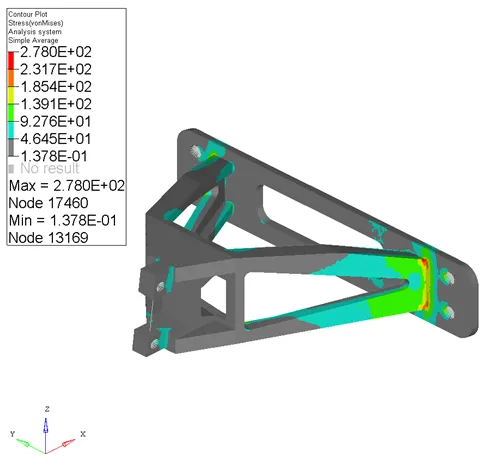
图6 应力结果云图

5结论

本文根据低地板车辆上铰接安装座受力与安装情况建立拓扑优化模型，并最终设计出满足强度与结构要求的铸钢安装座。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删