HyperWorks发动机支架拓扑优化：性能与重量的完美平衡

1 引言

结构拓扑优化又称结构布局优化，是一种根据载荷、约束及优化目标寻求结构材料最佳分配的优化方法。

结构优化设计的目的在于寻求既安全又经济的结构形式，根据结构的类型和形式、工况、材料和规范所规定的各种约束条件(如强度、刚度、稳定、构造要求等)，提出优化的数学模型(目标函数、约束条件、设计变量)，然后根据优化设计理论和方法求解优化模型，以获得最佳的静力或动力等性态特征。

结构优化设计集计算力学、数学规划、计算机科学以及其他工程学科于一体，是一综合性、实用性很强的理论和技术，是近代设计方法的重要内容之一。目前结构优化设计应用的领域涉及航空航天、机械、土木、水利、桥梁、汽车、铁路等诸多领域，解决的问题从减轻结构重量扩展到降低应力水平、改进结构性能和提高安全寿命等诸多方面［1］。

结构优化方法主要是尺寸优化、形状优化和拓扑优化。

拓扑优化在工程设计初始阶段为设计者提供概念性设计，但也被公认为优化领域中更为困难、更具挑战性的设计。通过拓扑优化，在给定材料品质和设计空间内，得到既满足约束条件又使目标函数最优的连续体布局形式，所产生的结果是全局最优解。

拓扑优化的最大优点是能在结构拓扑形状未定的情况下，根据已知边界条件和载荷条件确定比较合 理的结构形式，既能用于全新产品的概念设计，又能用于已有产品的改进设计。 文章将拓扑优化用于发动机支架的改进设计，取得了良好的设计效果。

2 拓扑优化的变密度法
2.1 拓扑优化变密度法的数学模型

结构拓扑优化的基本思路是将寻求结构的最优拓扑问题转化为在给定的设计区域内寻求最优材料分布的问题求解，对于连续结构拓扑优化，目前比较成熟的优化方法有：均匀法、变密度法、渐进结构优化法等。

文章采用变密度法进行发动机支架的拓扑优化，其基本思想是引入一种假想的密度值在[0，1]之间的密度可变材料，将连续结构体离散为有限元模型后，以每个单元的密度为设计变量 ，将结构的拓扑优化问题转化为单元材料的最优分布问题。
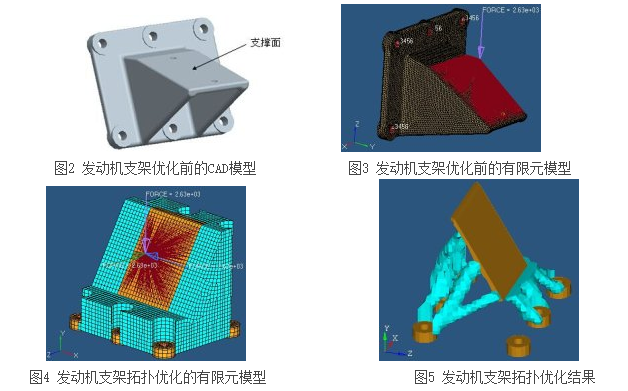
若以结构变形能最小为目标，考虑材料体积约束 (质量约束)和结构的平衡，则拓扑优化的数学模型为［2］：
  求 X = ( X1 ，X 2 ,…,X N ) T ,使得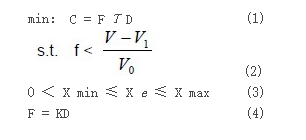
   

式中，C 为结构变形能；F 为载荷矢量；K 为刚度矩阵；D 为位移矢量；V 为结构充满材料的体积；V0 为结构设计域的体积；V1 为单元密度小于X max 的材料的体积 ；f 为剩余材料百分比；Xmin 为单元相对密度的下限；Xmax 为单元相对密度的上限。
在多工况的情况下，对各个子工况的变形能进行加权求和，目标函数变化为 ：

min： C = ∑W i C i            (5)

式中，W i 为第i 个子工况的加权系数，C i为第i 个子工况的变形能 。

2.2 拓扑优化的设计流程

HyperWorks 进行发动机支架的拓扑优化：首先在三维 CAD 软件Pro/E 中建立发动机支架的几何模型，通过STP 格式导入HyperMesh，在HyperMesh 中进行前处理，利用优化面板定义优化设计区域、目标函数和约束条件，最后在 OptiStruct 中进行拓扑优化迭代求解。

在HyperMesh 中，具体包括：有限元模型的设置(调用OptiStruct 模板及提取文件、设置材料和几何特性)；施加载荷和边界条件（创建载荷集合器、创建约束、施加载荷、创建载荷步）；设置拓扑优化参数（定义拓扑优化设计空间、定义优化的响应、定义目标函数和定义约束）；提交作业；查看结果。拓扑优化的设计流程如图1 所示。
用变密度法得到的拓扑优化结果是密度等值 面分布图 ,应力大的单元密度高，应力小的单元密度低 。事实上，材料密度可变在实际中是没法实现的，因此,在得到拓扑优化结果后要根据密度等值面分布图对结构进行人工处理以适应实际的工程需要［1］。

3 发动机支架的拓扑优化设计

3.1 发动机支架拓扑优化有限元模型的建立

如图2所示，发动机支架通过六个螺栓孔与车架纵梁相连接，其中的斜平面为支撑发动机的支撑面，发动机支架在车架左右两侧均布两个，共四个，支架材料为碳素铸钢ZG270-500，屈服极限为270MP，结合发动机的重量，每个支架上平均承载的压力大小约为2630N，支架的约束施加在与纵梁相连接的螺栓孔上，为了准确的反映结构受力和实际的约束情况，在螺栓孔周围将所有的节点通过刚性单元（RBE2）连接在一起，约束施加在刚性单元的主节点上，支架所承受的压力通过刚性单元（RBE2）施加在支撑面上，如图3所示，有限元模型的网格节点数为23529，网格单元数为95520，结合支架优化前的载荷和边界条件，进一步设计构想出支架拓扑优化的有限元模型，如图4所示，因为拓扑优化中是按照给定的材料体积百分比而不是按照应力大小的数值决定材料的取舍，因此，结构拓扑优化结果与载荷的大小无关 ，只与载荷的方向有关。

因此对其施加分别沿X,Y,Z负方向，大小为2630N的载荷集，在图4中，橙黄色为不变区域，深红色为刚性连接RBE2，其它为设计区域。在HyperMesh-OptiStruct提交计算可得拓扑优化的结果如图5所示。

3.2 建立发动机支架优化的CAD模型

根据图5拓扑优化的结果，结合具体的铸造工艺条件，进一步对发动机支架的原模型加以改进，即对其进行二次设计，得到支架优化后的CAD模型如图6所示。

3.3 发动机支架优化前后的有限元分析

  表1 发动机支架优化前后结果对比

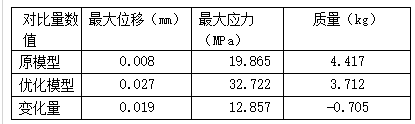
图7为优化后发动机支架的有限元模型，至图8至图11为发动机优化前后CAE分析结果对比，表1为其优化后的比较结果。
由以上的分析结果可以看出，改进之后的模型在相同的载荷作用下，最大位移和最大应力都较改进之前有所增大，但这是可以接受的，因为最大应力都远远小于材料的屈服极限270MP，但重量却减轻了0.705/4.417=15.96%，该支架生产批量极大，因此其拓扑优化结果将带来显著的经济效益。

5 结论

本文对发动机支架结构进行了基于有限元分析的拓扑优化设计。最终的优化支架，重量减小了 15.96％，由于在行驶中发动机支架不断受到来自路面的振动，今后应进一步考虑结构在不同路况和路面谱下的动态和疲劳分析，以提高结构的动态性能。
拓扑结构优化能够为工程设计人员提供结构概念性优化设计方法，将对传统设计形成挑战，缩短设计开发的周期，提高零件质量，从而增强企业的竞争力。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删