要点

• Hessian 矩阵是由多元函数的所有二阶导数组成的矩阵。
• 当计算 n 变量函数时，Hessian 矩阵是一个 n 阶对称方阵。
• 在优化问题中，计算 Hessian 矩阵以获得临界点，例如感兴趣的多变量函数的最大值/最小值。

数学建模广泛应用于工程和技术系统中，因为它使我们能够用数学术语描述现实生活中的问题。使用各种算法求解数学表达式和函数，并对解决方案进行优化以获得更好的结果。优化在基于数学模型解决工程问题中发挥着重要作用。获得的解决方案应满足约束条件并产生最大的输出和效率。

在优化过程中，大多数方法都会计算Hessian矩阵。Hessian 矩阵是达到以数学函数表示的系统全局最优值的一种方法。让我们探讨一下 Hessian 矩阵以及如何计算它。

什么是 Hessian 矩阵？

多变量函数在描述工程系统的数学模型中很常见。从多变量函数的二阶导数，可以了解函数的二阶行为。二阶导数在多变量函数中很重要，因为它们有助于确定优化中的关键点。

通常，计算Hessian 矩阵是为了了解依赖于多个值的函数的行为。Hessian 矩阵是由多元函数的所有二阶导数组成的矩阵。对于 n 个变量的函数，Hessian 矩阵是一个 nxn 方阵。由于微分的阶数不会带来导数的变化，因此Hessian矩阵服从对称性条件。当计算 n 变量函数时，Hessian 矩阵是一个 n 阶对称方阵。下面给出了广义 Hessian 矩阵 (Hf)。

Hessian 矩阵和标量值函数

函数将单个数字与每个点相关联的物理空间形成标量场。标量值函数可能采用多个输入值，但始终返回单个值。当标量函数依赖于多个值时，它形成多变量函数。Hessian 矩阵的计算仅对标量值函数有意义。在 Hessian 矩阵中，每个元素都是一个函数，并且在某个点计算相同的值，例如 (x ₀ .y ₀ ,...)。

_{对于点 (x 0} .y ₀ ,...)，前面提到的 Hessian 矩阵泛化可以重写为以下矩阵，假设标量场中存在 Hf (x ₀ .y ₀ ,...)：

如何计算 Hessian 矩阵

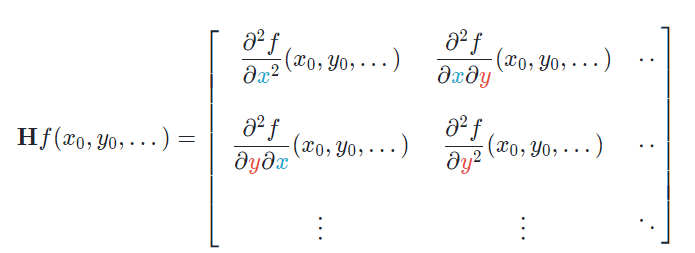
考虑一个可微函数 f：R ⁿ →R。该函数的 Hessian 矩阵可以按照下面给出的步骤计算。

1. 取函数 f 的梯度。设函数的梯度为 ▽f : R n →R

由一阶偏导数形成的矩阵称为雅可比矩阵或梯度矩阵。我们假设给定函数存在所有偏导数。

1. 取矩阵 ▽f 的梯度或导数。得到的结果是n阶方阵，构成f的Hessian矩阵。
2. 给定点(x 0 .y 0 ,...)处的Hessian矩阵可以通过代入Hessian矩阵的元素中的值来计算。

示例：计算 Hessian 矩阵

例如，我们计算 Hessian 矩阵：

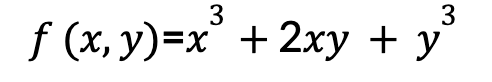
步骤 1：计算一阶偏导数。

步骤 2：计算二阶偏导数。

函数的 Hessian 矩阵为：

步骤 3：计算 (x,y)=(1,2) 处的 Hessian 矩阵

Hessian 矩阵对于优化至关重要

在优化问题中，我们计算 Hessian 矩阵以获得临界点，例如感兴趣的多变量函数的最大值/最小值。在工程中，Hessian 矩阵对于图像处理、计算机视觉和光谱中的频率计算等至关重要。大多数优化算法都会计算 Hessian 矩阵。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删