Hessian矩阵与优化之旅：凸性探索与CFD学习

要点

• Hessian 矩阵是一种处理二阶导数的数学结构。
• Hessian 矩阵始终是方阵，其维度等于函数变量的数量。
• 如果 Hessian 矩阵在集合 A 上的所有点都是半正定的，则该函数在集合 A 上是凸的。

有效解决工程问题需要优化，而工程中的大多数优化问题都是非凸的。为了解决非凸优化问题，使用 DC 函数。此类非凸问题的优化统称为DC优化，此类问题的理论称为DC规划。

DC 编程中使用的大多数算法都利用 Hessian 矩阵的优势及其凸性确定功能来迭代到更好的解决方案。在本文中，我们将讨论 Hessian 矩阵的基础知识，这对于使用计算算法优化解决问题非常重要。

海森矩阵

Hessian 矩阵广泛应用于工程问题的解决。它们用于优化代表系统的功能。Hessian 矩阵是一类处理二阶导数的数学结构。考虑一个由 n 个变量组成的函数 f。给出该函数的二阶偏导数的矩阵形成给定函数的 Hessian 矩阵。函数f的Hessian矩阵可以用下面的方程表示：

Hessian 矩阵的阶数

从上面给出的 Hessian 矩阵可以得出结论，它始终是一个方阵，其维度等于函数变量的数量。对于“n”变量函数，Hessian 矩阵的阶数为 n*n。

Hessian 矩阵的对称性

下面给出了 2 个变量的函数的 Hessian 矩阵。

在上面的 Hessian 矩阵中，您可以看到元素 fxy 重复两次，分别作为第一行第二个元素和第二行第一个元素。根据Schwarz定理或Clairaut定理，偏微分中微分的阶数并不重要，因此即使函数关于x和y以不同的阶数微分，元素也是相同的。

条件 Hij=Hji 适用于任意阶的所有 Hessian 矩阵，其中 i 和 j 分别表示行号和列号。每当方阵中的元素满足条件 Hij=Hji 时，它就形成对称矩阵。从目前的讨论可以得出，Hessian矩阵是满足对称条件的方阵。因此所有 Hessian 矩阵都是对称矩阵。

Hessian 矩阵与 Jacobian 矩阵

Hessian 矩阵由函数所依赖的所有变量对形成的二阶偏导数组成。雅可比矩阵也是基于函数偏微分的矩阵，但是是一阶偏导数。下面给出函数的雅可比矩阵。

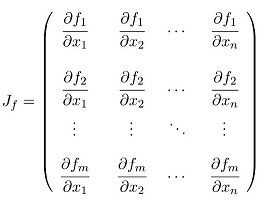
雅可比矩阵可用于确定函数的可逆性。当雅可比矩阵的行列式不为零时，可以对矩阵求逆。如果雅可比矩阵的行列式等于0，则函数可以求逆，也可以不求逆。

借助雅可比矩阵，可以计算多变量函数中的临界点。然而，要将临界点分类为最小值、最大值和鞍点，需要 Hessian 矩阵。让我们看看 Hessian 矩阵如何帮助找到最大值和最小值。

最小值、最大值和鞍点

雅可比矩阵给出函数的梯度。当函数 f 在某个点 x 的梯度为零时，该函数在 x 处具有临界点。为了确定临界点是局部最小值、最大值还是鞍点，可以利用 Hessian 矩阵。

如果 Hessian 矩阵是正定的，则临界点对应于函数的局部最小值。如果 Hessian 矩阵是负定的，则临界点对应于函数的局部最大值。

如果 Hessian 矩阵不定，则临界点对应于鞍点。类似地，Hessian 矩阵可用于识别函数的凸性和凹性。

使用 Hessian 矩阵确定函数的凸性

对于二阶导数连续的函数f，可以利用Hessian矩阵来确定其凸凹性。如果 Hessian 矩阵在集合 A 上的所有点都是半正定的，则该函数在集合 A 上是凸的。如果 Hessian 矩阵在集合 A 上的所有点都是正定的，则该函数是严格凸的。

一阶导数、Hessian 矩阵、凸性等知识对于采用基于梯度的算法获得工程问题的优化解决方案至关重要。在大多数计算软件中，采用基于梯度的算法来实现优化，例如顺序二次规划、有限内存 Broyden-Fletcher-Goldfarb-Shanno 方法、Levenberg-Marquardt 和 Gauss-Newton。

Cadence 的工具可以帮助您解决高度复杂的工程系统中的优化问题。订阅我们的时事通讯以获取最新的 CFD 更新或浏览 Cadence 的CFD 软件套件（包括Fidelity和Fidelity Pointwise），以了解有关 Cadence 如何为您提供解决方案的更多信息。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删