平板算例验证：固有频率与振型分析[Workbench版]

人们在制造动力机械、建造桥梁等工程实践中遇到大量灾害性振动问题，由此产生的噪声、疲劳等问题，吸引众多力学家和工程师致力于工程振动问题的研究，发展了近似分析方法、实验方法和有限元等方法。自从20世纪20年代起，振动逐渐成为机械工程师、结构工程师必须了解的知识，也是高等工程教育的重要内容之一。

本篇将采用ANSYS Workbench版，对此进行算例验证。

一、问题描述：

^{某一个矩形薄钢板，板的长度a=1 m，宽度b=1 m，厚度h=4 mm。材料密度ρ=7850 kg/m3，弹性模量E=200 GPa，泊松比μ=0.3。假设矩形薄板的四边铰支，计算该薄钢板的固有频率和振型。}

二、问题分析：

弹性薄板是指厚度比平面尺寸小很多的弹性体，它可提供抗弯刚度。在板中，与两表面等距离的平面成为中面。对板弯曲振动的分析基于下述Kirchhoff假设：

1）微振动时，板的挠度远小于厚度，从而中面挠曲线为中性面，中面内无应变。

2）垂直于平面的法线在板弯曲后仍为直线，且垂直于挠曲线后的中面；该假设等价于忽略横向剪切变形。

3）板弯曲变形时，板的厚度变化可忽略不计。

4）板的惯性主要由平动的质量提供，忽略由于弯曲而产生的转动惯量。

根据以上Kirchhoff假设，薄板固有频率的解析解为

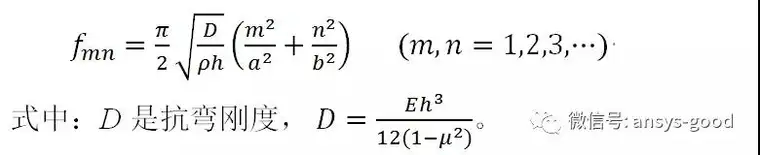
解析解参考文献：《机械振动基础》，胡海岩，pp118-121。

三、计算结果：

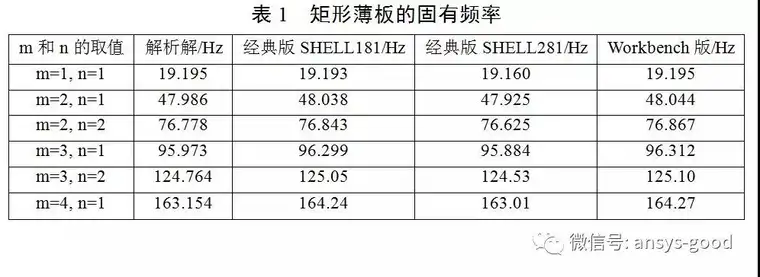
免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删