Ansys Workbench在管道疲劳强度分析及优化中的应用

0案例背景

管道从安装调试至投入使用期间，长期受到管道内部液体的循环作用力，会造成连接管道的螺栓发生疲劳破坏，造成管道漏液的危险情况。管道在输送液体时，连接管道的螺栓承受脉动循环载荷，主要受到了疲劳作用。通过实验的方法很难准确检测结构疲劳，因此工程上常用有限元计算来预估结构疲劳。有限元计算耗时少、效率高、节约成本，并且可以准确找到结构在受到循环载荷作用时的最薄弱位置。

具体做法是运用SolidWorks 建立几何模型，将几何模型导入ANSYS Workbench 中，先进行静力结构分析，包括两个计算环境，环境一为液体对管道的作用，环境二为螺栓预紧力对管道的作用。再将环境一的脉动循环载荷叠加在环境二的静载荷上，对管道结构进行非比例载荷疲劳寿命分析，并根据得到的疲劳寿命结果，优化螺栓预紧力大小，以实现管道疲劳寿命的最大化。

1 有限元分析

1.1 模型建立

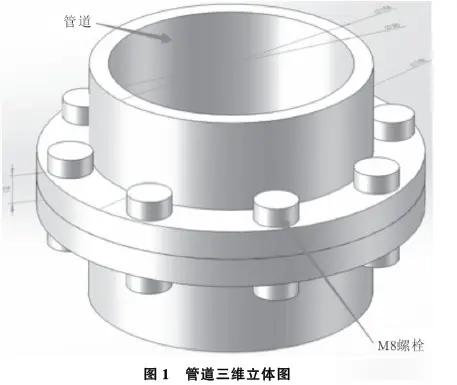
运用SolidWorks 建立如图１所示的管道，将几何模型保存成x_t格式，再将模型导入ANSYS Workbench 进行静力学计算。管道内径为90mm，外径为104mm，通过8个M8螺栓将管道连接起来。8个M8螺栓均匀分布在直径为122mm圆周上，管道法兰面厚度为12mm。

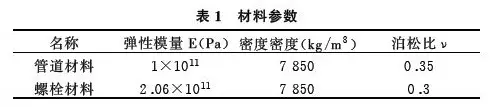
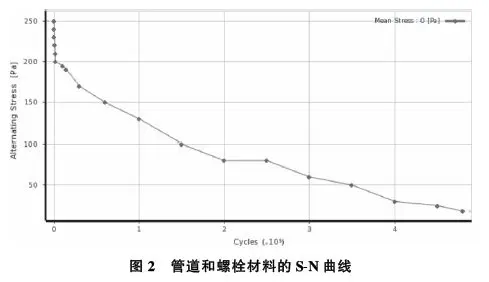
管道和螺栓的材料参数如表1所示，管道和螺栓的材料设计疲劳（S—N）曲线如图2所示。

选择8节点的3D 实体单元SOLID186 对管道及螺栓进行网格划分 ：

①对规则部分进行扫掠（Sweep）控制，网格尺寸（Element Size）大小设置为默认；

②对不规则部分进行六面体网格（HexDominant）划分，网格尺寸（Element Size）大小为：螺母部分设置为2mm ，管道法兰部分设置为4mm 。最终得到有限元模型总共具有节点82363个，单元30475个。

划分网格后的有限元模型如图3所示。

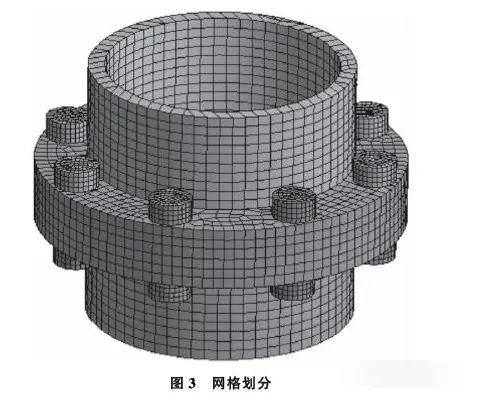
1.2 接触与边界条件

定义螺栓接触：在螺母与管道法兰接触的表面定义摩擦接触，将管道法兰表面定义成目标面，将螺母表面定义成接触面，摩擦系数设置为0.15，8个螺栓总计接触16处。在管道下半部分的内管壁上施加固定约束。

1.3 载荷边界条件

非比例载荷疲劳寿命分析管道受到螺栓预紧力和液体冲击力作用，其中螺栓预紧力大小恒定不变，而液体冲击力循环作用在管道上，使管道产生疲劳。由于液体对管道只会产生膨胀力，并不会产生收缩力，因此施加的应该是脉动循环作用力。

由于两种载荷的叠加作用，在进行有限元软件分析时需要采用非比例载荷疲劳寿命分析。该方法用两个加载环境取代单一的加载环境，进行疲劳寿命分析时不采用应力比，而是采用两个载荷环境的计算应力值来决定应力范围。计算时需要两个解，两组结果都会使用到，采用求解组合（Solution Combination）实现，基于两种环境的线性组合结果进行疲劳计算。

１）建立两个不同载荷的环境（Environment）。环境一：管道受到液体作用力，在管道上法兰施加压力3MPa，力的方向沿管道法兰表面法向向上；环境二：管道受到螺栓预紧力作用。螺栓预紧力由于是恒力，所以需要分成两个载荷步进行加载。在对应静力分析环境下，在分析设置（Analysis Settings）中设置载荷步的步数为2，接下来在螺栓螺纹的圆柱表面添加螺栓预紧载荷（Bolt Pretension），在Step1中设置预紧力大小，在Step2中定义锁定（Lock） 。

２）增加一个求解组合（Solution Combination）分支条，在工作表（Worksheet）中，添加用于计算的两个环境（Environments）。环境前的系数设置为1。

３）为求解组合（Solution Combination）添加Fatigue Tool，并将载荷类型定义为“非比例”（Non‐Proportional），疲劳强度因子设置为0.8。

４）定义疲劳寿命（Life），求解疲劳寿命大小。

1.4 恒定振幅疲劳分析

为了对比结果，首先对于环境一进行不考虑螺栓预紧力的静力计算，得到管道的最大von Mises应力值为121.85MPa，最大von Mises应力出现在螺栓根部。结果表明在受到液体作用力时，螺栓根部是最危险的位置，vonMises应力云图如图4所示，管道的整体变形云图如图5所示。

由变形云图可以看出，上法兰表面各个螺栓之间产生的变形较大，当管道受到载荷作用，管道的上下法兰面有分离趋势，有螺栓的部分由于受到螺栓限制，变形相对小一些。

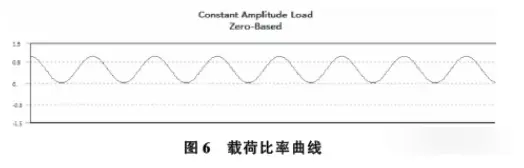
在环境一静力计算的基础上，添加Fatigue Tool模块，设置疲劳强度因子为0.8，由于管道在实际工作中只受到一个方向的作用力，载荷比率R设置为0，管道受到脉动循环载荷，载荷比率曲线如图6所示。

2 螺栓预紧力优化

ANSYS 本身具有进行优化分析计算的模块，Direct Optimization（Beta）（直接优化工具）、Goal Driven Optimization（多目标驱动优化工具）、Parameters Correlation（参数相关性优化分析工具）等。

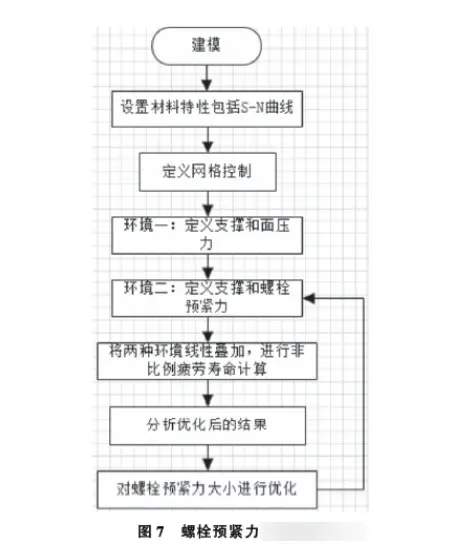
在这些工具中用户定义的设计变量主要是尺寸参数，目标函数是应力结果，而本文的设计变量是螺栓预紧力，目标函数为疲劳寿命，不能采用相应的优化分析模块进行计算。具体优化步骤流程如图7所示。

在ANSYS Workbench 有限元计算中，疲劳模块（Fatigue Tool）采用的原理是名义应力法。名义应力法是一种估算裂纹形成和裂纹扩展两部分总寿命的方法，是以名义应力为基本设计参数、以材料的S—N 曲线为主要设计依据的疲劳设计法，也称为影响系数或常规疲劳设计法。

疲劳破坏是一个累积损伤过程，不同研究者根据其对损伤累积方式的不同假设，提出了不同的疲劳累积损伤理论。其中被广泛认可的是Miner 线性累计损伤法则，该法则认为材料在各应力水平下的疲劳损伤是独立的，总损伤可以线性叠加，当总损伤达到某一数值时，构件则发生破坏。

Miner线性累计损伤法则的判别式如下：

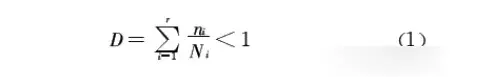
其中D为结构的损伤率，n为加载的循环周数，N为载荷对应的损伤周数（寿命）。例如，有S1和S2两种不同荷载，N1为荷载S1的损伤周数，N2为荷载S2的损伤周数。若先加n１周的荷载S1，损伤部分为n1/N1。再加n2周的荷载S2，对应的损伤部分为n2/N2，两个载荷的总损伤n1/N1＋n2/N2如果小于１，则认为结构不会产生疲劳损伤，满足抗疲劳要求，N1和N2可以由S—N 曲线求出。

压缩平均应力比零平均应力的疲劳寿命长，反之，拉伸平均应力比零平均应力的疲劳寿命短。当施加螺栓预紧力时，实际是使管道结构受到了压缩的力，提高了管道的疲劳寿命，当螺栓预紧力继续增大，管道最薄弱位置处的最大应力值会接近甚至超过材料的屈服强度值。

随着循环次数逐渐增加，管道的薄弱位置则会发生疲劳破坏，造成管道漏油，引起事故的产生。管道整体疲劳寿命云图如图8所示，管道主体部分包括管道法兰和管壁的疲劳寿命是无限寿命为4.8e５次（S—N曲线中材料定义的最大寿命），如图9所示，管道寿命最小的地方在螺栓根部。

由于管道液体对管道的作用力反复循环加载后，管道的疲劳破坏从应力最大的螺栓根部开始，疲劳寿命的计算结果也与静力分析时von Mises应力云图中螺栓根部应力最大的结果一致。

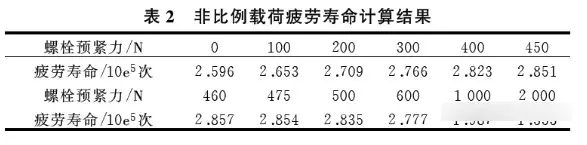
通过非比例载荷疲劳寿命分析，计算对应预紧力下的疲劳寿命结果，得到的数据如表2所示。

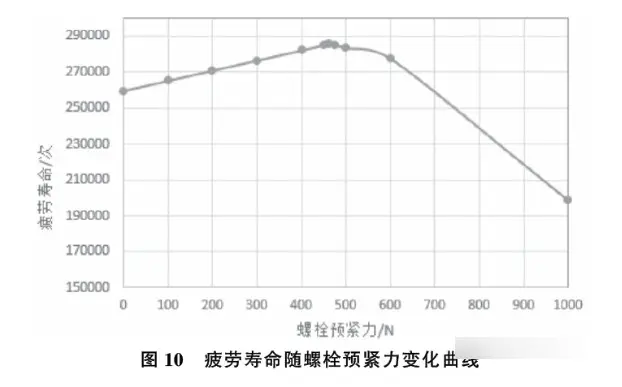
从数据中可以看出，当每个螺栓的预紧力从0N增大到460N的过程中，疲劳寿命一直在增加；当预紧力从500N继续增大时，管道的疲劳寿命逐渐减小。为了看清疲劳寿命随着螺栓预紧力增大的变化趋势，去除螺栓预紧力2000N的那组数据，根据表2得到的数据生成曲线图如图10所示。

当每个螺栓的预紧力达到460N左右，管道的疲劳寿命最大，可以达到2.857e5次。不施加螺栓预紧力时，管道的疲劳寿命为2.596e5次。因此，通过优化螺栓预紧力提高了管道10％的疲劳寿命。

3 结语

管道作为传输液体的组成部分，疲劳破坏会导致其出现结构损坏、漏液等危险事故。

本文利用SolidWorks软件建立了管道三维模型，然后导入ANSYS Workbench中得到有限元模型；利用ANSYS软件将管道分为液体作用环境和螺栓预紧作用环境两个环境对管道进行静力学分析，确定应力集中的位置；通过ANSYS Workbench的求解组合功能将两个环境的结果线性叠加，在此基础上计算非比例载荷疲劳寿命，求出在螺栓预紧力作用下的管道寿命长短；

再通过优化螺栓预紧力大小，使管道的疲劳寿命达到最大值，优化后的管道寿命在原有基础上提升了10%。研究结果为有效预估管道在非比例载荷作用下的疲劳寿命提供了基础，具有一定实用价值。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删