Ansys在钢箱梁焊接有限元模拟中的应用

钢箱梁是我国当今桥梁建设中的主要梁结构，在建与已建桥梁中有很大部分桥梁的上部结构采用钢箱梁。而钢箱梁一般是由工厂预制加工的，加工过程中必然会有钢板间的接缝需要进行焊接，使两块独立的钢板焊接成一个整体。在钢箱梁的钢板焊缝焊接过程中，移动的焊头会在瞬间产生高度集中的热量输入，热量的快速集中输入会导致钢板温度的骤升与骤降。钢属于一种温度敏感型的材料，受热升温时其体积会膨胀，降温时体积会收缩，体积的变化会导致结构内部应力分布的变化，钢箱梁结构的安全性也可能受到影响。所以若想了解钢箱梁焊接时的应力分布变化，保证钢箱梁结构的安全性与稳定性，有必要对焊接温度场的定量分析、预测、模拟。传统的焊接温度场和应力预测依赖于试验和统计基础上的经验曲线或经验公式，但是在航天、机械、土木等行业，焊接试验的成本巨大，当试验的工况较多或者试验失败时，会导致经济上的巨大损失。故本章运用大型商业有限元软件ANSYS经典界面进行数值模拟，在研究过程中利用了ANSYS内置的脚本语言APDL进行建模，分析钢板焊接过程的温度场。

1 钢板几何模型建立

为了简化钢箱梁的形状，节约数值模拟与实验的成本，本章将钢箱梁结构简化为一个长为0.2m、宽为0.15m、厚度为0.03m的块状几何模型，ANSYS中的几何模型效果如下图所示。

在上图的模型中，笔者标明了坐标系系统，在本章此后的位置信息的描述中，均采用此坐标系系统。

2 移动焊接热源的施加

在钢板焊接过程中，焊点热源作用在钢板上有一定面积，在该面积上的热量分布不是均匀的，中心点附近的热量较高，周围的热量较低。对于该种焊接热源的不均匀分布，现今很多学者将该热源的分布形式简化为高斯积分函数，本章参考前人的研究，采用高斯热源分布函数。

热源函数的三维函数图像如下图所示（假设_qm=1 J·s /m²，R=1m）。

移动焊接热源在钢板模型的上表面的中线位置施加，起始点的位置坐标为（0，0，0.03m）,并沿着y方向匀速移动至最终点（0，0.2m，0.03m）具体的施加位置、移动方向与移动轨迹如上图所示。如图所示，焊接中心点（0，0）位置处的热流密度最大，周围的热流密度随着与中心点的距离增大而减小。

据以上内容可知，在ANSYS中施加焊接移动热源需要明确的热源参数包括焊接电压U、焊接电流I、焊接热效率与电弧有效加热半径R。具体参数如表1所示。

表1 各温度下材料热属性参数

此外，在其他不试件移动热源的钢板表面，假设其与20℃的空气接触，此外，钢板的初试温度也设为20℃。

3 钢板材料的热属性参数设定

钢的热材料属性对温度较为敏感，在不同的温度下会呈现出不同的性质，在焊接过程中，钢板的温度变化较大，所以本文基于前人的研究成果及相关的规范确定了钢材在不同温度下的热材料属性^[1]。因参考资料的有限，本章中材料属性的最大温度设置到4000℃，当材料的温度大于4000℃时，ANSYS会自动根据4000℃以下的材料属性进行插值外推。

4 有限元网格的划分

本章中，单元类型设定为solid 70号单元。为了获得更加精确的结果，笔者将移动热源路径附近区域的网格进行细化，其网格尺寸为0.025m，将距离热源轨迹较远的位置的网格尺寸设置为0.05m，不同区域的网格均匀过度，具体划分效果如下图所示。

本章设定的焊接移动热源的移动速度为0.01m/s,钢板的长度为0.2m,所以热源在钢板上移动的时间为20s,笔者将求解时间设定为20s，求解的子步共设为50步，所以每一个子步的时长为0.4s。

5 单一速度下结果分析

分别提取0.4s、10s、20s时温度场分布云图如下图所示。

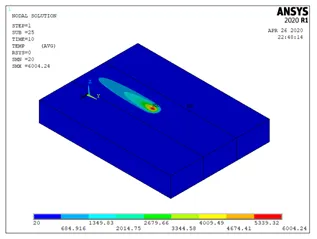
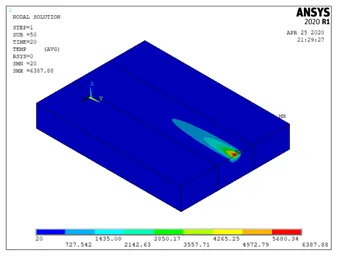
如图所示，热源荷载在随着时间的增加从轨迹的一端移动至轨迹的另一端。提取加载过程中，各子步模型的计算结果中的温度最大值，其变化曲线如下图所示。

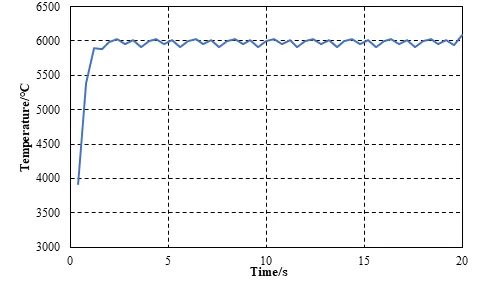
如上图所示，当热源刚加载在钢板上时，钢板模型的最大温度较低，为3922.67℃，到随着热源的移动，钢板的温度快速升高，在很短的时间内会达到一个稳定的范围，并在之后钢板模型的温度保持在较为恒定的范围，随着热源的移动会在6000℃左右有较小的波动。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删