某流媒体后视镜模态特性分析与优化设计

一、模态分析基础理论    

我们知道，实际的振动模型是有无限多个自由度的，而有限元分析技术就是用一个有限个自由度的模型去模拟无限自由度的模型。对于多自由度的振动系统，其动力学方程为

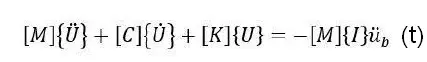
为了便于说明，现以单自由度系统为例，单自由度模型只有一阶模态，因此只有一个峰值，通过对动力学方程进行傅里叶变换和欧拉公式转换，得到频响函数FRF表达式

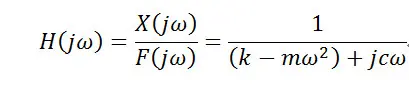
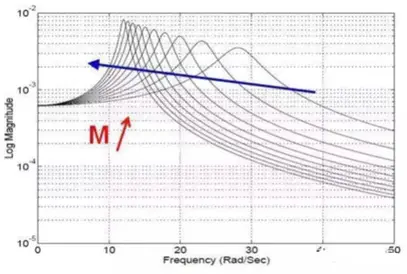
而由此公式得到的曲线图为

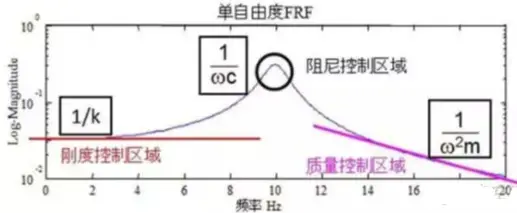
此图表明，共振频率点前的区域，由静刚度k控制，响应的大小由阻尼控制，共振频率点后的区域由动刚度ω²m决定，因此有如下结论：系统刚度k越大，共振频率越大；系统质量m越大，共振频率越小。

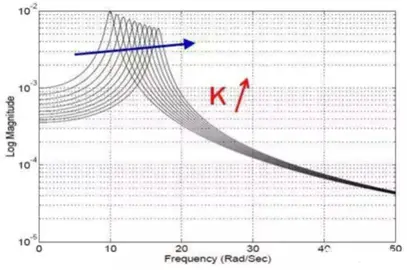
为了更直观的说明，则忽略单自由度系统的阻尼，根据(k-mω2)x=0存在非0解，有

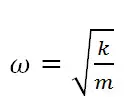
该等式表明，系统刚度k越大，共振频率越大；系统质量m越大，共振频率越小。

二、某案例分析

此案例为约束模态分析，采用Lanczos法和Abaqus求解器计算，模态截断阶数为30。

系统前三阶的模态分析结果为：

第一阶：

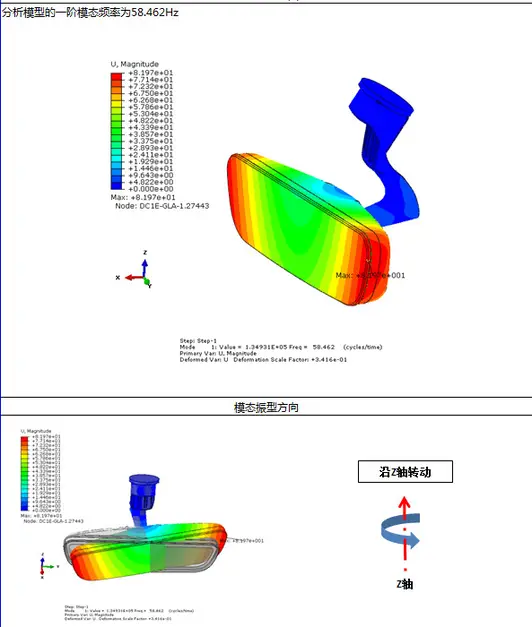
第二阶：

第三阶：

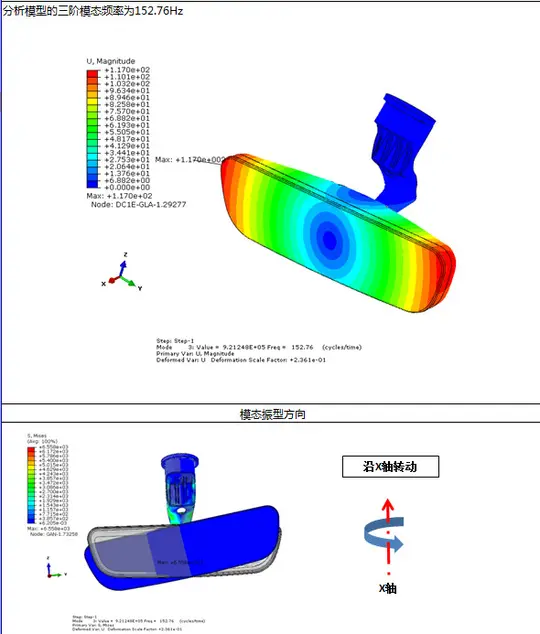
分析结果显示，第一阶的自然频率较低，需要进行结构优化，从而提高系统第一阶的自然频率。

前面理论部分阐述过，系统刚度k越大，共振频率越大；系统质量m越大，共振频率越小。而该系统本身的重量无法减小，所以只能通过改变刚度K，来增大共振频率。

根据振动系统的单元应变能结果显示（如下），颜色越接近红色的区域，应变能越大，应变能越大的区域，其刚度越小，所以通过单元应变能区，确定结构优化的重点区域和优化方式。

结构优化方式与优化结果：

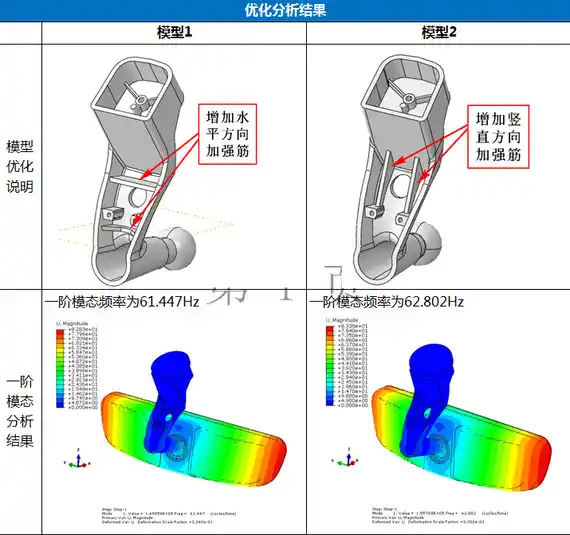
三、结论

1、结合模态分析理论，清楚模态的共振频率由哪些因素决定；

2、根据模态分析结果，明确系统模型的分析目的和优化方向（是增大还是减小模态频率来避开共振区，抑或直接降低频率响应幅值）；

3、通过模态分析结果的单元应变能变化区，确定结构优化的重点区域和优化方式。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删