1.背景及意义
盘为代表的管道连接结构常常是整个系统中最容易发生失效的位置,因此,对管道接头的接触分析就显得尤为必要,由于仿真能够观测处更准确的应力应变情况且时间及经济成本低,故本案例以法兰盘为例,对法兰盘管道接头进行仿真分析。
2.问题描述
图1给出了法兰盘的基本几何尺寸及法兰盘接头的物理模型,其中图1(A)为几何尺寸,图1(B)为物理模型。应当注意的是,考虑到连接处的局部效应,草图中保留了长0.1mm的管道(图中红色标志区域),也正因为如此,此法兰盘接头并非对称结果,但在仿真中,为节约分析时间对模型进行简化分析,采用轴对称单元进行分析,仿真分析全程采用统一的mm建模单位。
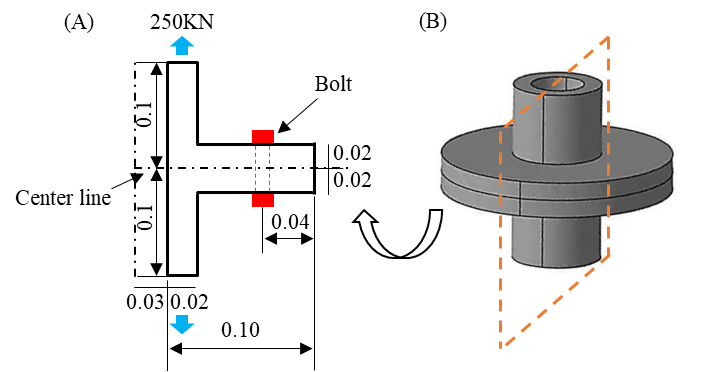
图1几何模型(A)几何尺寸(B)物理模型
3.有限元分析
模型采用外部导入方式打开,正式在Abaqus中分析的步骤如下图2所示。主要包括:查看法兰盘接头部件,检查部件模型信息是否丢失、查看部件属性(包括材料参数定义,截面塑性定义、单元定义)、查看装配、检查分析步设置、定义接触(采用自动面面接触)、定义约束(模型两端施加250KN)、最后定义初始边界条件(主要是温度场实现4次25摄氏度→350摄氏度的升温和350摄氏度→25摄氏度的降温)、之后对模型进行等向硬化分析,需要导入材料的实际塑性数据,应当注意:由于拉伸计的限制,一般拉伸样条测试得到的工程应力-工程应变曲线,需要转化为真实应力-应变曲线关系才能用于有限元分析材料的定义。真实的应力应变数据见附件,这里不再单独说明。
最后对导入的硬化数据表进行拟合,删除塑性数据中的最后一行重复数据即可提交求解。最后通过可视化后处理模块Visualization进行等效塑性应变及应力云图的分析查看·。
得到的云图结果如图3所示。可以发现,法兰盘接头的四周应变值较大,而中间靠近圆心的倒角处反而处于较低的应力应变范围。为了更加清晰反映最大等效塑性应变单元情况,提取出该单元的应力应变曲线如图4所示,其中图4(a)表示最大等效塑性应变单元的轴向应力应变曲线,图4(b)则表示循坏载荷下最大等效塑性应变单元的轴向应力应变曲线。进一步发现:第四次升温和第四次降温应力应变路径没有太大区别,没有表现加工硬化现象。
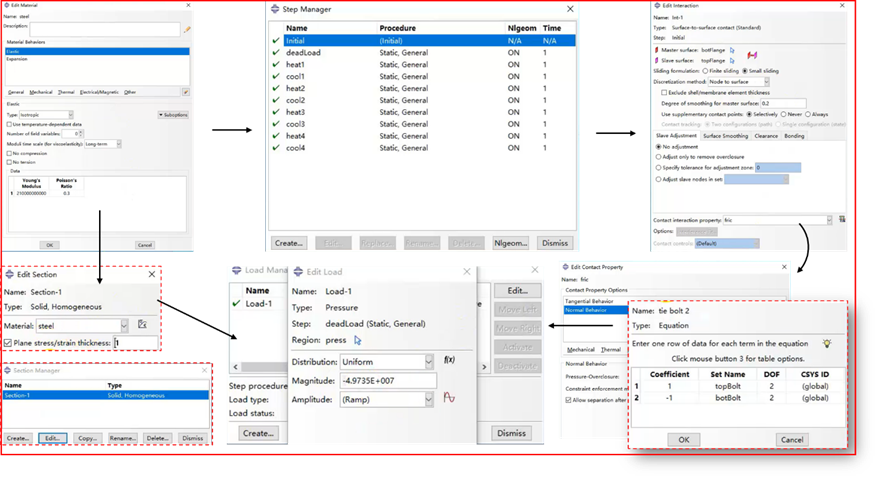
图2分析步骤
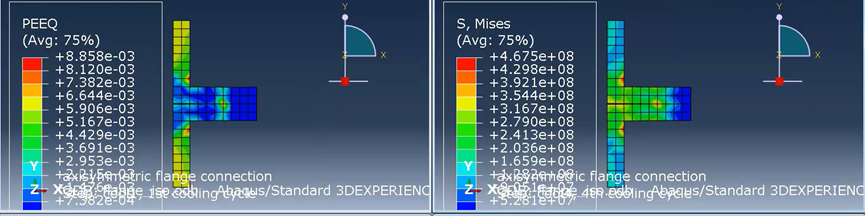
图3应力应变云图(PEEQ等效塑性应变、Mises应力)
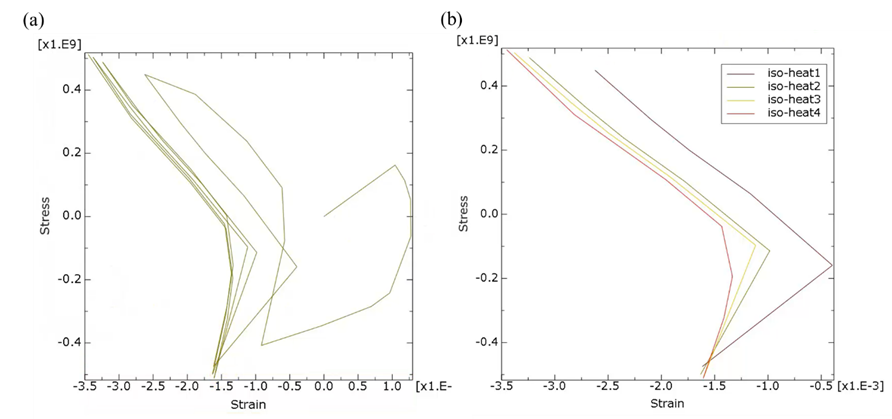
图4应力应变曲线(a)最大等效塑性应变单元的轴向应力应变曲线(b)循坏载荷下最大等效塑性应变单元的轴向应力应变曲线
4.结论
通过上述对法兰盘接头的接触仿真分析,基于等向加工硬化参数拟合方法并对比了结果差异,说明了该种仿真方法的一定合理性,可以为各种接头的接触分析提供思路,还可为复合材料RVE模型边界的设置提供参考。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删