Abaqus 3D打印建模新探索：极小曲面Python生成法

0.算例

下面是个简单的算例，在y方向压缩极小曲面之Gyroid，几何模型建立方法见下文，建立后阵列并有画网格导入abaqus即可。

【Abaqus 3D打印建模】之极小曲面 II --python生成极小曲面的图1

为了对比该极小曲面的应力水平，采用同样的材料做了单轴压缩，两种情况对比如图所示：

【Abaqus 3D打印建模】之极小曲面 II --python生成极小曲面的图2

从图中可以看到，如果仅去极小曲面上的一个点作为其应力应变，其曲线甚至比实心立方体还高，显然这是不合理的。出现这种现象的主要原因是，此类细观结构或变形不均匀时，不能取一个点代表整个模型，不然很可能会出现较大的误差。对此问题，细观力学有些方法，比如作用力反作用力法，体积平均法等，但也有人认为对于细观结构，作用力反作用力法不太合理。体积平均法的简单表达式如下：

【Abaqus 3D打印建模】之极小曲面 II --python生成极小曲面的图3

即模型中每一个单元的应力（应变）对单元体积积分后，除以模型整个体积。上述应力应变曲线也证实，采用该方法能够得到较为真实的数据。

那么，怎么通过体积平均法获得数据呢？在计算结束后，需要通过python脚本对数据进行处理，输出中需要EVOL（单元体积）以便获得各个单元的体积。

1.介绍

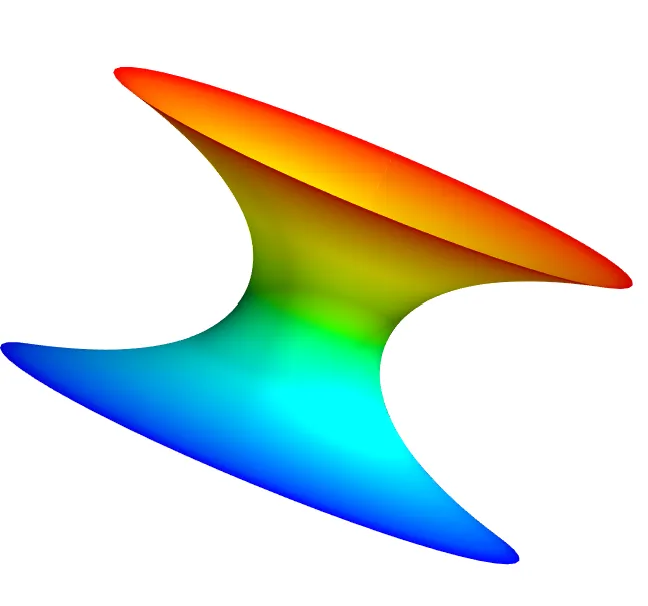
之前已经介绍过什么是极小曲面，同时根据表达式定义为 隐式和显式极小曲面，主要区别是隐式极小曲面一般只有一个方程，不容易将x,y,z独立表达出来，如下图所示：

今天介绍怎么用python生成上述极小曲面并输出为stl文件。

安装包：需要mayavi、vtk、traits及numpy等依赖包，可以从python第三方库下载，或者从https://pan.baidu.com/s/17Aa-Qv6YqvVLXjVqgW1b4A，（br5n）下载安装；
需要用到mayavi的mlab函数，实际上建模思路跟matlab完全一样，即先建立点阵区域，再从中获取满足极小曲面方程的点。
生成曲线的代码：

隐式曲线代码：

import numpy as np
from numpy import mgrid,pi,cos,sin,sinh,cosh
from mayavi import mlab
import mayavi
x, y, z =mgrid[-pi:pi:10j,-pi:pi:10j,-pi:pi:10j]v=cos(x)+cos(y)+cos(z)
iso=mlab.contour3d(x, y, z, v,contours=[0])
mlab.axes()
mlab.show()

显式曲线代码：

import numpy as np
from numpy import mgrid,pi,cos,sin,sinh,cosh
from mayavi import mlab
import mayavi,vtk
u,v=mgrid[-2*pi:2*pi:40j,-10:10:200j]
x=u*cos(v)
y=u*sin(v)
z=(2/3)*v
iso= mlab.mesh(x, y, z)
mlab.axes()
mlab.show()