ANSYS循环加载下的塑性累积问题探讨

金属有弹塑性行为，如果加载在弹性范围内，随卸载过程结构的几何变形会恢复至原样，这是因为弹性变形只是涉及到金属的延展性，并未涉及到原子间化学键的变化；而如果加载进入到塑性范围，则随卸载过程结构有一部分变形无法恢复，即塑性变形，塑性变形涉及到了金属原子间化学键的破坏和重组。因此金属进入塑性后，其应力应变曲线会发生改变。

很多人往往想要分析多次加载卸载（循环加载）情况下的塑性累积，这里面我们就需要考虑到塑性流动准则和硬化准则。

弹塑性本构模型    

弹塑性本构模型具有四个基本组成部分：屈服准则、塑性势函数、硬化规律和塑性流动法则。

• 屈服准则 是材料内某点达到塑性状态时应力分量间数量关系，用以定义初始屈服面和后继屈服面大小和形状。
• 塑性势函数 是表征塑性应变增量与加载面的关系，当前理论通常认为塑性势函数与屈服函数相近。
• 硬化规则 用来描述后继屈服面在应力空间中的演化规律。
• 流动法则 用来确定加载过程中塑性应变增量的方向。

案例  

在ANSYS软件中考虑塑性问题是，需要在材料属性中进行塑性定义，一般有Bilinear Isotropic Hardending和Bilinear Kinematic Hardening这两种塑性本构大类（以简单双线性为例）：等向硬化和随动硬化。其中，等向硬化不适于循环加载，随动硬化适合循环加载。我们以下面的模型为例对比两种材料本构的区别：

模型

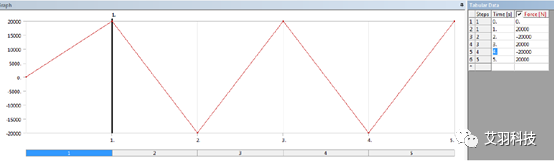
简单螺杆拉伸工况，一段固定，另一端循环加载（幅值20000N）

塑性定义：

分别定义两种塑性属性，通过在复 制后的项目中更换材料，实现单一参数（塑性定义）变化对比：

循环定义：

如下定义5个分析步。

结果

对比累积等效塑性应变：

等向硬化循环加载，屈服面增大一次，后继加载维持在屈服面内，没有更多塑性应变累积；

随动硬化循环加载，每一次循环，应力超过屈服面，屈服面移动一次，增加应力，塑性累积。

我们也可以绘制应力应变曲线来更形象的对比这两种材料定义所带来的区别：

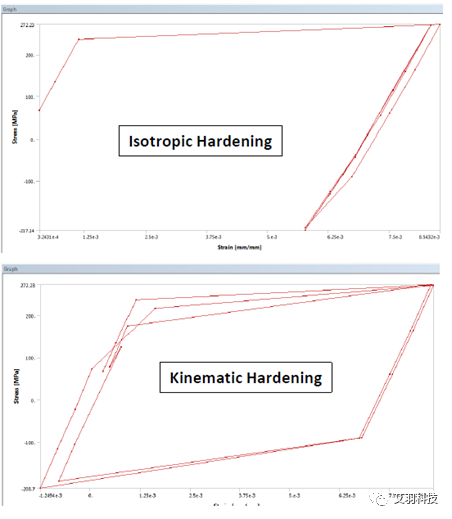
更详细的内容可以参考一些塑性理论或者高级非线性问题。如果对这个问题感兴趣的话，可以联系我们深入讨论。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删