ANSYS多点约束(MPC)的多案例展现其强大能力

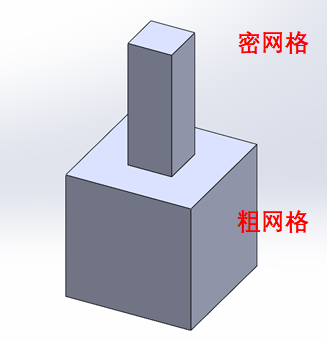
笔者在日常在做一些有限元分析的时候，经常会碰到由于面和面或者体和体之间的连接面不一致而导致不能用映射网格，若非要映射网格则需要大量的切分工作，但切分之后线和线的网格数量是要匹配的，因此对于网格疏密不同的连接地方很不好处理。比如对下图一个模型进行网格划分。(当然这里要求六面体网格）

MPC具体用法流程其实很简单，但其功能强大，至于使用流程仅简单介绍：（1）定义装配边界为接触单元和目标单元，设置单元的KEYOPT来指定采用MPC的接触算法，也是通过KEYOPT来指定具体的装配类型，最常见的就是绑定接触约束。

这里重点给出四个案例来详细说明一下MPC方法的使用和优点：

案例一：

在复杂的模型中，经常根据需要采用不同阶单元且网格疏密也不同，以便采用较小的求解花费而获得满意的结果。虽然将几何切分，采用不同的单元类型和网格尺寸来控制，也可以达到目的，但采用MPC方法 会更加方便。

如图网格疏密的划分，注意MPC装配边界重合但不共线，在边界处采用绑定的MPC约束。笔者将采用MPC方法的模型和仅用PLANE82单元划分的结果进行了对比，MPC方法的应力云图在装配边界上稍微不连续，但最大应力几乎无差别。

案例二：

网格疏密不同的变截面的悬臂梁，单元类型和网格疏密不同，计算结果与采用一种单元的结果几乎无差别。

案例三：

在曲壳上焊接平板，曲壳上下边固定，平板上施加均布载荷，平板处和曲壳处采用MPC连接。与全部采用SHELL181单元常规结果分析，位移结果误差很小，应力结果相差较大，但基本在5%内，这一是由于MPC方法在装配线处的应力结果误差本身较大，二是因为这种复杂曲壳结果本身就不能准确计算处应力值。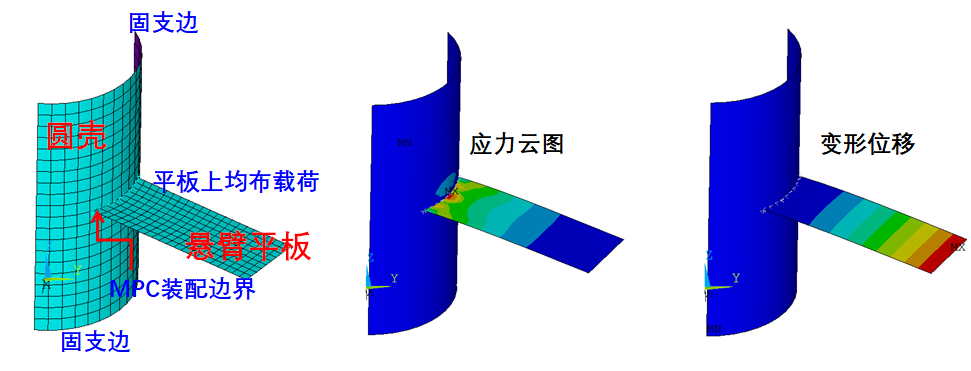

案例四：

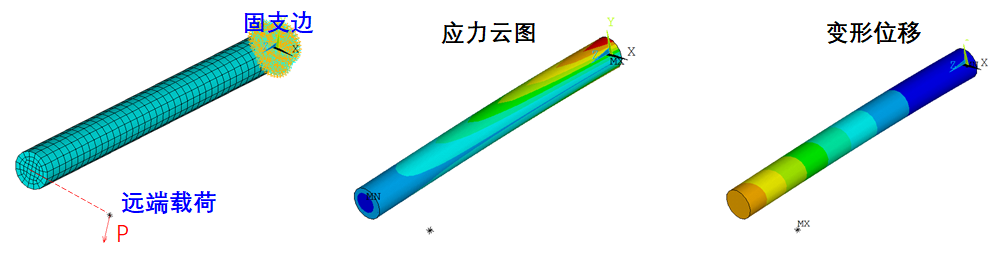
悬臂圆柱体的远距离加载，所谓的远距离加载，就是不在有限元模型上直接加载，而是通过与有限元模型很远的导向节点施加荷载，如下图示。

全文结束，感谢阅读。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删