FLUENT密闭空间氢气对流扩散模拟教程与实例分析

1 前言

之前我们做过不少有关氢气的案例，比如氢气泄漏模拟（可通过发送“氢气泄漏”查看），氢气爆炸模拟（可通过发送“氢气爆炸”查看），今天我们继续做一个常温常压的氢气对流扩散模拟，继续认识氢气的特性。

2 模型与网格

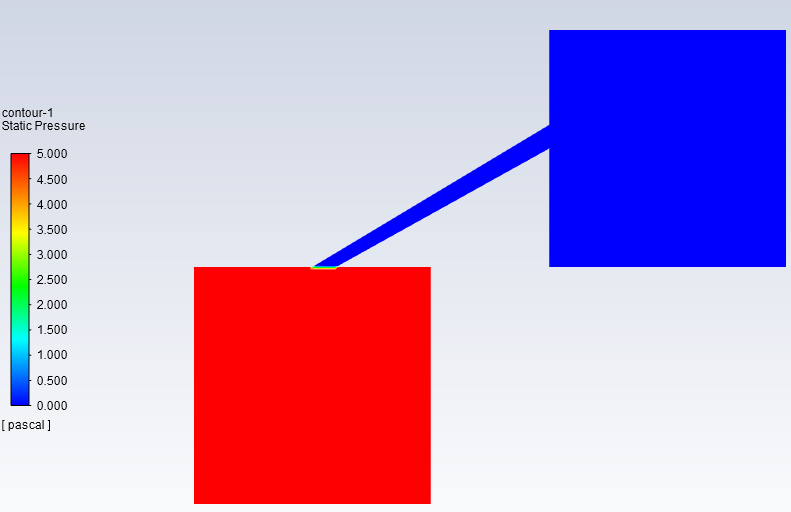
建立如下的二维平面模型，两个空间大小均为1000mm×1000mm，并通过一根管道相连。最开始下部空间充满体积分数18%的氢气空气混合物，初始压力5Pa，温度300K，所有壁面为绝热条件。

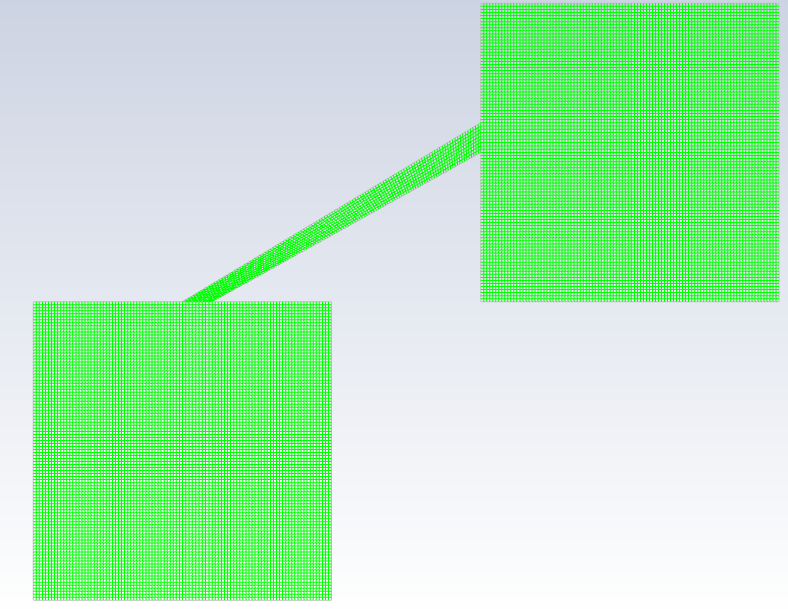
3 求解设置

启动能量方程和组分输运方程。

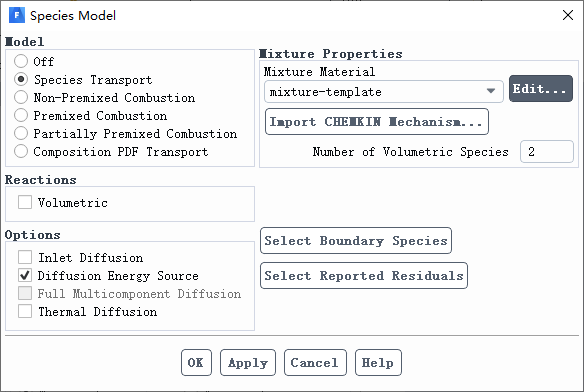
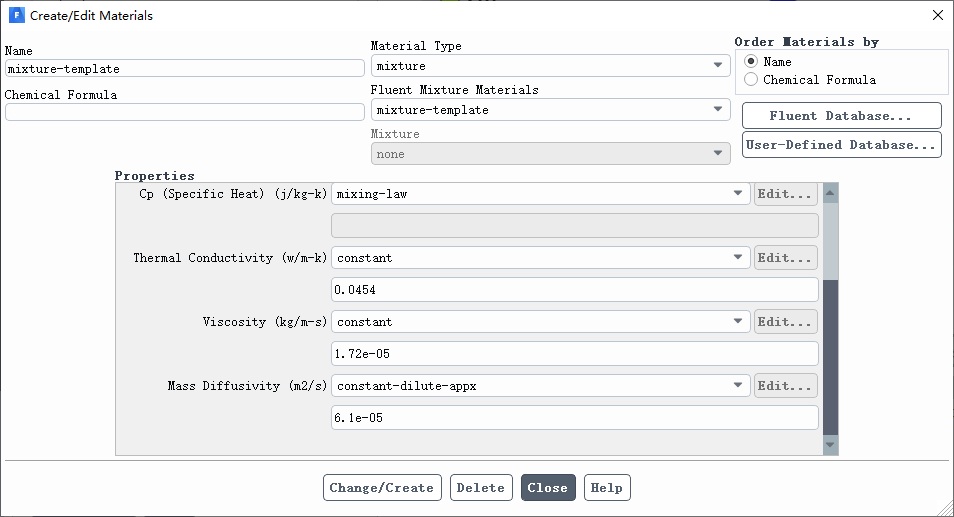
修改混合物组成为氢气和空气，其中空气置于最下面。

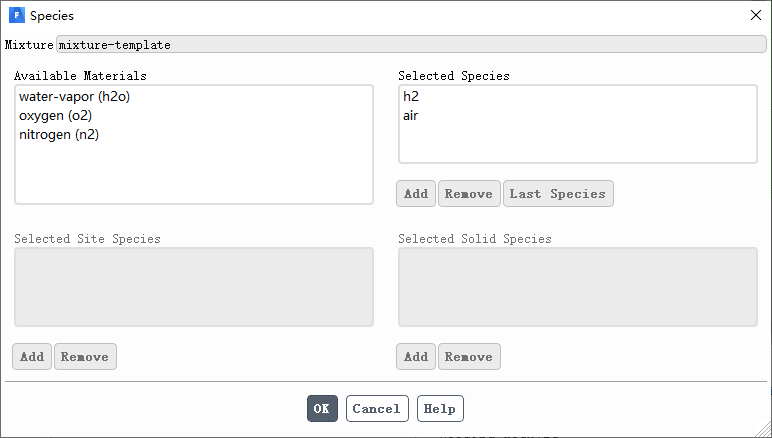
对于常温常压问题，可不考虑气体的可压缩性，混合物密度采用默认的不可压缩理想气体即可，则气体的密度由操作压力和域内温度根据理想气体状态方程求解。

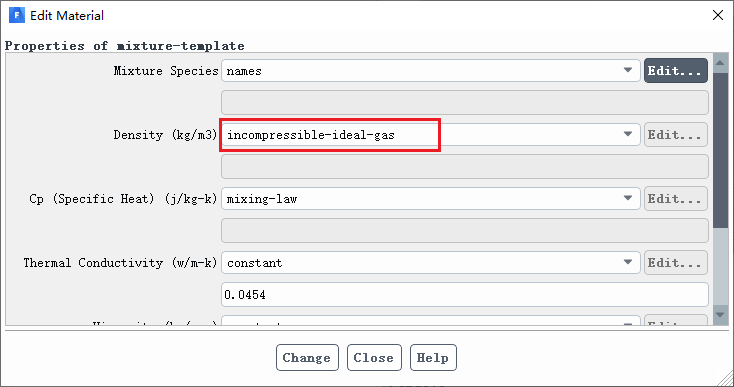
将扩散系数设置为6.1e-5。

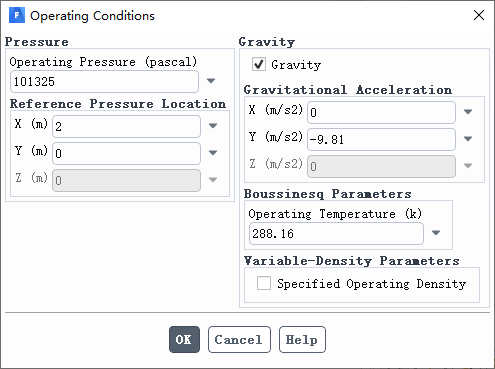
开启重力选项，并设置参考压力的位置，由于要初始化下部空间的压力，将参考压力位置设置到下部空间之外，这样就可以正确显示初始化后的空间压力。

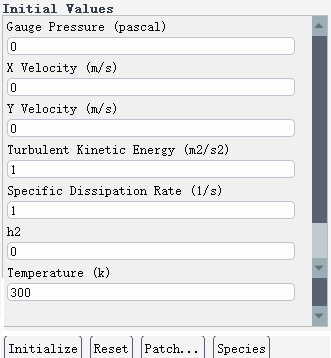
按下列初始条件进行初始化。

用patch功能将下部空间的氢气体积浓度和压力修改为18%（用质量分数0.01505进行patch）和5Pa。

设置两个监视器，分别监视上下空间中心的摩尔浓度（表征体积浓度）随时间变化规律。设置一个动画，用以动态显示氢气对流和扩散过程。

其他设置采用默认。采用瞬态求解（必须），时间步长设定为0.01s。

4 计算结果

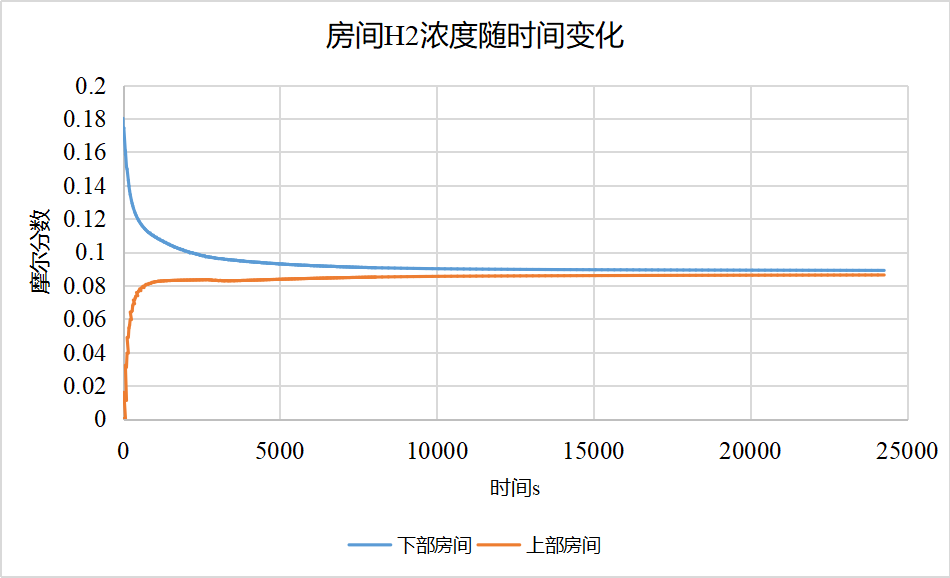
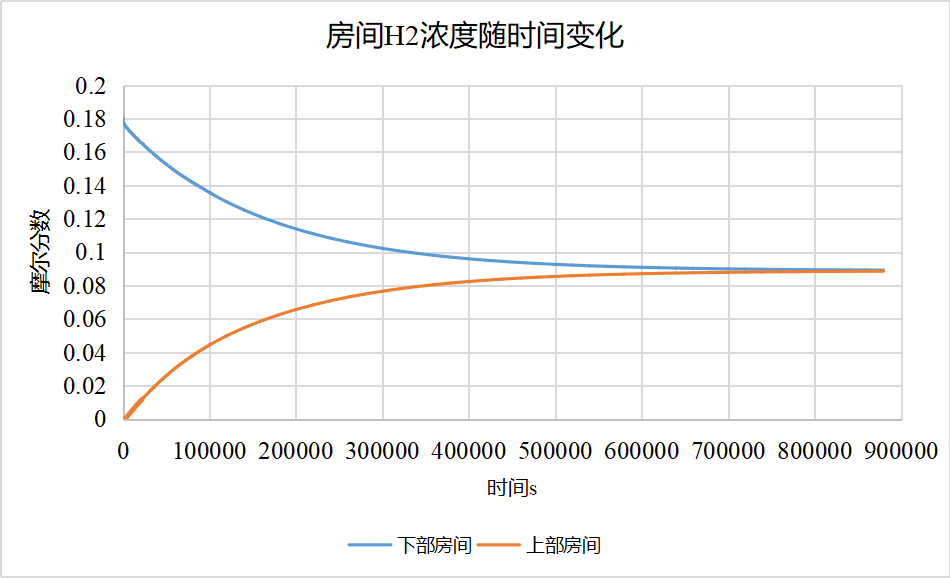
首先，上下两个空间中心的氢气摩尔浓度变化规律如下，可以看出开始阶段氢气的摩尔浓度变化迅速，之后趋于稳定，两个空间的摩尔浓度均趋近于0.09左右。这个很好理解，下部空间体积为1，整个计算域的体积为2.075，理论上充分混合后，空间内的浓度应该为0.18×1÷2.075=0.0867。

再看一下两个空间中心在垂直方向上的浓度分布，可以看出最终氢气浓度呈现上高下低的趋势，但是整体浓度值已相差不大，这是经历了相当长的时间后的结果，亦即氢气进行了充分的扩散和对流。

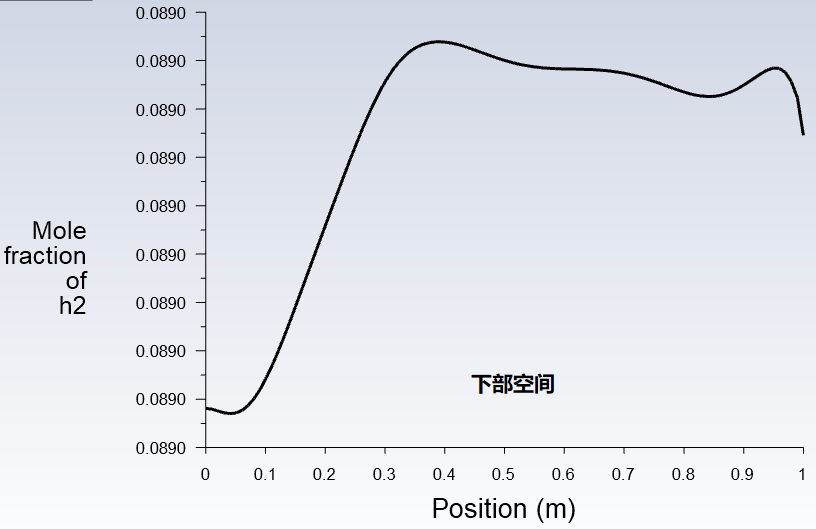
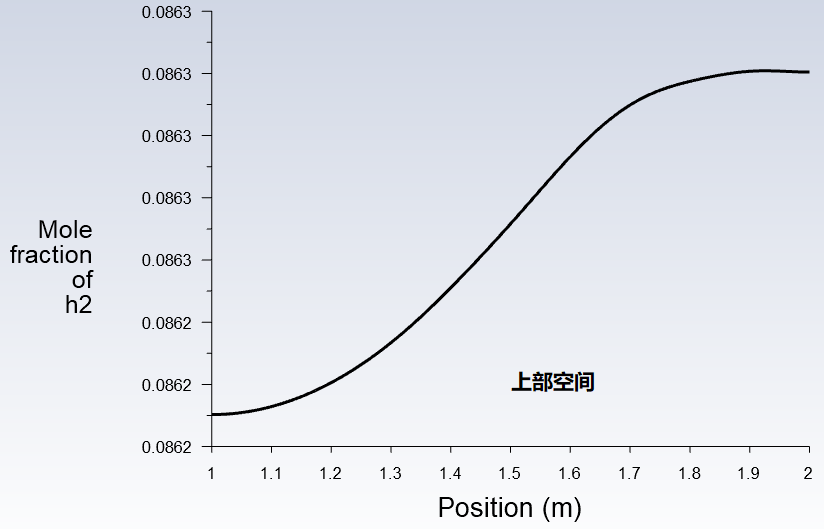
以上是综合考虑了对流扩散和浓度扩散过程，对流扩散是由于氢气和空气的密度差而产生，浓度扩散是由于氢气的浓度分布不均匀而产生。前者的效果是使得氢气浓度自上而下呈现高低分布，因为氢气密度很小而容易上浮。后者的效果是使得氢气浓度分布均匀，因为氢气由浓度高的地方扩散到浓度低的地方，当浓度分布均匀了也就没有扩散的驱动力。接下来我们不考虑对流扩散，仅仅考虑浓度扩散，关闭重力选项，关闭流动方程的求解。

只考虑浓度扩散时，上下两个空间中心的氢气摩尔浓度变化规律如下，可以看出浓度变化相对之前缓慢了许多，上下空间的浓度最终更好地趋于0.0867。

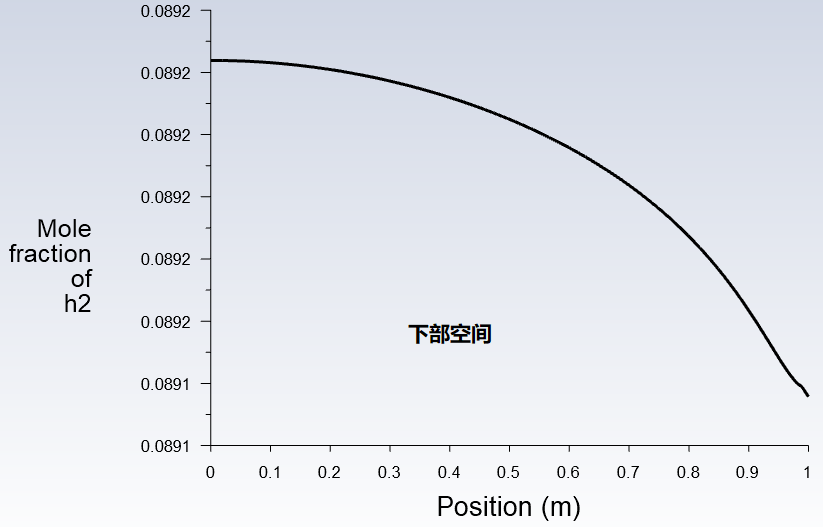
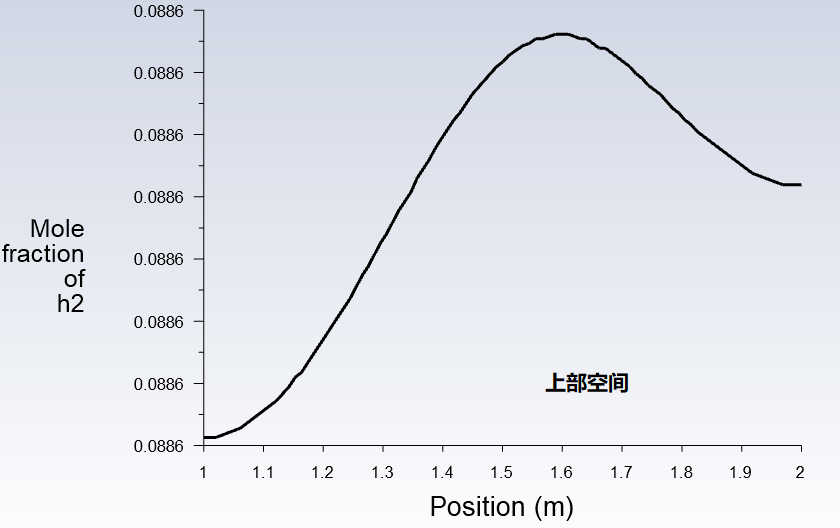
再看一下两个空间中心在垂直方向上的浓度分布，此时下部空间的浓度分布趋势与之前相反而呈现下高上低趋势，因为氢气是通过上部的管道扩散到另一个空间。下部空间的浓度分布同样呈现上高下低的趋势，因为氢气是从上部向下扩散的。

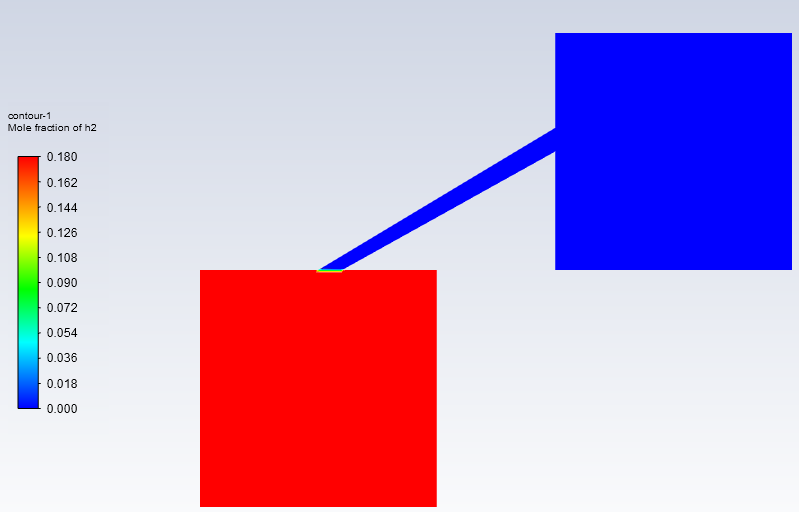
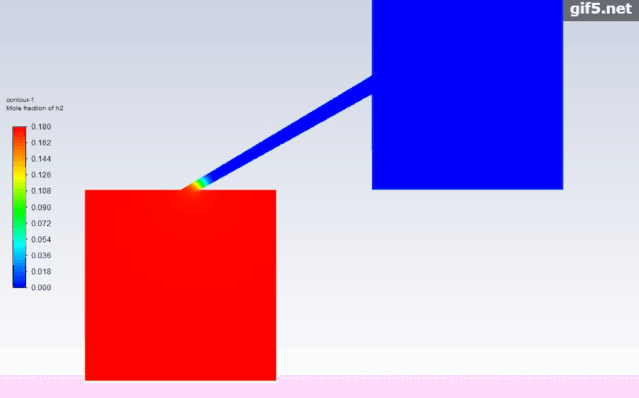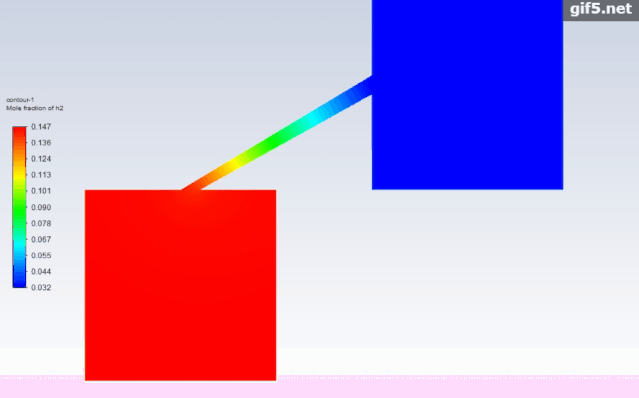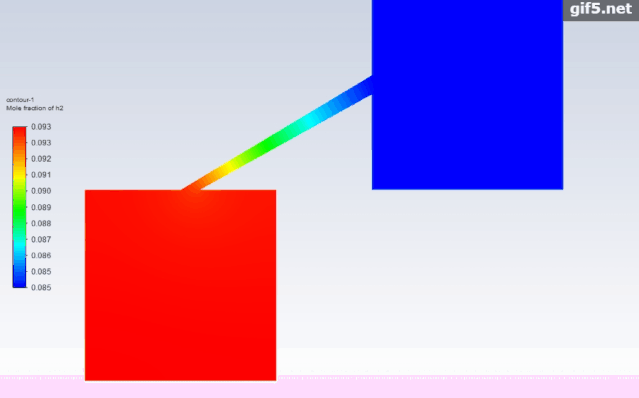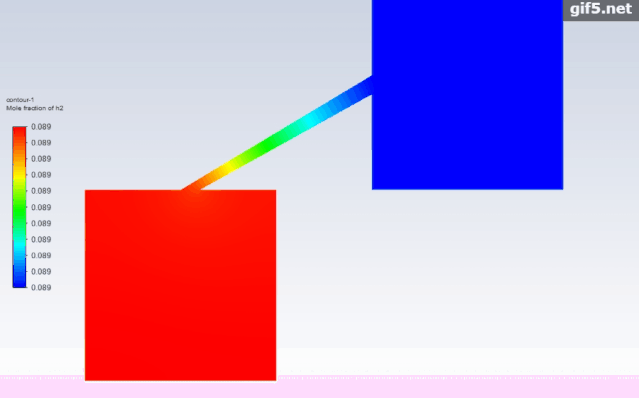
最后我们看一下两种情况下的氢气扩散过程动画，很显然综合考虑对流扩散和浓度扩散才更符合实际流动情况。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删