深入理解FLUENT中的接触热阻模拟方法

1 前言

两个名义上互相接触的固体表面，实际上接触仅仅发生在一些离散的面积元上，在未接触的界面之间的间隙常常充满了空气，热量将以导热的方式穿过这种气隙层，这种情况与固体表面完全接触相比，增加了附加的传递阻力，称为接触热阻。

接触热阻等于两个交界表面温度之差除以热流量。接触热阻单位是：㎡·K/W

FLUENT的计算模型中Solidification&Melting有现成的接触热阻模型，其他的计算模型没有发现，如果有就最好了，今天我们介绍一下用薄壁模型来模拟接触热阻的方法。

2 方法介绍

热流密度的计算公式为：

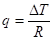
其中，R为接触热阻，单位㎡·K/W， q为通过两个固体之间的接触表面的热流密度，ΔT为接触面两侧的温度差。

我们知道，导热问题可以用傅里叶公式计算：

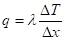
其中，λ为导热系数，单位W/m·K，Δx为热传导距离。

根据以上两个公式，可以推出接触热阻为：

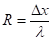
对应到FLUENT薄壁模型中，Δx为薄壁厚度，可以理解为接触热阻的等效厚度，λ为接触热阻的等效导热系数，这两个值都可以随意设定，只要保证两者相除等于接触热阻值即可。

3 问题描述

我们建立一个1m×1m的二维平面域，网格如下。计算域中间有一个薄壁，用来模拟接触热阻，上下两个计算域均为固体，材料为铝。上部三个边界均为20℃恒温壁面，下部三个边界均为80℃恒温壁面。接下来，我们求解接触热阻对传热量的影响情况。

4 计算结果

为了进行对比，首先，我们不考虑接触热阻，那么只要中间的薄壁厚度设置为0m，材料选择什么都无所谓了，如下图。

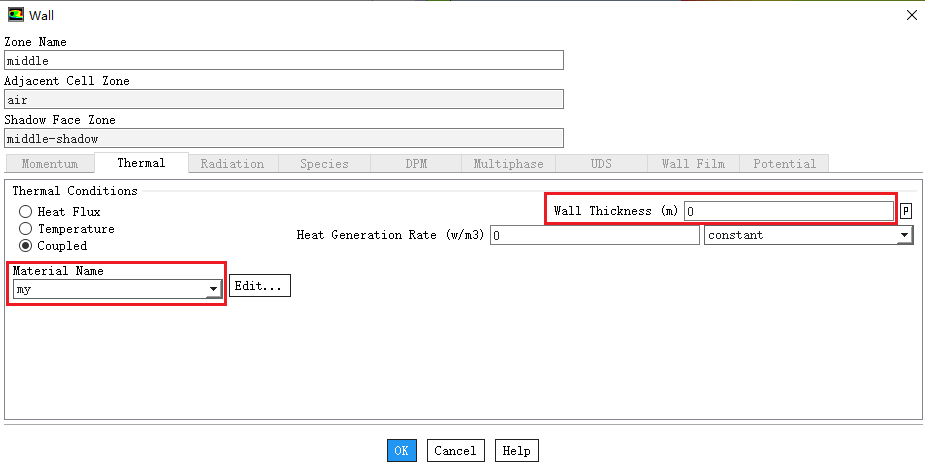
没有接触热阻时，通过上下壁面的传热量为46010W。

接下来，我们考虑接触热阻的影响。假设上下两块铝之间的接触热阻为0.0001㎡·K/W，如果我们将接触热阻等效厚度设置为0.001m，那么材料的等效导热系数应该为10W/m·K（材料通过自定义设置）。计算结果：通过上下壁面的传热量为36216W，相比于没有接触热阻的传热量小了不少。

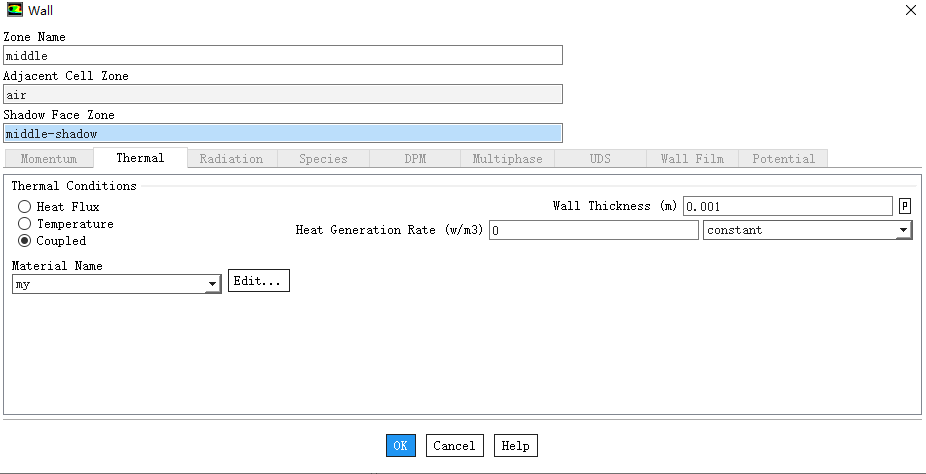
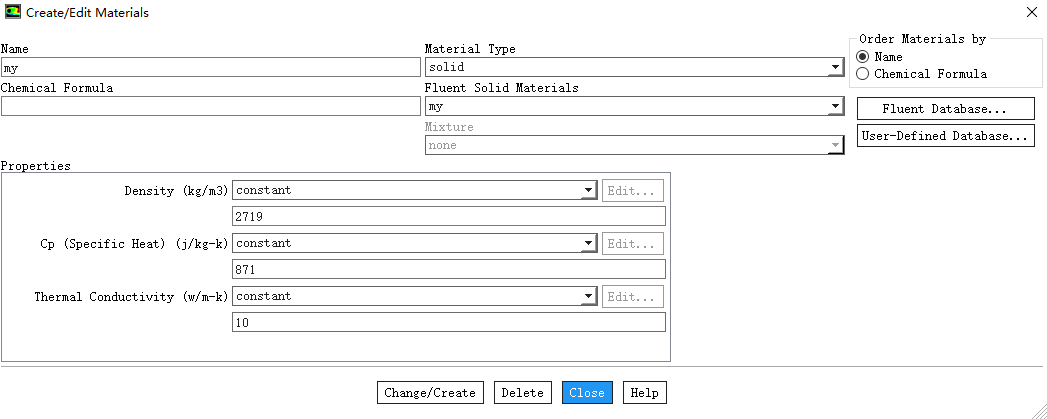
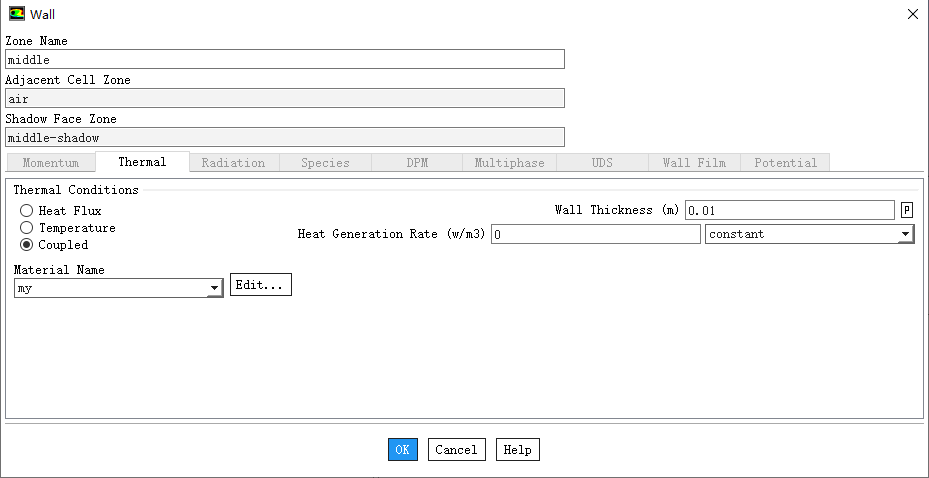
如果我们将接触热阻等效厚度为0.01m，那么材料的等效导热系数应该为100W/m·K（材料通过自定义设置）。计算结果：通过上下壁面的传热量同样为36216W，与前一种设置的计算结果完全一致。但是，还是建议大家在考虑接触热阻时参考一下相关标准，里面会有接触热阻大小和接触厚度的推荐值

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删