Fluent DPM模型UDF边界条件设置

在做颗粒流模拟时，常采用欧拉-拉格朗日方法，即采用欧拉方法对流场进行求解，采用朗格朗日方法对颗粒位置进行追踪。

但是，FLUENT的DPM模型中，都是基于球形颗粒的理想设定，例如

颗粒壁面条件。模型有粘附、反弹或给定反弹恢复系数。但实际应用时，若颗粒有确定的临界粘附速度，小于颗粒粘附，大于颗粒反弹，模型就没办法设置了。
曳力系数。模型给定的是球形颗粒的阻力系数，但是对于非球形颗粒，阻力系数往往偏大。如果想指定某一特定的阻力系数关联式，模型就没办法采用了。

虽然DPM模型设置中存在一些限制，但是FLUENT也为用户提供了自定义功能接口，这就是UDF。

一、UDF

1.1 什么是UDF

官方定义：UDF(User-defined function): C or C++ function that can be dynamically loaded with the ANSYS Fluent solver to enhance its standard features^[1].

意思就是，通过C或者C++函数，动态加载到fluent求解器中，增加一些功能。它有一些特点：

C或C++。需通过这两种语言编写。
DEFINE定义。通过采用宏定义加入求解器。
udf.h。需要udf.h头文件。
编译。需要编译且通过的编译后文件。

1.2 UDF的基本原理

UDF可以近似为一个函数，其基本运作即主函数输入参数，UDF返回参数。

[a, b, c] = func(a1, a2, a3, a4)

如上例，进入函数的参数为a1，a2,，a3和a4，返回的参数为a，b和c。因此只需要经营好函数中的具体算法就行了。

天下函数，万变不离其宗。

天下自定义子程序，皆万变不离其宗。

1.3 DMP模型的接口

常用的接口有如下

功能	宏	添加位置
边界（Boundary）	DEFINE_DPM_BC	Boundary condition
体积力（Body）	DEFINE_DPM_BODY_FORCE	Discrete Phase Model
曳力（Drag）	DEFINE_DPM_DRAG	Discrete Phase Model
侵蚀（Erosion）	DEFINE_DPM_EROSION	Discrete Phase Model
初始注入（Injection）	DEFINE_DPM_INJECTION_INIT	Set Injection Properties
采样（Sampling output）	DEFINE_DPM_OUTPUT	Sample Trajectories
物性（Properties）	DEFINE_DPM_PROPERTY	Create/Edit Materials
...	...	...

比较常用的有边界、曳力、侵蚀、采样等等。

接下来选几个具体讲一讲。

二、边界 DEFINE_DPM_BC

2.1 用法

DEFINE_DPM_BC(name, tp, t, f, f_normal, dim)

进入udf参数

类型	参数	解释
symbol	name	UDF的名字
Tracked_Particle	*tp	被追踪颗粒的数据集
Thread	t	我也没懂，好在没用到
face_t	f	颗粒撞击的面的index
real	f_normal	垂直面的单位向量
int	dim	维度，2D为2，3D为3

类型比较好理解，tp是颗粒的数据集，结构体形式，包含颗粒的所有信息，如下

TP_POS(tp)[i] /*position*/
TP_VEL(tp)[i] /*velocity*/
TP_DIAM(tp) /*diameter*/
TP_T(tp) /*temperature*/
TP_RHO(tp) /*desity*/
TP_MASS(tp) /*mass*/
TP_TIME(tp) /*time*/
TP_DT(tp) /*time step*/
TP_FLOW_RATE(tp) /*flow rate*/
TP_LMF(tp) /*liquid mass fraction*/ 
......

f_normal非常重要，经过研究，我认为此单位向量是由颗粒指向壁面，如下图。

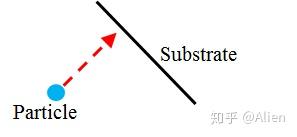
dim好理解，即维度，2D为2，3D为3。注意，2D旋转对称模型虽然是二维，但本质是3D。

返回参数

采用return返回参数，有以下类型

颗粒状态

return PATH_ACTIVE /* Continue to track */
return PATH_ABORT /* Stopped and Aborted */
return PATH_END /* Stopped but escaped */

PATH_ACTIVE 继续追踪

PATH_ABORT 终止，一般是因为错误而终止

PATH_END 停止，和abort是有本质区别的，是程序逻辑上的终止

2. 颗粒参数

TP_VEL0[dim]

直接对颗粒速度进行赋值。例如

for(i=0; i<dim; i++)
      TP_VEL0[i] = 1.;

返回后，下次计算时颗粒的初始速度就被更改了。

2.2 示例

FLUENT的帮助文档给了一个示例，因此我想通过示例，来解释该怎么用。

以下经过拆分，方便讲解，连在一起就是完整程序。

1. 初始定义

/* reflect boundary condition for inert particles */
#include "udf.h"
DEFINE_DPM_BC(bc_reflect,tp,t,f,f_normal,dim)
{
	real alpha; /* angle of particle path with face normal */
	real vn=0.;
	real nor_coeff = 1.;
	real tan_coeff = 0.3;
	real normal[3];
	int i, idim = dim;
	real NV_VEC(x);

例如，这里udf的名字为bc_reflect，定义了一些参数，如

alpha，颗粒与壁面之间的夹角
vn，法向速度
nor_coeff，法向恢复系数
tan_coeff，切向恢复系数
normal，法向向量

2. 判断类型

#if RP_2D
/* dim is always 2 in 2D compilation. Need special treatment for 2d axisymmetric and swirl flows */
if (rp_axi_swirl)
{
	real R = sqrt(TP_POS(tp)[1] * TP_POS(tp)[1] +
	TP_POS(tp)[2] * TP_POS(tp)[2]);
	if (R > 1.e-20)
	{
		idim = 3;
		normal[0] = f_normal[0];
		normal[1] = (f_normal[1] * TP_POS(tp)[1]) / R;
		normal[2] = (f_normal[1] * TP_POS(tp)[2]) / R;
	}
	else
	{
		for (i = 0; i<idim; i++)
			normal[i] = f_normal[i];
	}
}
else
#endif

此功能是求解法向向量。这是因为，2d旋转对称的向量是二维，但是实际其实是三维，因此需要特殊求解法向向量。

3. 具体模型

for (i = 0; i<idim; i++)
	normal[i] = f_normal[i];
	if (TP_TYPE(tp) == DPM_TYPE_INERT)
	{
		alpha = M_PI / 2. - acos(MAX(-1., MIN(1., NV_DOT(normal, TP_VEL(tp)) / MAX(NV_MAG(TP_VEL(tp)), DPM_SMALL))));
		if ((NNULLP(t)) && (THREAD_TYPE(t) == THREAD_F_WALL))
			F_CENTROID(x, f, t);
/* calculate the normal component, rescale its magnitude by the coefficient of restitution and subtract the change */
	for (i = 0; i<idim; i++) 
		vn += TP_VEL(tp)[i] * normal[i]; /* Compute normal velocity. */
	for (i = 0; i<idim; i++)
		TP_VEL(tp)[i] -= vn*normal[i]; /* Subtract off normal velocity. */
	for (i = 0; i<idim; i++)
		TP_VEL(tp)[i] *= tan_coeff; /* Apply tangential coefficient of restitution. */
	for (i = 0; i<idim; i++)
		TP_VEL(tp)[i] -= nor_coeff*vn*normal[i]; /* Add reflected normal velocity. */
	for (i = 0; i<idim; i++)
		TP_VEL0(tp)[i] = TP_VEL(tp)[i]; /* Store new velocity in TP_VEL0 of particle */
	return PATH_ACTIVE;
}
return PATH_ABORT;
}

第一步，不是2d旋转对称的话，f_normal就是法相向量。

第二步，求解夹角

第三步，开始修改颗粒参数啦

Compute normal velocity

/* Compute normal velocity. */
for (i = 0; i<idim; i++) 
      vn += TP_VEL(tp)[i] * normal[i];

求解法向速度，思路是

TP_VEL(tp)[0]* normal[0] + TP_VEL(tp)[1]* normal[1] + TP_VEL(tp)[2]* normal[2]

就是法向速度，因为normal是法向向量。

而且，normal是颗粒朝向平面的，所以vn一定是个非负值。

Subtract off normal velocity

/* Subtract off normal velocity. */
for (i = 0; i<idim; i++)
      TP_VEL(tp)[i] -= vn*normal[i];

是从速度TP_VEL中移除法向速度，所以是求解切向速度，思路是

vn*normal[0] + vn*normal[1] + vn*normal[2]

是速度的法向分量，那么

(TP_VEL(tp)[0] - vn*normal[0]) + (TP_VEL(tp)[1] - vn*normal[1])  + (TP_VEL(tp)[2] - vn*normal[2])

就是切向速度了。重新赋值以后，TP_VEL(tp)就只有切向分量了。

FLUENT一行代码就写清楚了，佩服佩服。

Apply tangential coefficient of restitution

/* Apply tangential coefficient of restitution. */
for (i = 0; i<idim; i++)
      TP_VEL(tp)[i] *= tan_coeff;

施加切向恢复系数，思路是

TP_VEL(tp)是切向分量，那么TP_VEL(tp)*tan_coeff就是对切向分量施加恢复系数。

Add reflected normal velocity

/* Add reflected normal velocity. */
for (i = 0; i<idim; i++)
      TP_VEL(tp)[i] -= nor_coeff*vn*normal[i];

这里再切向分量基础上，又把法向加回去，且施加了法向恢复系数，思路是

nor_coeff*vn*normal[0] + nor_coeff*vn*normal[1] + nor_coeff*vn*normal[2]

是法向分量，但是因为颗粒碰壁以后，速度大小不变，方向相反，所以

-nor_coeff*vn*normal[0] - nor_coeff*vn*normal[1] - nor_coeff*vn*normal[2]

是颗粒反弹速度的法向分量。切向速度大小方向不变，所以

(-nor_coeff*vn*normal[0] + TP_VEL(tp)[0]) +
(-nor_coeff*vn*normal[1] + TP_VEL(tp)[1]) + 
(-nor_coeff*vn*normal[2] + TP_VEL(tp)[2])

就是颗粒反弹后的速度了。fluent代码一行，佩服佩服。

然后修改颗粒速度啦。

Store new velocity in TP_VEL0 of particle

/* Store new velocity in TP_VEL0 of particle */
for (i = 0; i<idim; i++)
      TP_VEL0(tp)[i] = TP_VEL(tp)[i];

这个比较简单。

然后让颗粒继续追踪，所以返回

return PATH_ACTIVE

如果颗粒碰壁就粘附，那就不继续算了，返回

return END

注意，是END不是ABORT。

4. 如何加入UDF

UDF编写并编译成功后，在边界条件处加入UDF。

如下图，在wall选项中，DPM子选项中选择自定义函数即可。

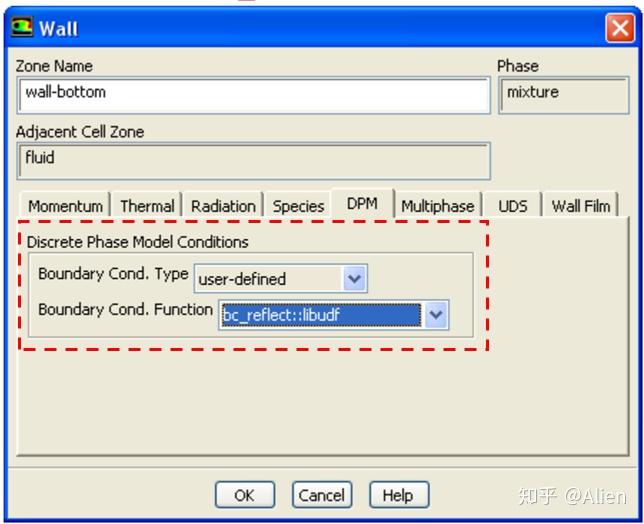
5. 总结

这样一来，DEFINE_DPM_BC的具体功能很好理解。

如果想实现更多功能，在此基础上修改就好了，例如施加临界粘附速度。

假如临界粘附速度是vc，那么vc<vn时，颗粒粘附，vc>=vn时，颗粒反弹，程序即为

for (i = 0; i<idim; i++) 
      vn += TP_VEL(tp)[i] * normal[i]; /* Compute normal velocity. */
if(vn<vc)
{
      return PATH_END;
}
else
{
for (i = 0; i<idim; i++)
      TP_VEL(tp)[i] -= vn*normal[i]; /* Subtract off normal velocity. */
for (i = 0; i<idim; i++)
      TP_VEL(tp)[i] *= tan_coeff; /* Apply tangential coefficient of restitution. */
for (i = 0; i<idim; i++)
      TP_VEL(tp)[i] -= nor_coeff*vn*normal[i]; /* Add reflected normal velocity. */
for (i = 0; i<idim; i++)
      TP_VEL0(tp)[i] = TP_VEL(tp)[i]; /* Store new velocity in TP_VEL0 of particle */
return PATH_ACTIVE;
}

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删

返回上级列表

请

联系我们

，获取更多内容

< 上一篇: Fluent瞬时模拟结果时均化方法

下一篇: Fluent离心泵旋转流场模拟实战 >