ANSYS WORKBENCH热电耦合应用实例浅析

1 前言

      电流流经导体时会产生热量，叫做焦耳热，使得导体温度上升，焦耳热计算公式为Q=I²R（W）。

电气设备、部件经常要考虑导电温升情况，今天我们用ANSYS WORKBENCH做一个简单的热电耦合案例。

2 模型建立

      建立如下的导体模型，两段导体的长度均为50mm，截面分别为5mm×5mm和2mm×2mm。

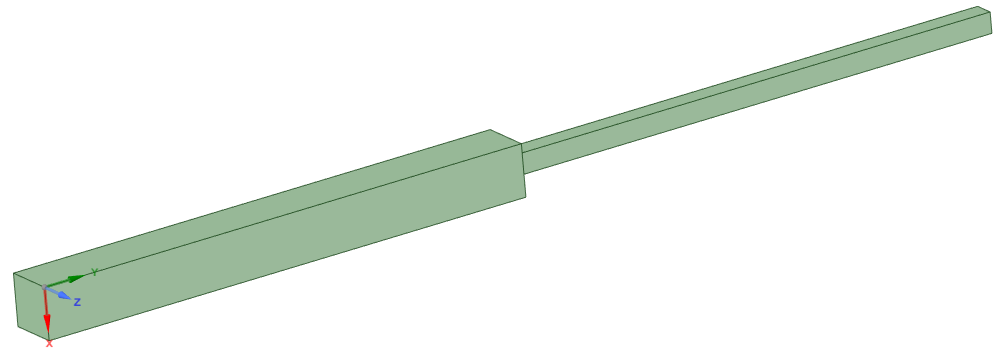
      导体的材料属性如下。

3 计算设置

      在WORKBENCH建立热电模型，如下图。

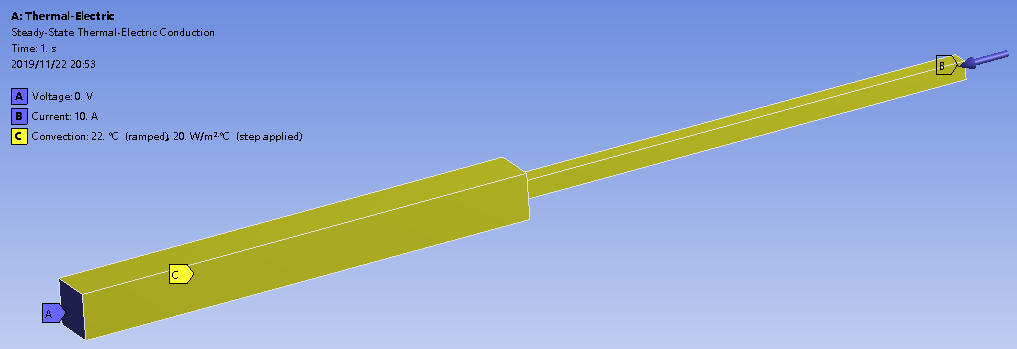
      对导体的一端施加电压边界，电压值0V，对另一端时间电流边界，电流值10A；

设置导体周围为对流边界，对流换热系数20W/m²℃，环境温度22℃。

当导体周围的流体域也考虑进来时，对流换热系数和环境温度都是计算结果，问题变成热电流耦合问题，我们在以后的案例中进行演示。

其他未设置的面为绝缘和绝热边界。

4 计算结果

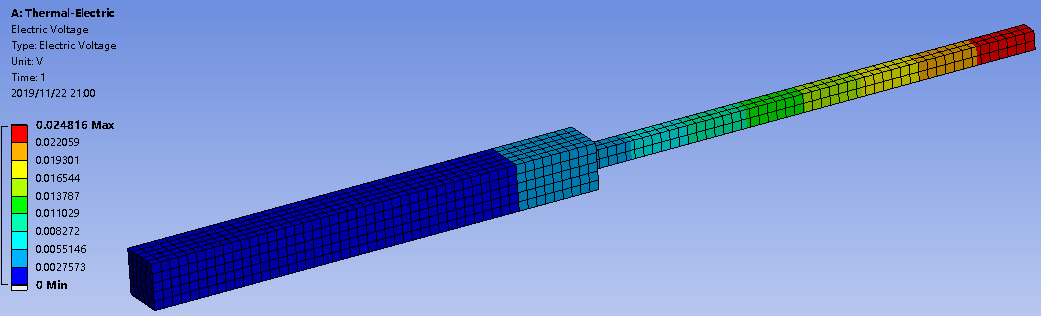
      导体的电压分布如下图，可以看出两端的电压为0.0248V。

我们通过手算计算一下，电阻根据公式R=ρL/s计算，其中ρ为电阻率，L为导体长度，s为导体截面积。

本案例两端截面不同的导体相当于串联，因此可以很容易求得两端的电阻为0.002465Ω。

于是，两端的电压根据U=IR计算得0.02465V，与模拟值相差0.6%。

      电流密度分布如下图，由于总电流I=10A，因此电流密度为总电流除以截面积，截面积小对应的电流密度大。

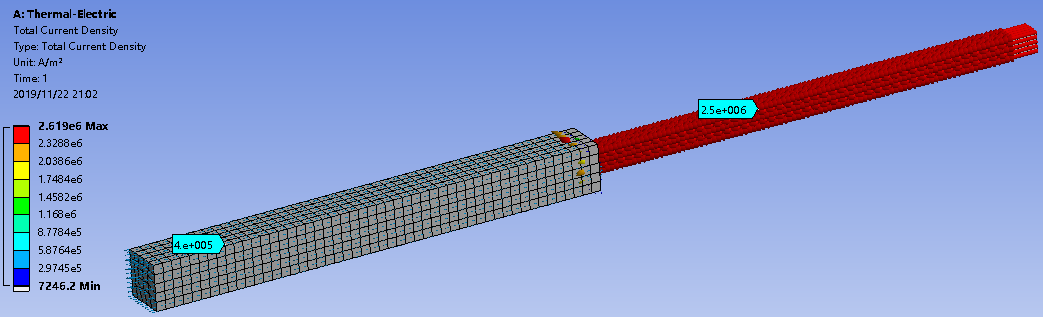
      焦耳热分布如下图，公式Q=I²R可求得发热功率，除以导体的体积即为体积热流密度。

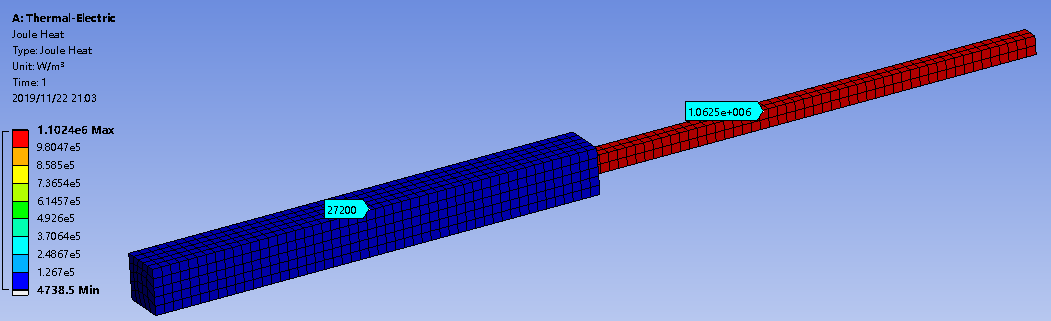
      温度分布如下，可以看出截面积小的导体，由于体积热流密度更大，热量集中，其温度相对更高。

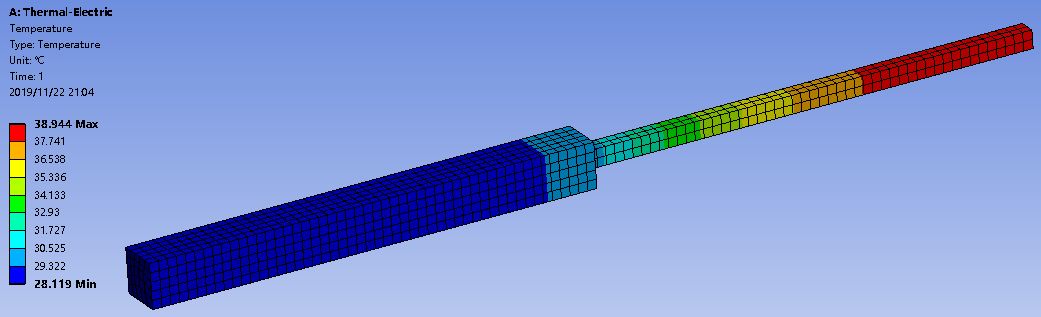
免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删