Lumerical单光子雪崩二极管仿真入门

01 说明

二次光子在单光子雪崩探测器（SPAD）的雪崩过程中被发射，它们对内部和外部串扰都会有影响。在本例中，我们演示了如何计算SPAD中二次光源的位置与测量显微镜物镜之间的传递函数。这个传递函数是一个当我们结合远场测量的二次发射光谱时，允许我们计算SPAD里二次光子产生光谱的校正因子。此外，案例还演示了如何矫正模拟出来的远场功率以涵盖正确的光子产生光谱。最后，我们演示了如何在同一SPAD中执行外部光吸收仿真。

02 综述

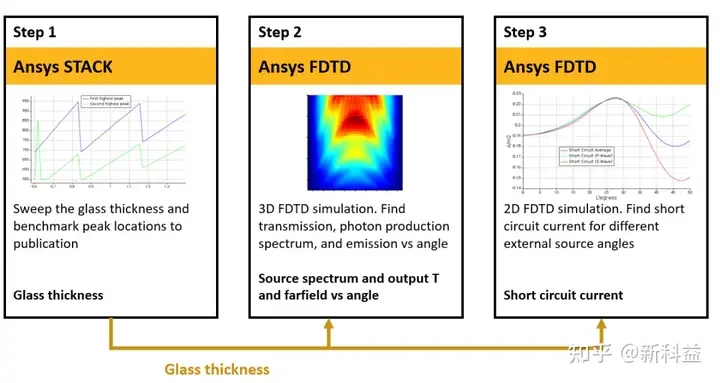
步骤1 使用STACK模拟校正因子以找到初始参数

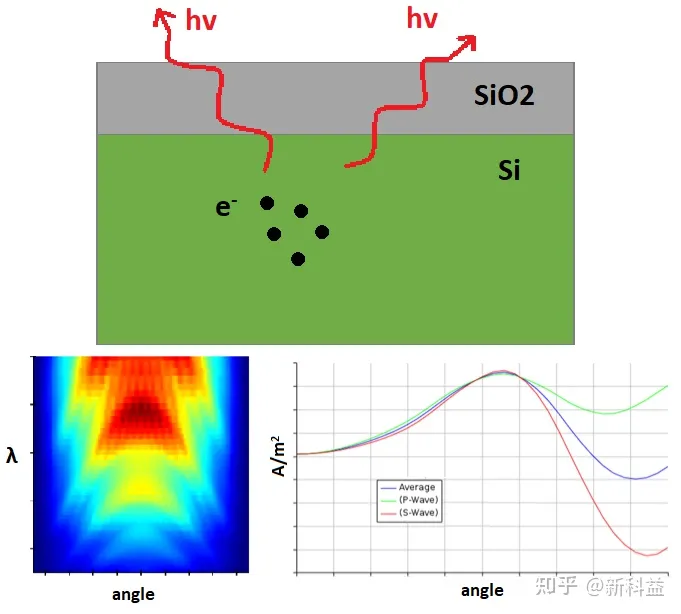
在本例中，我们考虑下图中的空气/SiO2/Si结构，其中光在Si层中产生。

SPAD结构的SiO2层对校正因子的影响较大。Si与SiO2和SiO2与空气之间的反射与波长和角度相关。从光源发出的光在到达SiO2层之前，在Si中会有衰减。较厚的SiO2层产生的干涉图案与厚度有关。因此在不知道SiO2的真实厚度的情况下，该步骤侧重于通过将测量的干涉图案[1]与仿真所得的干涉图案进行匹配来分析出具体厚度。

注意，此步骤用来拟合SiO2厚度值并再现测量的干涉图案，这是因为我们没有本示例中使用的器件的可靠厚度值。如果您已经知道器件的所有相关参数，则可以跳过此步骤。

光是由高场区（上图中的星点）的电子雪崩产生的。其在发射到空气之前会先穿过Si和SiO2层，因此会在通过不同层之间的反射和在Si中被吸收而损失。光在远场中的表现需要考虑显微镜物镜的有限数值孔径。此外，STACK仿真还考虑了SiO2层厚的干扰效应。然而，SiO2层的实际厚度不是很清楚，但可以作为仿真的输入参数。

下图我们可以看到参考文献[1]中进行的发射光测量；这可以用作拟合SiO2厚度的目标结果：

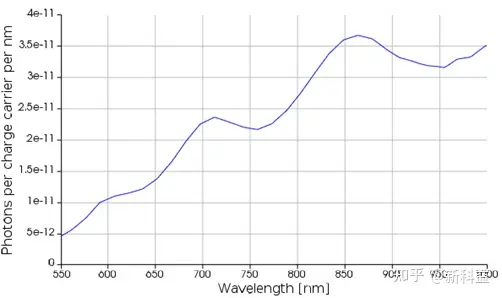
在公布的数据中，两个最突出的峰位于701 nm和859 nm。STACK仿真扫描产生不同SiO2厚度下的透射。对不同SiO2厚度得出的结果使用预设的findpeaks脚本命令来寻找数据中找到峰值：

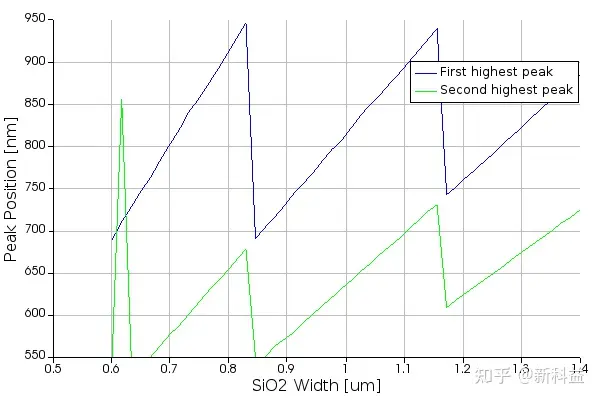
下图显示了作为SiO2厚度的函数的最高两个峰的位置。我们可以估算出SiO2厚度为1.34um，因为它与公布的数据最吻合。

我们可以通过检查测量和仿真的两个最高峰值之间的相对误差来确认这一点：

上图显示了SiO2厚度测量与仿真的最高峰值和第二最高峰值的相对误差。该方法表明，光谱数据在1.34μm至1.36μm范围内匹配较为良好。

步骤2：使用3D FDTD仿真校正因子以获得光子产生曲线

将步骤1中发现的厚度用于3D FDTD SPAD的仿真，求解出传递函数、光子产生曲线以及光源发射角度和频率的关系。通过测量光谱与传递函数的比值，得到真实光子产生曲线。然后，该光子产生的光谱用于矫正远场模拟功率，并获得二次发射与角度的关系，当对覆盖显微镜物镜的角度，进行积分时，二次发射与测量值匹配。

STACK仿真提供了SiO2厚度的初始评估，但由于STACK和FDTD之间的结果差异较小，3D FDTD模拟中使用的实际厚度可能需要进一步调整。如果几何体允许，首先运行STACK仍然可以在缩小参数空间方面节省大量模拟时间。在该示例中，最终SiO2厚度被设置为1.33um以匹配干涉图案。

传递函数、光子产生光谱和发射角分别如下图所示：

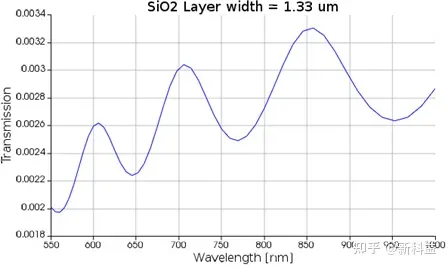
3D FDTD仿真得出的传输效率曲线。从另一个角度，y轴也可以表示光子离开雪崩区域并到达显微镜物镜的概率。

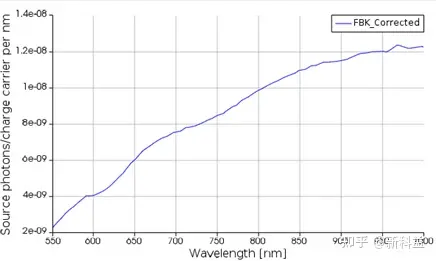
3D FDTD仿真得出的传输效率曲线。从另一个角度，y轴也可以表示光子离开雪崩区域并到达显微镜物镜的概率。

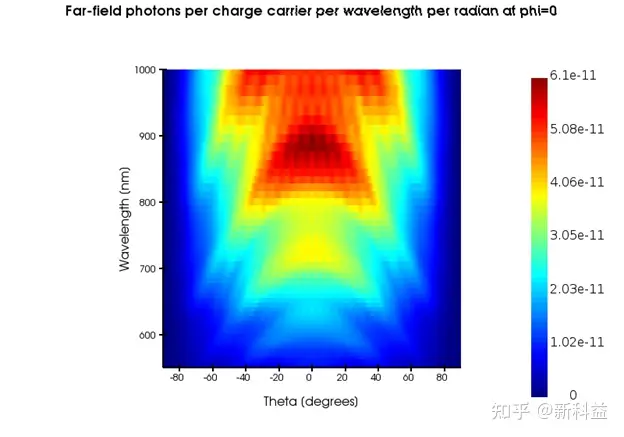
在θ上积分该角度分辨功率，并假设方位角phi对称，将得到测量的二次发射光谱。

步骤3：计算吸收与外部源角度

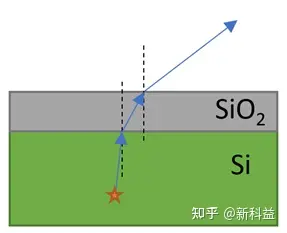
使用步骤1中创建的参数，我们可以模拟SiO2厚度的设计含义。该步骤计算由于外部光吸收引起的短路电流，作为平面波源角度的函数，不包括雪崩倍增增益。

现在可以收集有关进入SPAD器件的光的信息。表征SiPM器件的一个重要参数是以从法线到表面测量的入射角度与光的短路电流的关系。用2D FDTD进行模拟的结果如下所示：

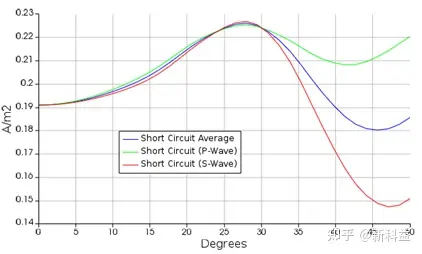
700 nm波长下，短路电流与入射角度的关系。FDTD仿真吸收电流不考虑倍增增益。

翻译：摩尔芯创-BOB