利用Matlab解决数学建模中的最优化问题

1.线性规划

matlab中线性规划优化计算方法和实例

在matlab中用于线性规划优化计算的是linprog()函数。 公式:[x,fval,exitflag,output,lambda]=linprog(c,A,b,Aeq,beq,lb,ub,x0); %x:表示最优解，fval:表示目标函数最优值，exitflag:表示求解的结果是成功还是失败，1代表成功。 %output优化过程中的各种输出信息，lambda：结构体，包含最优解处的拉格朗日乘子。 %c:目标函数系数矩阵，如果求最小值，那么c就是各个变量的系数，如果求最大值，那么c就是各个变量的系数的相反数，A:不等式约束的系数矩阵，b:不等式约束的常向量。 %Aeq:等式约束的系数矩阵，beq：等式约束的常向量，lb、ub表示自变量的上下范围。 %x0:表示变量的初始值，可以缺省。

线性规划优化计算求最优解的方法很多，有单纯形法，大M法，内点法等，linprog函数集中了这几种线性规划算法。

例1：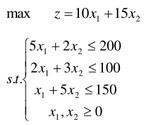

>> c=[-10;-15];
>> A=[5,2;2,3;1,5];
>> b=[200;100;150];
>> lb=[0;0];
>> ub=[];
>> [x,fval]=linprog(c,A,b,[],[],lb,ub)

Optimal solution found.


x =

    7.1429
   28.5714


fval =

 -500.0000

例2：

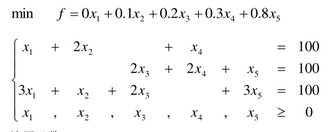
>> c=[0;0.1;0.2;0.3;0.8];
>> aeq=[1,2,0,1,0;0,0,2,2,1;3,1,2,0,3];
>> beq=[100;100;100];
>> lb=[0;0;0;0;0];
>> [x,fval]=linprog(c,[],[],aeq,beq,lb)

Optimal solution found.


x =

   30.0000
   10.0000
         0
   50.0000
         0


fval =

    16

上面解决了简单的线性规划问题的求解，线性规划有两种比较特殊的情况，即整数规划和0-1整数规划。(在旧版本中的matlab是不能直接求解这两种特殊的的线性规划。bintprog函数可以用来求0-1整数规划，但求解过程比较麻烦，而且最新版的matlab已经遗弃了这个函数，同时提供了一个比较新的函数——intlinprog)

公式：[x,fval,exitflag]=intlinprog(c,intcon,A,b,Aeq,beq,lb,ub) %该函数的使用和linprog函数的使用十分相似，其仅仅在linprog函数的基础上多了一个参数——intcon。

通过一个例子来了解一下该函数的用法：

在这个例子中，变量的取值范围不再是有理数集，而是整数集。

>> c=[-1;-1];
>> intcon=[1,2];%intcon为整数约束变量的位置。
>> b=[-1;11;-1];
>> c=[-1;-1];
>> intcon=[1,2];
>> a=[-4,2;4,2;0,-2];
>> b=[-1;11;-1];
>> lb=[0;0];
>> [x,fval]=intlinprog(c,intcon,a,b,[],[],lb)

x =

     2
     1


fval =

    -3

求解0-1整数规划时，只需要在求解整数规划的基础上加上一个对变量的最大值约束为1就行了。
看一个例子

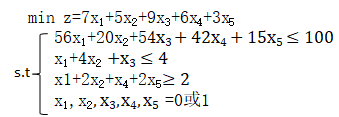
>> c=[7;5;9;6;3];
>> intcon=[1,2,3,4,5];
>> a=[56,20,54,42,15;1,4,1,0,0;-1,-2,0,-1,-2];
>> b=[100;4;-2];
>> lb=[0;0;0;0;0];
>> ub=[1;1;1;1;1];
>> [x,fval]=intlinprog(c,intcon,a,b,[],[],lb,ub)
LP:                Optimal objective value is 3.000000.                                             




     0
     0
     0
     0
     1


fval =

     3

2.二次规划

matlab中二次规划优化计算方法和实例

   什么是二次规划？
· 非线性规划的目标函数自变量为x的二次函数；
· 约束条件全是线性的；

在matlab中用于二次规划优化计算的是quadprog()函数。 公式：[x,fval,exitflag,output,lambda]=quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options) %上述参数与线性规划中的参数含义相同，H为实对称矩阵，在求解前需要把二次规划化为标准形式。

   下面通过两个例子来看一次如何通过matlab求解二次规划

   例1：

>> H=[4,-1;-1,2];
>> f=[-3;-5];
>> a=[1,1;-1,2];
>> b=[5;4];
>> lb=[0;0];
>> [x,fval]=quadprog(H,f,a,b,[],[],lb)




x =

    1.5714
    2.7857


fval =

  -10.3214

从而原问题的最优值为：-10.3214

   例2：

>> H=[2,1,1;1,2,0;1,0,2];
>> f=[-5;-3;-6];
>> a=[5,4,7];
>> b=[22];
>> lb=[0;0;0];
>> [x,fval]=quadprog(H,f,a,b,[],[],lb)

x =

    0.5725
    0.9237
    2.2061


fval =

  -11.0305

原问题的最优值为：11.0305

3.非线性规划

在matlab软件中，函数fmincon用于求解非线性规划问题。 [x,fval,exitflag,output,lambda,grad,hessian]=fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options) %nonlcon表示非线性约束条件(需要写自定义函数)，x0为初值。

   例1：

%编写目标函数
function f=fun1(x)
f=exp(x(1))*(x(1)^2+2*x(2)^2+3*x(1)*x(2)+5*x(1)+4*x(2)+2);
%编写非线性约束条件函数
function[c,ceq]=fun2(x)
c=[3+x(1)*x(2)-x(1)-x(2);x(1)*x(2)-12];
ceq=[];
%编写主程序
>> Aeq=[1,2];
>> beq=[0];
>> x0=[-1;1];
>> [x,fval]=fmincon(@fun1,x0,[],[],Aeq,beq,[],[],@fun2)
%运行结果

x =

   -3.0000
    1.5000


fval =

   -0.3485

fmincon函数是默认从给定的x0为中心开始搜索，直至找到函数的z最小值，并返回距离x0最近的函数最小值对应的值,在计算的时候就必须预先判定函数最小值的对应的x值的大概范围,确保定的初值x0在所求的x附近，以减少计算量。 在利用调用f（x）就可以求得最小值了 如果给的是周期函数 那给不同的值一般应该会得到不同x值 但应该f（x）值是一致的

例2：

%编写目标函数
function f=fun1(x)
f=-0.201*x(1)^4*x(2)*x(3)^2/10^7;
%编写非线性约束条件函数
function[c,ceq]=fun2(x)
c=[x(1)^2*x(2)-675;x(1)^2*x(3)^2/10^7-0.419];
ceq=[];

>> x0=[4;5;50];
>> lb=[0;0;0];
>> ub=[36;5;125];
>> [x,fval]=fmincon(@fun1,x0,[],[],[],[],lb,ub,@fun2)
%运行结果
x =

   28.0299
    0.8591
   73.0273


fval =

  -56.8478

fmincon求解优化问题，最优解不一定唯一。选择不同的迭代初始值x0，可能得到不同的局部最优解(局部最优解不一定为全局最优解)

   例3

%编写目标函数
function f=fun1(x)
f=-(x(2)+x(1)*cos(x(3)))*x(1)*sin(x(3));
%主程序
>> Aeq=[2,1,0];
>> beq=[100];
>> lb=[0;0;0];
>> ub=[100;100;pi/2];
>> x0=[25;20;1];
>> [x,fval]=fmincon(@fun1,x0,[],[],Aeq,beq,lb,ub)
%运行结果
x =

   33.3333
   33.3333
    1.0472


fval =

  -1.4434e+03

4.无约束优化

一、无约束一元函数最优解

在matlab中用于一元无约束优化计算的是fminbnd()函数。 公式：[x,fval,exitflag,output]=fminbnd(fun,x1,x2,options)

例：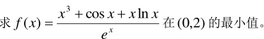

>> f=@(x)(x^3+cos(x)+x*log(x))/exp(x);
>> [x,fval]=fminbnd(f,0,2)

x =

    0.5223


fval =

    0.3974

二、无约束多元函数最优解

在matlab中用于多元无约束优化计算的是fminunc()函数fminsearch函数。 公式[x,fval,exitflag,output,grad,hessian] =fminunc(fun,x0,options) 公式[x,fval,exitflag,output]=fminsearch(fun,x0,options) 当目标函数阶数大于2时，fminunc()比fminsearch()更有效；当目标函数高度不连续时，fminsearch()更具稳健性。

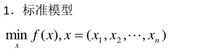
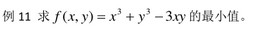
>> f=@(x)x(1)^3+x(2)^3-3*x(1)*x(2);
>> [x,fval]=fminunc(f,[0.5,3])


x =

    1.0000    1.0000


fval =

   -1.0000

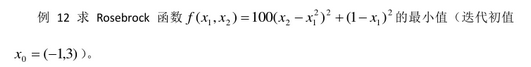
>> f=@(x)100*(x(2)-x(1)^2)^2+(1-x(1))^2;
>> [x,fval]=fminsearch(f,[-1,3])

x =

    1.0000    1.0000


fval =

   1.4253e-10

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删