MATLAB在优化问题中的应用探索

1.无约束的优化问题

fminbnd fminsearchfminunc  %求解不连续的函数极值问题效果不佳fminimax以及fmincon % 解决有约束的问题，被称作万能函数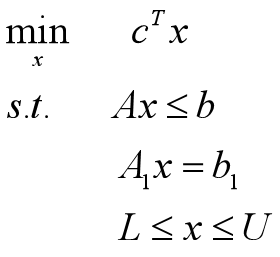

2.有约束的优化问题

(1)线性规划

一般形式

例：

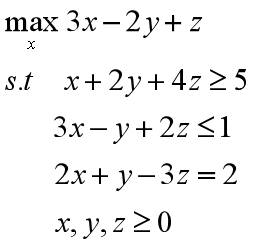
标准形式为：

matlab求解

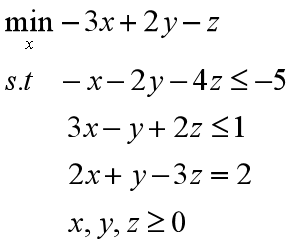
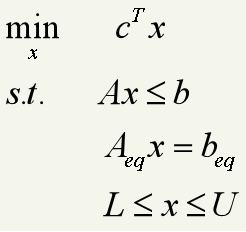
针对上边的标准形式，matlab的求解函数为linprog 调用格式为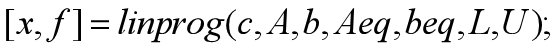

注意：当函数后面的参数缺失时，可以直接略去，如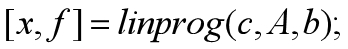

但缺失中间的参数，需要用空数组符号[]补位。如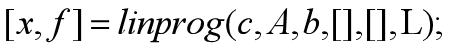

例：求解线性规划问题

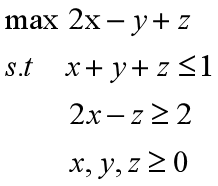
解：

(1)化为标准形式

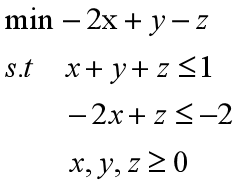
(2)写成矩阵形式

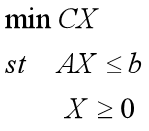
其中

C=[-2,1,-1]; A=[1,1,1;-2,0,1]; b=[1;-2];

代码：

C=[-2,1,-1];A=[1,1,1;-2,0,1];b=[1;-2]; X=linprog(C,A,b,[],[],zeros(3,1))

(2)混合数学规划问题

当线性规划模型中存在整数变量，则称为整数规划模型或混合规划模型。

在整数变量中，一种重要的整数变量是0-1变量，它在处理定性的量中有重要应用。

线性整数规划求解的matlab函数为 X=intlinprog(c,intcon,A,b,A1,b1,L,U);

函数的参数与linprog相同，只是在c后面添加参量intcon，用来指示哪些变量是整数变量。如intcon=[2,3]表示第2,3个变量是整变量。

例：计算

f=[8,1];intcon=[2];A=[-1  -2   -4  -1    2   1];b=[14;-33;20];L=[0;0];x=intlinprog(f,intcon,A,b,[],[],L)

01整数规划

例：某企业拟在8个居民区A1,A2,…,A8建若干个门店，门店的备选地址有B1,B2,…,B6。各备选地址能覆盖的居民区如下表：

如何选址，可以用最少的门店覆盖所有居民区

解：

(1)决策变量：决策是门店选址，应使用0-1变量 ，xi=1,即选择Bi,i=1,2,…,6

(2)目标：总门店数最少，即 min   x1+x2+…+x6

(3)约束条件：

1. 覆盖A1:   x1+x2+x3>=1
2. 其他类似：x2+x4>=1
3. x3+x5>=1
4. x4+x6>=1
5. x1+x2+x3+x5>=1
6. x5+x6>=1
7. x1>=1
8. x2+x4+x6>=1

代码：

c=ones(6,1); intcon=1:6;A=[1  1  1  0  0  0      0  1  0  1  0  0      0  0  1  0  1  0      0  0  0  1  0  1      1  1  1  0  1  0      0  0  0  0  1  1      1  0  0  0  0  0      0  1  0  1  0  1];b=ones(8,1);x=intlinprog(c,intcon,-A,-b,[],[],zeros(6,1), ones(6,1))

(3)二次规划

当目标函数是二次函数时，数学规划称为二次规划 二次规划的标准形式如下（目标函数为二次，约束条件为线性）

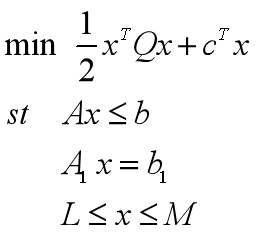
x = quadprog(H,f)x = quadprog(H,f,A,b)x = quadprog(H,f,A,b,Aeq,beq)x = quadprog(H,f,A,b,Aeq,beq,lb,ub)x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0)x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options)求解非线性规划问题：min 1/2*x’*H*x,  A*x ≤ b, Aeq*x = beq；lb ≤ x ≤ ub；

注意：H 为二次型系数矩阵

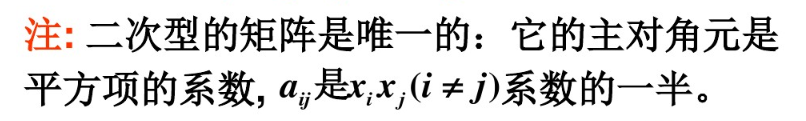
例：解下列二次规划

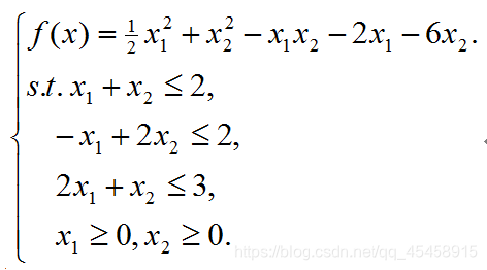
H = [1 -1; -1 2];f = [-2; -6];A = [1 1; -1 2; 2 1];b = [2; 2; 3];lb = zeros(2,1);opts = optimoptions('quadprog','Algorithm','active-set');[x,fval] = quadprog(H,f,A,b,[],[],lb,[],[],opts)

(4)非线性规划

Matlab中的非线性规划为以下规范形式：

函数形式：[x,f] = fmincon(fun,x0,A,b,Aeq,beq, L, U, nonlcon)

x=fmincon (fun, 初值, A, b )x=fmincon (fun, 初值, A, b, Aeq，beq )x=fmincon (fun, 初值, A, b, Aeq, beq, lb, ub )x=fmincon (fun, 初值, A,b,Aeq,beq,lb,ub,nonlcon, options) 

fun写成如下的M-函数形式 (objfun.m) :

function  f = objfun (x)

   f = f(x);

end

非线性约束条件写成如下的M-函数形式

function [c,ceq]=nonlcon(x)

   c = c(x);

   ceq=ceq(x);

end

[x, f]=fmincon (...)同时返回解x处的函数值

例：

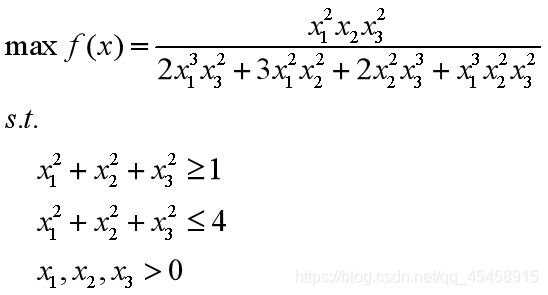
解：

第一步，化为标准形式，这里约束条件无线性函数，也无等式约束

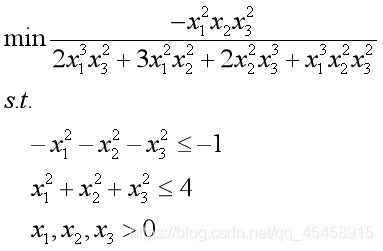
第二步，在 editor窗口写目标函数，保存

function f = objfun(x)f = -x(1)^2*x(2)*x(3)^2/(2*x(1)^3*x(3)^2+3*x(1)^2*x(2)^2+2*x(2)^2*x(3)^3+x(1)^3*x(2)^2*x(3)^2); end

第三步，在 editor窗口写非线性约束函数，保存

function [c, ceq] = nonlincon(x)c=[-x(1)^2-x(2)^2-x(3)^2+1; x(1)^2+x(2)^2+x(3)^2-4];ceq = [ ];end

第四步，在commond window求解

options = optimset('Algorithm', 'interior-point', 'Display', 'off'); %设置算法 [x,fval] = fmincon(@objfun, [1,1,1],[],[],[],[],[0,0,0],[],@nonlincon, options)

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删