MATLAB在信号与系统中的应用探索

MATLAB 信号与系统

1 信号的Matlab表示与绘图

1.1 连续信号的绘制

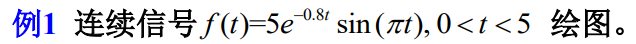
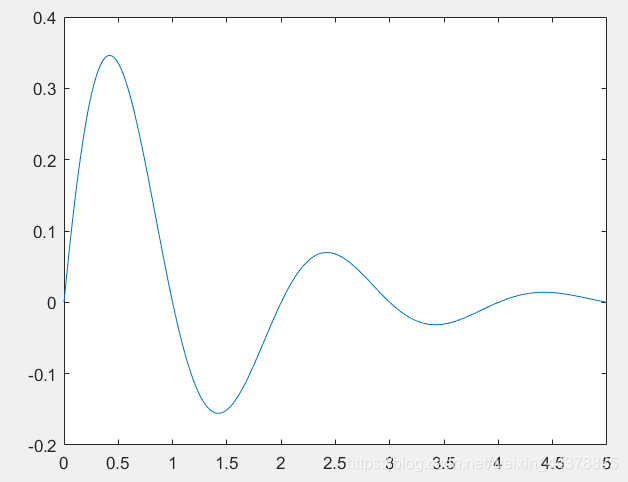
b=0.5;
a=0.8;
t=0:0.001:5;
x=b*exp(-a*t).*sin(pi*t);
plot(t,x)   % 绘制波形

1.2 离散信号的绘制

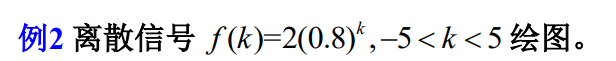
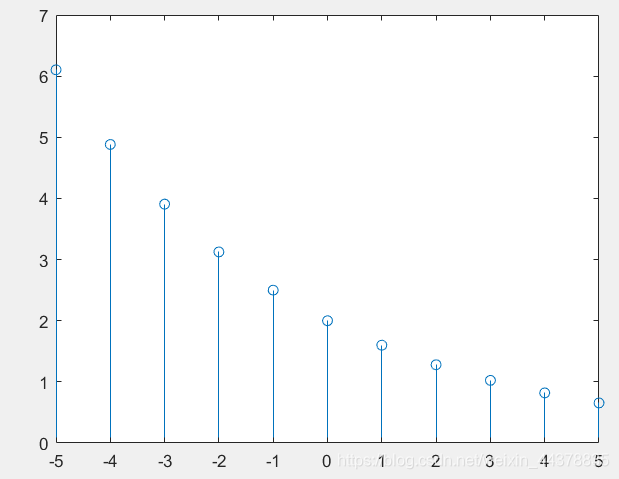
c=2;
d=0.8;
k=-5:5;
y=c*d.^k;
stem(k,y);  % 绘制波形

2 Matlab求解系统的响应

求LTI系统的零状态响应的函数lsim，其调用格式为

式中，t表示计算系统响应的抽样点向量；f是系统输入

   信号，sys是LTI系统模型，用来表示微分方程。

系统模型sys要借助tf函数获得，其调用方式为

sys=tf(b, a)

式中，b和a分别为微分方程的右端和左端各项的系数。

   比如：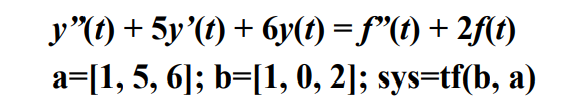

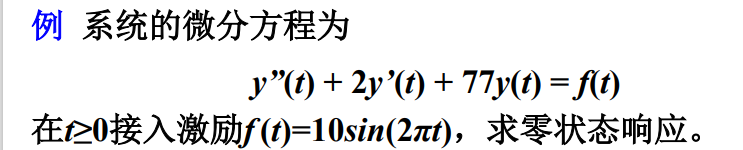
sys=tf([1],[1,2,77]); %　tf函数获得系统模型sys
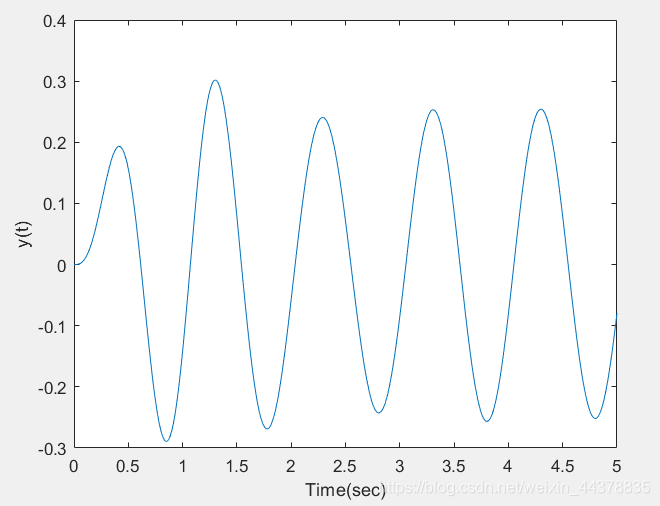
t=0:0.01:5;           % 对时间t进行离散取样
f=10*sin(2*pi*t);     
y=lsim(sys,f,t);      % 求系统的零状态响应
plot(t,y)
xlabel('Time(sec)')
ylabel('y(t)')

3 Matlab求解冲激响应和阶跃响应

MATLAB提供了专门用于求LTI系统的冲激响应和阶跃响应的函数。设LTI系统的微分方程为：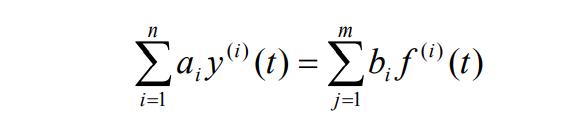


   求LTI系统的冲激响应的函数为：

impulse(b, a)

求LTI系统的阶跃响应的函数为：

step(b, a)

其中a和b表示系统方程左端和右端的系数向量。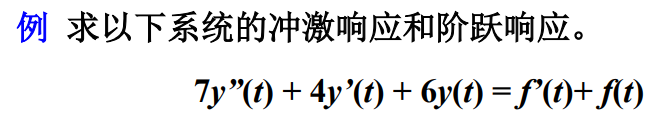

a=[7,4,6];
b=[1,1];
subplot(2,1,1)
impulse(b,a);
subplot(2,1,2)
step(b,a)

4 卷积的Matlab求解

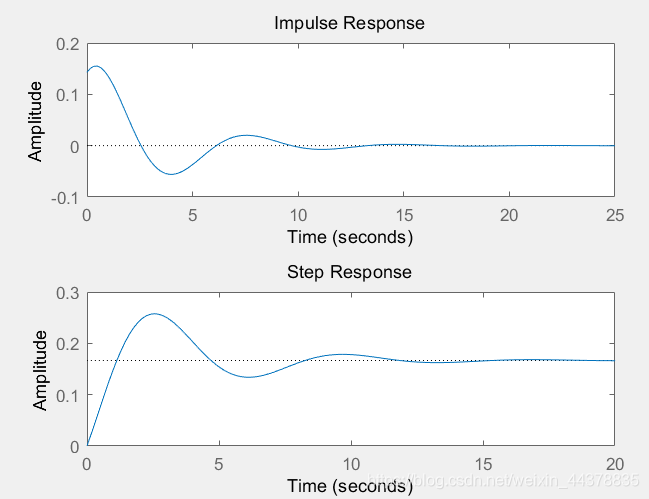
MATLAB处理离散卷积的函数为conv(f1, f2)，对序列做卷积运算。

   处理连续信号的卷积时，需要对连续信号取相同的卷积步长，结果再乘以实际步长（连续信号的取样间隔；采样点越多，值越大）。

t11=0;t12=1;t21=0;t22=2;
%f1(t)
t1=t11:0.001:t12;
ft1=2*rectpuls(t1-0.5,1); %幅值为1，宽度为1，t1=0.5点对称的方波信号
%f2(t)
t2=t21:0.001:t22;
ft2=t2;
t3=t11+t21:0.001:t12+t22;
ft3=conv(ft1,ft2);
ft3=ft3*0.001;  % 取1000个样点之和，因此需要*0.001
plot(t3,ft3)
title('ft1(t)*ft2(t)')

5 Matlab求解离散系统的零状态响应

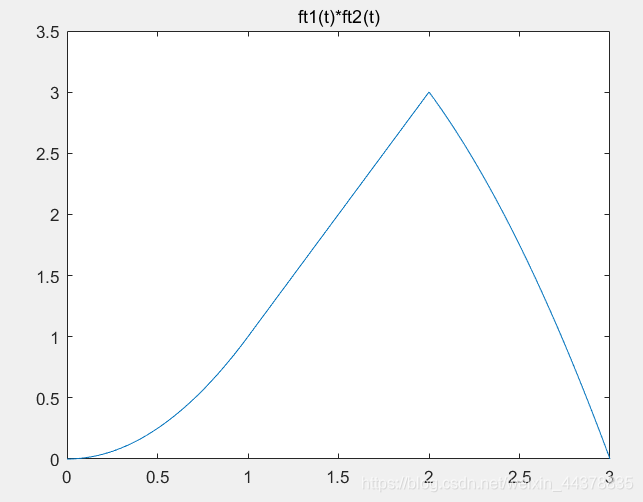
在零状态时，MATLAB工具箱提供了一个filter函数，计算由差分方程描述的系统响应，其调用格式为

y=filter(b,a,f)

其中b=[b0,b1,b2,…, bm]，a=[a0,a1,a2,…, an]分别是差分方程左右的系数向量，f表示输入序列，y表示系统的零状态响应。注意输出和输入序列的长度相同。

R=51;
d=rand(1,R)-0.5;
k=0:R-1;
s=2*k.*(0.9.^k);
f=s+d;
figure(1);
stem(k,f,'.');
M=5;
b=ones(M,1)/M;
a=1;
y=filter(b,a,f);
figure(2)
stem(k,y,'.')

6 Matlab求解单位脉冲响应

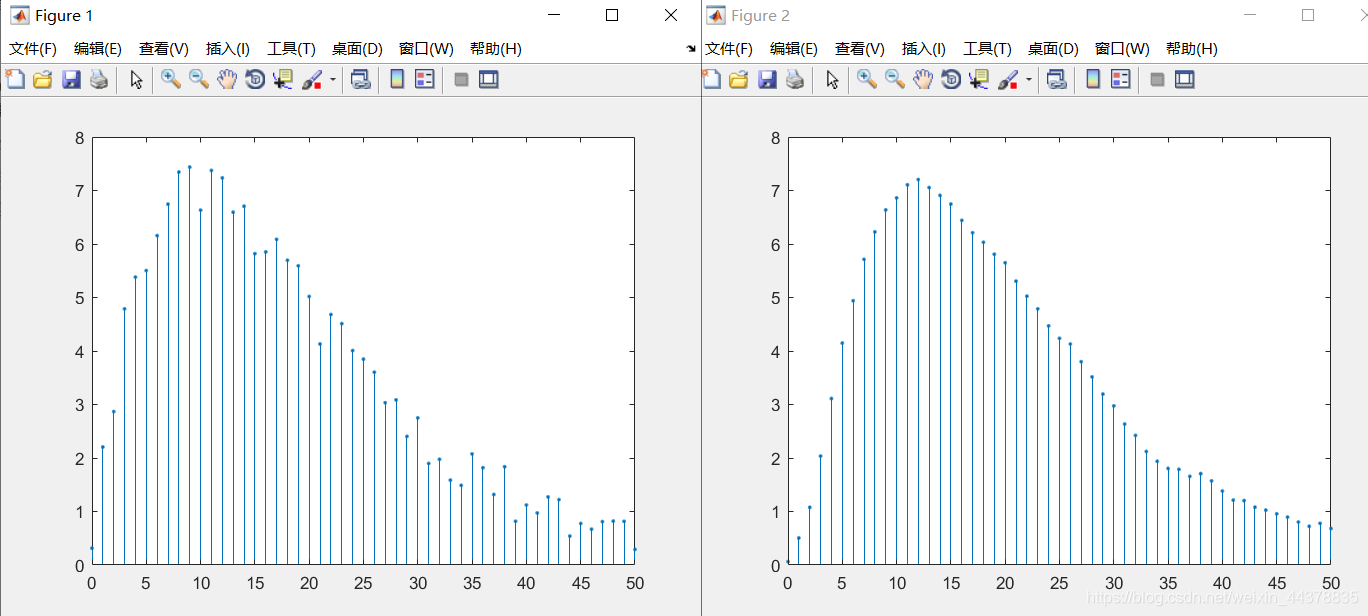
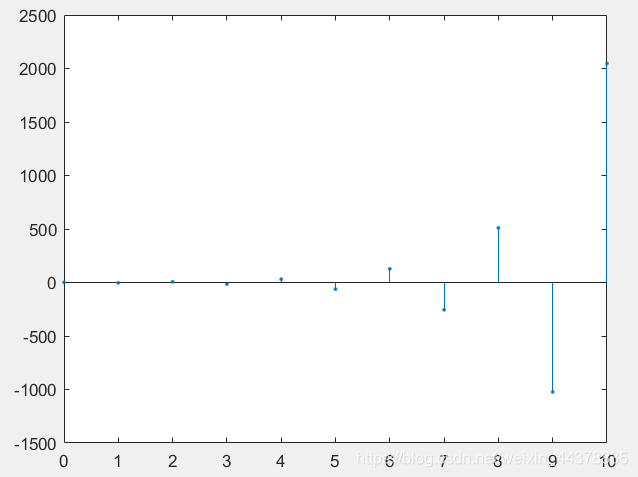
MATLAB提供了专门用于求LTI离散系统的单位脉冲响应的函数：

h=impz(b,a,k)

其中a=[a0,a1,a2,…, an]，b=[b0,b1,b2,…, bn]分别是差分方程左右的系数向量，k表示输出序列的取值范围，h就是系统的单位脉冲响应。

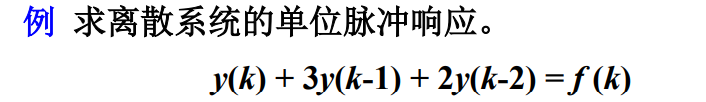
k=0:10;
a=[1,3,2];  
b=[1];
h=impz(b,a,k);
stem(k,h,'.')

7 卷积和的Matlab求解

MATLAB中用于计算离散序列卷积的函数为：

conv(x1,x2)

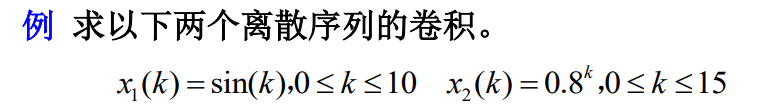
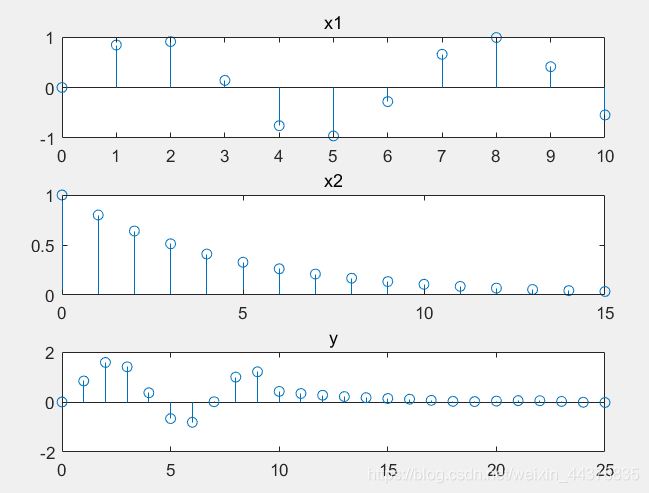
k1=0:10;
x1=sin(k1);
k2=0:15;
x2=0.8.^k2;
y=conv(x1,x2);
subplot(3,1,1)
stem(k1,x1,'o')
title('x1')
subplot(3,1,2)
stem(k2,x2,'o')
title('x2')
subplot(3,1,3)
stem(0:25,y,'o')
title('y')

8 Matlab求解系统响应

t=0:pi/100:4*pi;
b=[-1,1]; %频率响应函数的分子系数
a=[1 1]; %频率响应函数的分母系数
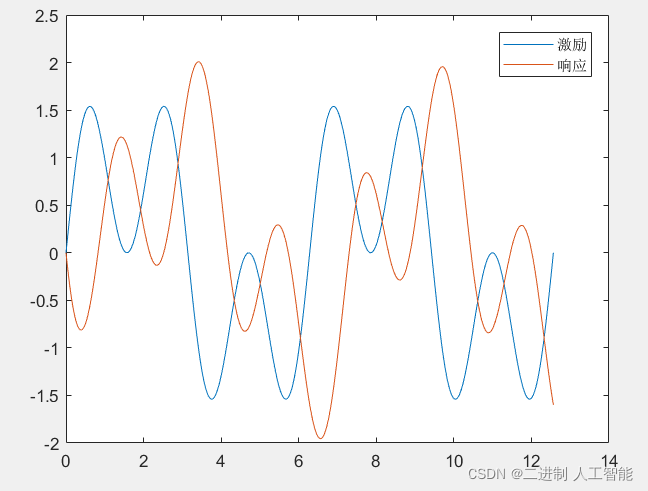
ft=sin(t)+sin(3*t); % 激励
yt=lsim(b,a,ft,t); %求解响应
plot(t,ft,t,yt)
legend('激励','响应')

z变换的MATLAB计算

MATLAB内置了符号函数ztrans 和iztrans函数分别对应 z变换和逆z变换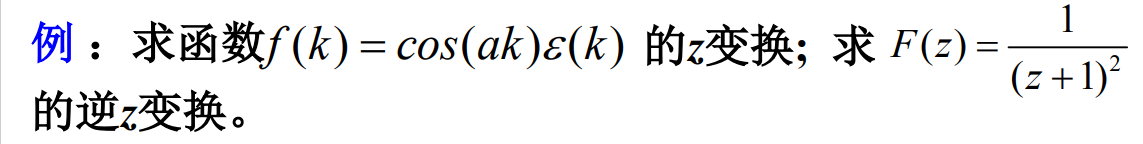

f=sym('cos(a*k)');
F=ztrans(f)

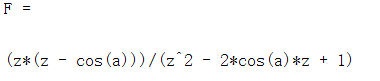
F=sym('1/(1+z)^2');
fInver=iztrans(F)

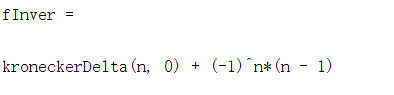
免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删