计算机视觉全攻略：SLAM概率模型与EKF

Simultaneous Localization and Mapping

SLAM是一种同时完成定位与创建地图的技术。定位和地图是一个典型先有鸡还是先有蛋的问题，通常地图是定位的前提，而地图的创建又需要好的位置估计。以下内容包括SLAM问题定义和经典EKF SLAM算法。后续会写Graph-based SLAM(PTAM)与ORB-SLAM。

地图分类

常见地图分为三类，基于网格的地图，基于特征的地图，基于拓扑的地图。

• 网格地图。将地图分成网格，机器人在离散的空间上定位，计算复杂度取决于网格的大小和精度。
• 特征地图。基于特征的地图由路标(landmark)构成。计算复杂度由路标的个数决定。
• 拓扑地图。通常在拓扑节点空间上定位。计算复杂度最小。

SLAM问题

上面两幅图以特征(Feature-based地图为例分别描述了一个简单里程计(轮速仪)和SLAM算法工作过程。蓝色的星标代表landmark，红色三角形代表机器人当前的pose，粉红色三角形代表机器人的历史pose，灰色椭圆形表示机器人pose的概率分布，橙色椭圆形表示landmark的概率分布。

• 传统的里程计算法(轮速仪)只估计机器人的位姿(pose)。随着时间的推移，pose估计会产生越来越大的累积误差。
• SLAM同时估计Location(Pose)与Map (landmark)，并建立历史Pose与历史Landmark坐标之间的关联从而提升机器人Pose与Landmark（地图）的准确性。
• 如上图右所示，机器人在位置1出发，定义此位置为已知量，因此可以认为此时pose没有误差(红色三角上没有灰色椭圆)。机器人在此位置观测到了两个landmark。由于观测模型误差的存在，每个landmark都存在不确定性。(两个小的橙色椭圆)。
• 机器人前进到位置2。此时，由于运动模型误差，机器人pose估计有了不确定性(灰色椭圆)。同时，观测到两个新的landmark。这时的观测误差叠加了观测模型和运动模型的误差，因此，增加了不确定性（橙色椭圆个头比之前大）。
• 机器人在位置2同时观测到了之前的那两个landmark。建立四个landmark与两个pose的相关性，从而减少他们的不确定性。(图中所有椭圆变小）。

上面两幅图只是简单的图示，而不能作为区别里程计与SLAM的依据。联系之前文章提到的视觉里程计算法(VO)，有许多优秀的算法采用了基于窗口的Bundle Adjustment，同时估计了landmark与pose。 里程计算法(VO)与SLAM的区别体现在哪里？ 目的不同。VO只关注机器人的pose甚至只关注两帧之间的位置变化，而SLAM在计算pose的同时还需要创建地图。 优化范围不同。与SLAM类似，VO算法也可以采用Bundle Adjustment与Pose-graph优化，但他的优化范围是基于窗口的，属于局部的，而SLAM优化的最终目的是全局地图。 SLAM算法通常会采用long term loop closure算法。当探测到当前位置曾经来过的时候(形成了loop)，SLAM算法会根据历史信息，更新概率模型的先验数据，从而进一步降低整个路径的不确定性。 传送门 ：视觉里程计综述

概率模型

SLAM问题可以建模成一个条件概率问题。

公式化这个模型，如上图所示，

• t 时刻，机器人的位姿(pose)为xt   x  t    x_{t}, 0到t时刻的路径可以表示为 {\color{DarkGreen} \left \{ x_{0}, x_{1},\, ...\, , x_{t} \right \}}   {\color{DarkGreen} \left \{ x_{0}, x_{1},\, ...\, , x_{t} \right \}}   {\color{DarkGreen} \left \{ x_{0}, x_{1},\, ...\, , x_{t} \right \}}
• 机器人 t-1 时刻到 t 时刻的运动为ut   u  t    u_{t}, 0到t时刻的运动（控制量）表示为 {\color{Blue} \left \{ u_{0}, u_{1},\, ...\, , u_{t} \right \}}   {\color{Blue} \left \{ u_{0}, u_{1},\, ...\, , u_{t} \right \}}   {\color{Blue} \left \{ u_{0}, u_{1},\, ...\, , u_{t} \right \}}
• 路标的"真实"位置为{\color{Purple} \left \{ m_{0}, m_{1},\, ...\, , m_{t} \right \}}   {\color{Purple} \left \{ m_{0}, m_{1},\, ...\, , m_{t} \right \}}   {\color{Purple} \left \{ m_{0}, m_{1},\, ...\, , m_{t} \right \}}
• 每一时刻t，机器人对能观测到的k个路标的观测值为{\color{Orange} \left \{ z_{0}, z_{1},\, ...\, , z_{k} \right \}}   {\color{Orange} \left \{ z_{0}, z_{1},\, ...\, , z_{k} \right \}}   {\color{Orange} \left \{ z_{0}, z_{1},\, ...\, , z_{k} \right \}}

SLAM求解的是一个条件概率，已知路标的观测z, 机器人的运动(控制)u，估计0到t时刻机器人的pose x，以及路标m的坐标。

                p(x0:t,m0:N|z0:k,u0:t)  p( x  0 : t  , m  0 : N   |  z  0 : k  , u  0 : t  )  p(x_{0:t},m_{0:N}|z_{0:k}, u_{0:t})    

后验概率问题很自然的就想到了Kalman滤波。事实上滤波算法曾一度统治SLAM。

扩展Kalman滤波(EKF)

由于刚体运动的变化(系统模型)与噪声通常不是线性的，因此很多算法采用扩展Kalman滤波(EKF)。

描述机器人pose的状态向量，以3维(x, y, θ)为例，那么3*3的协方差矩阵如下图。

XR=⎡⎣⎢xryrθr⎤⎦⎥   X  R  = [     x  r        y  r        θ  r      ]   X_{R}=\begin{bmatrix} x_{r} \\y_{r} \\ \theta _{r} \end{bmatrix}         Ck=⎡⎣⎢⎢σ2xσyxσθxσxyσ2yσθyσxθσyθσ2θ⎤⎦⎥⎥   C  k  = [     σ  x   2      σ  x y      σ  x θ        σ  y x      σ  y   2      σ  y θ        σ  θ x      σ  θ y      σ  θ   2      ]   C_{k} =\begin{bmatrix} \sigma _{x}^{2} & \sigma _{xy} & \sigma _{x\theta }\\ \sigma _{yx}& \sigma _{y}^{2} & \sigma _{y\theta }\\ \sigma _{\theta x} & \sigma _{\theta y } & \sigma _{\theta}^{2} \end{bmatrix}

SLAM的状态向量 xk   x  k    x_{k} 需要在机器人pose向量的基础上加上路标(landmark)的向量，如下图，

如果使用两个变量(α，γ)表示路标，那么状态向量的长度为3+2n, 协方差矩阵C的大小(3+2n) * (3+2n)。

状态预测

EKF首先需要考虑状态向量的预测。状态预测只更新pose向量及相关的协方差，黄色+绿色标注，

系统方程：x^R=f(xR,u)     x ^    R  =f( x  R  ,u)  \hat x_{R}=f(x_{R},u)  ,    

预测协方差：C^R=FxCRFTx+FuUFTu     C ^    R  = F  x   C  R   F  x   T  + F  u  U F  u   T    \hat C _{R} = F_{x}C_{R}F_{x}^{T}+F_{u}UF_{u}^{T}， C^RMi=FxCRMi     C ^    R  M  i    = F  x   C  R  M  i      \hat C_{RM_{i}} = F_{x}C_{RM_{i}}

f 是系统方程，预测的结果取决于控制量u和上一帧的状态向量。举个例子，如果使用轮速仪，f就是左轮位移，右轮位移与轮距的函数。Fx, Fu为f的雅可比矩阵。CR   C  R    C_{R}为上次估计的协方差矩阵，U为运动模型噪声。

观测预测

z^k=h(x^k)     z ^    k  =h(   x ^    k  )  \hat z_{k} = h(\hat x_{k}),  通过新预测的状态向量，预测观测的值。

观测

zk=[z1z2]   z  k  = [     z  1        z  2      ]   z_{k} = \begin{bmatrix} z_{1}\\ z_{2} \end{bmatrix} ,  观测值直接由传感器获得。  

数据关联(data association)

此处需要额外的算法将预测的观测和传感器的观测建立对应关系。常见的算法有基于2D/3D点的NN, ICP算法，基于图像的特征匹配算法(Sift, Surf, ORB)等。

如果观测zjk   z  k   j    z_{k}^{j} 与观测预测 z^ik     z ^    k   i    \hat z_{k}^{i} 认为是同一路标，计算残差。R为观测噪声。

更新(Update)

计算Kalman增益K，更新状态向量x及协方差矩阵C(下图粉红色）。

加入新观测的路标。

完整的程序框架可参考[1]第十章。

MonoSLAM

[3]MonoSLAM采单目摄像机，基于上文的EKF算法，实现了实时的SLAM。MonoSLAM是开源项目，作者给出了项目源代码SceneLib。

由于历史久远，随着库函数更新以及相机接口更新，GITHUB上有很多改进版本。其中星标最多的是Hanme Kim的版本。

https://github.com/hanmekim/SceneLib2.git

由于MonoSLAM是一个典型的EKF算法，因此只需简单说明一下他的状态向量，观测向量，系统方程和观测方程，其他部分与上文完全相同。以下符号取自论文原文，与上文略有不同。

状态向量

令 x^    x ^    \hat x 为状态向量，包含pose向量x^v     x ^    v    \hat x_{v}与路标向量y^i     y ^    i    \hat y_{i}，协方差矩阵为PP (上文的Ck)

pose向量xv   x  v    x_{v}由13个元素组成，

其中,rw  r w   r^{w}代表了3维位置坐标，qcw  q c w   q^{cw}表示方向四元组（李代数，表示了刚体运动的旋转，将旋转矩阵9个变量缩小为4个），vw  v w   v^{w}为三维空间的线速度，ωc  ω c   \omega ^{c}为三维空间的角速度。

状态模型采用匀线速度，匀角速度模型。每帧考虑一个很小的线速度加速度aw  a w   a^{w}与角速度αw  α w   \alpha ^{w}，他们符合均值为0的高斯分布。

系统方程

根据此函数求雅克比矩阵得残差更新方程，

观测预测

观测预测方程是3D点到2D点的投影。已知更新的相机位置rw  r w   r^{w}，可以计算特征点到相机的距离hRL   h  L   R    h_{L}^{R}。

根据相机投影矩阵，获得特征点在图像上的预测位置。

数据关联

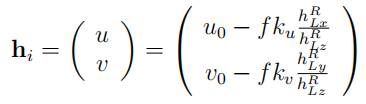
论文采用Shi and Tomasi算法匹配特征点。建立观测与历史观测的对应关系。从而计算残差。

更新

典型的EKF更新。过程见上文。

EKF算法的另一个重要部分就是如何初始化。具体的过程在论文[3]有详细的描述，也可以参考源码。偷个懒，不写了。

EKF的局限

EKF算法非常简单，而且效果在当时也还不错。其衍生出来的各种滤波算法曾经占据SLAM的主导地位，也有一些非常著名的算法如基于粒子滤波的FastSLAM等。然而，EKF仍有很多局限。

• SLAM的EKF算法中状态向量体型较大。与只关注与定位的EKF不同，SLAM状态向量还需要包含路标信息。
• 与之相应的，协方差矩阵体量也很大(N*N)，随着路标的增长，协方差矩阵呈其平方的增长。
• 以上两点带来了计算的复杂度，因此基于EKF的SLAM不适合大场景下的地图创建。即使实时性算法MonoSLAM也仅在一个"room size"的室内环境。
• EKF本身是非线性的一阶线性展开。能否很好的近似整个函数，取决于系统运动模型和观测模型。

虽然EKF SLAM存在这些局限，但其在采用惯导等传感器的算法上仍有很多实际应用。 而视觉SLAM则大多转向了基于图优化的算法(PTAM, ORBSLAM, ...)。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删