模拟退火算法在机器学习中的仿真应用

1.简介

随机寻优算法，其出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。模拟退火算法从某一较高初温出发，伴随温度参数的不断下降,结合概率突跳特性在解空间中随机寻找目标函数的全局最优解，即在局部最优解能概率性地跳出并最终趋于全局最优。模拟退火算法是一种通用的优化算法，理论上算法具有概率的全局优化性能,目前已在工程中得到了广泛应用，诸如VLSI、生产调度、控制工程、机器学习、神经网络、信号处理等领域。

模拟退火算法是通过赋予搜索过程一种时变且最终趋于零的概率突跳性，从而可有效避免陷入局部极小并最终趋于全局最优的串行结构的优化算法。

2.原理

模拟退火算法来源于固体退火原理，将固体加温至充分高，再让其徐徐冷却，加温时，固体内部粒子随 温升变为无序状，内能增大，而徐徐冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，内能减为最小。根据Metropolis准则， 粒子在温度T时趋于平衡的 概率为e(- ΔE/(kT))，其中E为温度T时的内能，ΔE为其改变量，k为Boltzmann常数。在模拟退火算法中，设优化问题的控制参数为时的一个解及其非负目标函数分别与固体的在某一温度下的一个微观状态及其能量等价，设随着算法进程递减其值的控制参数相当固体退火过程中的温度的角色，则对于控制参数的每一取值，算法持续进行"产生新解—判断—接受/舍弃"的迭代过程就对应着固体在某一恒定温度下趋于热平衡的过程，也就是执行了一次Metropolis算法。用固体退火模拟组合优化问题，将内能E模拟为 目标函数值f，温度T演化成控制参数t，即得到解组合优化问题的模拟退火算法：由初始解i和控制参数初值t开始，对当前解重复“产生新解→计算目标函数差→接受或舍弃”的迭代，并逐步衰减t值，算法终止时的当前解即为所得近似 最优解，这是基于 蒙特卡罗迭代求解法的一种启发式 随机搜索过程。退火过程由冷却进度表(Cooling Schedule)控制，包括控制参数的初值t及其衰减因子Δt、每个t值时的迭代次数L和停止条件S。

模拟退火算法的模型

1模拟退火算法可以分解为 解空间、 目标函数和初始解三部分。

2模拟退火的基本思想:

1) 初始化：初始温度T( 充分大)，初始解状态S(是算法迭代的起点)，每个T值的迭代次数L

2) 对k=1, …, L做第(3)至第6步：

3) 产生新解S′

4) 计算增量ΔT=C(S′)-C(S)，其中C(S)为 评价函数

5) 若ΔT<0则接受S′作为新的当前解，否则以概率exp(-ΔT/T)接受S′作为新的当前解.

6) 如果满足终止条件则输出当前解作为 最优解，结束程序。

终止条件通常取为连续若干个新解都没有被接受时终止算法。

7) T逐渐减少，且T->0，然后转第2步。

模拟退火算法的步骤

模拟退火算法新解的产生和接受可分为如下四个步骤：

第一步是由一个产生函数从当前解产生一个位于解空间的新解；为便于后续的计算和接受，减少算法耗时，通常选择由当前新解经过简单地变换即可产生新解的方法，如对构成新解的全部或部分元素进行置换、互换等，注意到产生新解的变换方法决定了当前新解的邻域结构，因而对冷却进度表的选取有一定的影响。

第二步是计算与新解所对应的 目标函数差。因为目标函数差仅由变换部分产生，所以目标函数差的计算最好按增量计算。事实表明，对大多数应用而言，这是计算目标函数差的最快方法。

第三步是判断新解是否被接受,判断的依据是一个接受准则，最常用的接受准则是Metropolis准则: 若ΔT<0则接受S′作为新的当前解S，否则以概率exp(-ΔT/T)接受S′作为新的当前解S。

第四步是当新解被确定接受时，用新解代替当前解，这只需将当前解中对应于产生新解时的变换部分予以实现，同时修正目标函数值即可。此时，当前解实现了一次迭代。可在此基础上开始下一轮试验。而当新解被判定为舍弃时，则在原当前解的基础上继续下一轮试验。

模拟退火算法与初始值无关，算法求得的解与初始解状态S(是算法迭代的起点)无关；模拟退火算法具有渐近收敛性，已在理论上被证明是一种以概率l 收敛于全局 最优解的全局优化算法；模拟退火算法具有并行性。

图2.1 固体退火过程示意图

图2.2 模拟退火算法流程示意图

3.流程图

4.伪代码

5.Metropolis准则——以概率接受新状态

先给定以粒子相对位置表征的初始状态old，作为固体的当前状态，该状态的能量是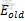。然后用摄动装置使随机选取的某个粒子的位移随机地产生一个微小变化，得到一个新状态new，新状态的能量是。

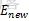假设在状态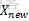时，系统受到某种扰动而使其状态变为。与此相对应，系统的能量也从E(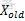)变成E(Xnew)，系统由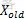状态变为状态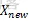的接受概率P

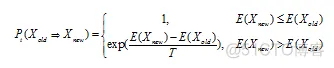
1）若在温度T，当前状态old→ 新状态new

2）若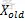E()≤E(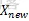)，则接受 new 为当前状态；

否则，若概率

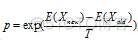
大于[0,1)区间的随机数，则仍接受状态new 为当前状态；若不成立则保留状态 old为当前状态。

重复以上新状态的产生过程。在大量迁移（固体状态的变换称为迁移）后，系统趋于能量较低的平衡状态。

由(1.1)式可知，高温下可接受与当前状态能差较大的新状态为重要状态，而在低温下只能接受与当前状态能差较小的新状态为重要状态。这与不同温度下热运动的影响完全一致，在温度趋于零时，就不能接受任何成立

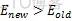
时的新状态new了。上述接受新状态的准则称为Metropolis准则，相应的算法被称为Metropolis算法。

6、模拟退火算法的demo

登录后复制

#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <string>
#include <algorithm>
#include <random>
#include <cmath>
using namespace std;
 
#define ITERS 100 //迭代次数
#define T 100
#define T_min 1e-8
#define delta 0.98
#define INF 1e9
 
double x[ITERS];
 
double F(double x)
{
    return 1/4 * pow(x, 4) - 5/3 * pow(x, 3) + 3 * pow(x, 2) + 1;
}
 
void init()
{
    static std::mt19937 rng;
    static std::uniform_real_distribution<double> distribution(-2, 4);
    for (int i = 0; i < ITERS; i++)
    {
        x[i] = distribution(rng);
    }
}
 
double sa()
{
    double ans = INF;
    double t = T;
    while (t > T_min)
    {
        for (int i = 0; i < ITERS; i++)
        {  
            static std::mt19937 rng;
            static std::uniform_real_distribution<double> distribution(0, 1);
            double f_old = F(x[i]);
            double temp_x = x[i] + (distribution(rng) * 2 - 1) * t;
            if (temp_x >= -2 && temp_x <= 4)
            {
                double f_new = F(temp_x);
                if (f_old > f_new)
                    x[i] = temp_x;
                else
                {
                    double p = exp((f_new - f_old) / t);
                    if (p > distribution(rng))
                        x[i] = temp_x;
                }
            }
        }
        t = t * delta;
    }
    for (int i = 0; i < ITERS; i++)
    {
        ans = min(ans, F(x[i]));
    }
    return ans;
}
int main()
{
    init();
    cout << sa() << endl;
    system("pause");
    return 0;
}

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删