疲劳、断裂、耐久等术语经常交叉使用。然而每一个术语传达一个特定的意思。
用MSC手册原话,疲劳是:结构在承受重复性、变化的载荷,此载荷未达到足以使结构断裂的量级,但结构发生断裂的现象。
疲劳同样可以认为是裂纹萌生并生长,或者裂纹从之前存在缺陷增长,直到达到一个严重的尺寸,诸如分离成两部分或更多部分。
疲劳分析通常采用两种理论模型:1)应力-寿命(S-N)法,通常被成为全寿命法,认为裂纹萌生与裂纹生长没有差别;2)局部应变或应变-寿命(e-N)法,通常被成为裂纹萌生法,该方法主要关心裂纹萌生。
断裂重点涉及初始裂纹的生长与扩展。MSC Nastran的疲劳分析涉及前面两种疲劳分析方法,不适用于裂纹的生长与扩展。对此,可以参考MSC Nastran的cohesive zone模块或虚拟裂纹张合技术(VCCT)或MSC Fatigue,他们使用LEFM方法针对裂纹增长的预测。
耐久是影响产品寿命多方面因素的总称呼,不仅涉及疲劳、断裂,同样涉及载荷状态、环境因素、材料特性、测试仿真等等。产品实际的耐久性项目需要多方面因素的考虑。
所有的疲劳都是动态诱发的。也就是说疲劳,必须有一些足以导致疲劳破坏发生的动力学载荷。现实中没有物体是真正静止的。一些动力学载荷是很难被发现的,改变地很慢,重复的,而其他类型的载荷是相当显著地、本质是随机的,比如发动机噪声。针对以前载荷类型的分析技术适用于时域的疲劳技术。后来被描述成随机,因为他们不是重复的。
传统的随时间变化的振动载荷定义的疲劳分析技术已经被广泛使用。有时候这些时间历程变得非常复杂、费时、本质是随机的,导致常用的瞬态FEA分析和准静态疲劳分析非常耗时、冗长。动力学分析专家已经使用频域技术去理解承受这种类型载荷结构的响应,主要是没有必要去耗费计算时间,同时可以减少硬盘存储空间,但同样可以理解动力学特性。
绝大部分工程师,如果被问定义一个随机载荷输入或结构的输出响应,都将定义像下面的随机时间历程。这个过程可以被描述成随机的和时域的。
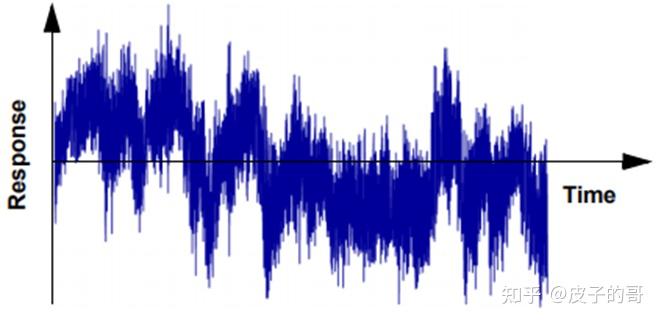
时域随机信号
随机信号是可以被统计的,傅里叶分析允许任何随机载荷的有限长度的历程被替代成一组正弦波函数,每一个正弦函数具有独有的值(幅值、频率、相位)。这个替代被称为确定性的,因为每一个单独的正弦波在任一时刻被精确描述。它仍然是基于时间的,因此用时域定义。
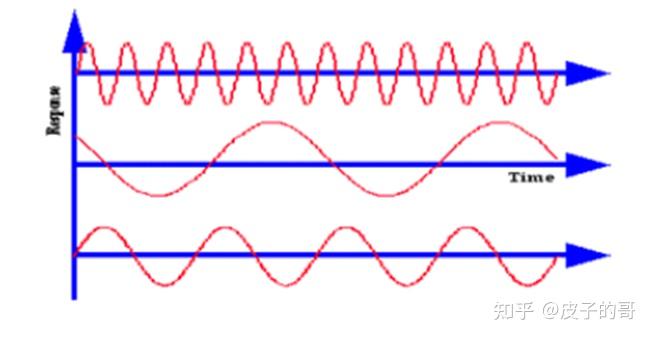
多组正弦波叠加来表示随机信号
作为傅里叶分析的扩展,傅里叶变换允许任何过程被比如PSD的谱函数替代。该谱函数是一个频率相关的函数,因此被称为在频域中。它让然是一个函数的随机定义。
在时域,输入是载荷时间历程的形式(比如风速)。结构模型可以通过FEA替代。模型的输出也表达为时间历程,在此过程中,在结构中某一位置的应力随时间变化。
在频域,输入是给定的PSD形式,以风速来说,结构通过线性传递函数将风速输入关联为结构特定位置的输出应力的形式来构建。模型的输出形式被表达为PSD形式。
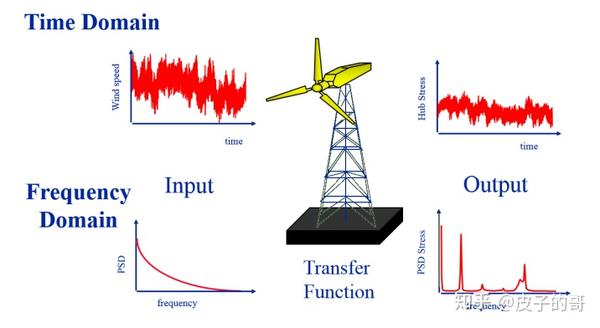
从输入载荷到输出响应的传递函数的描述
时间历程可以在时域与频域之间通过傅里叶变换或逆傅里叶变换被转换。用这种方法,工程师可以同时看到一个信号的时域和频域表达。
FFT是一组关于频率的复数。正弦波的圆频率ω、幅值A、初始相位角φ,用频域形式,以沿着频率轴发生在ω处的尖峰来表达。如果FFT的幅值谱被绘制,这个尖峰下的面积代表该正弦波的幅值A。当FFT的相位谱被绘制,这个尖峰下的面积代表该正弦波的初始相位角。
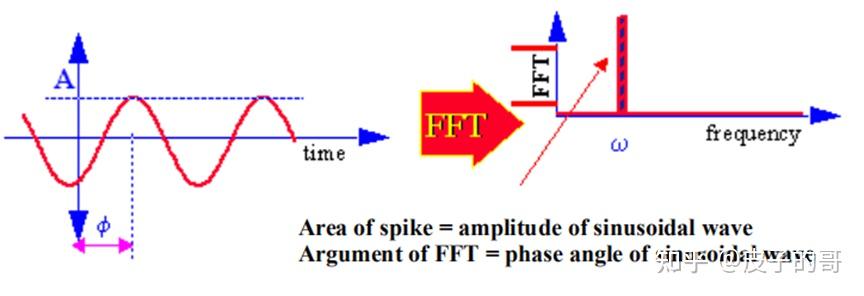
频域中正弦波的描述
法国数学家傅里叶假定任何周期函数可以被表达为,一系列不同频率、幅值和相位的正弦波的组合。每一个单独的正弦波可以被表达为频域下的尖峰,随着正弦波数量的增多,相邻频率差趋于0,尖峰趋于合并成连续函数。因此,如果我们想找到在特定频率范围内的正弦波的幅值和相位,比方说,介于2到2.5Hz,我们可以测量曲线在该频率范围内的面积,这个面积被给成复数的形式,幅值可以通过它的模获得,相位可以通过它的幅角获得。
对很多工程案例,我们仅仅关心不同正弦波的幅值,而不关心它的初始相位。实际上,在很多情况下,初始相位角总是随机的,因此这证明没有必要展示它。
PSD(功率谱密度)函数可以通过提取FTT模的平方有效获得。
频域技术最早与1940s被开发。该方法被用于调查电子线路噪声的起因。随着功率这个参数被测量,它被发现进入谱的方法。正弦波幅值的均方被使用,它被早期模拟电路使用。
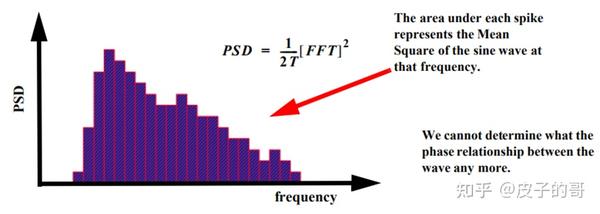
功率谱密度函数
PSD包含正弦波的频率成分、幅值成分,但没有相位关系。为了从PSD中重新生成时间历程,在应用逆傅里叶变换之前,我们必须重新引入随机信号的相位角。再生时间历程信号不在和原来的一样,但在统计学上是等效的。
一个正弦时间历程在PSD图上表现为一个尖峰。这个尖峰集中在正弦波频率处,尖峰面积代表此波幅值的均方。理论上这个尖峰应该是无限高、无限窄的正弦波。然而,由于数值分析,这个尖峰具备有限高和有限宽。
窄带过程,是仅仅由在窄带频率范围的正弦波组成的。
宽带过程,是由在宽带频率范围的正弦波组成的。在PSD绘制中所示,既有一系列的分离尖峰,也覆盖宽的频率范围。
白噪声是一种特殊的时间历程,它是由覆盖整个频率带的正弦波组成,在PSD绘制上,表现为平直线。
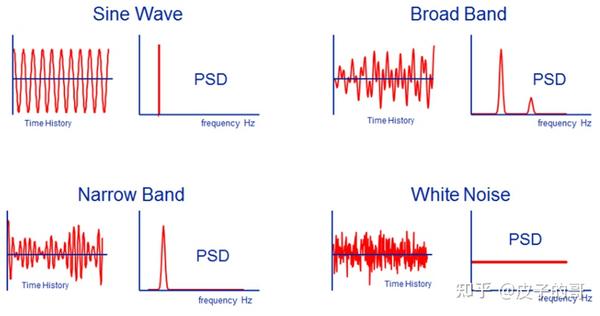
时域信号描述VS PSD描述
本节部分用到的信号参数用于NEVF疲劳求解过程。
参数γ被称为不均衡系数,由γ=E[0]/E[P]确定,E[0]代表向上的均值交叉点(当均值为0,成为向上0点交叉点)的数量,E[P]代表峰值的数量。它意味着,对于一个正弦波每一个峰值出现的平均向上零点数量。
随机应力或应变时间历程可以用统计参数来正确的描述。那是因为任何样本的时间历程仅可以被当作随机发生的无限数量样本中的一个。每一个时间样本是不同的。然而,只要样本足够长,每个样本的统计数据将是常数。
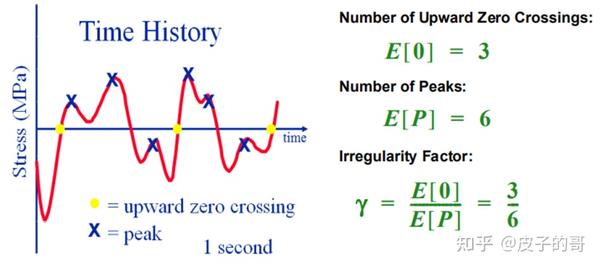
时域中的信号参数
在信号中,两个最重要的统计参数是零点交叉和峰值。以上图中显示的是从一个典型宽带信号截取的一秒片段。E[0]代表向上的均值交叉点数量。E[P]代表峰值的数量。
既然我们关注频域的结构分析,我们需要一种从应力PSD直接获取应力雨流范围的概率密度函数(PDF)的截取方法。换言之,我们需要雨流循环数量,正像我们从时间信号中获得的一样;在此,雨流范围的PDF(雨流循环数量的统计表达)替代雨流循环数量。
从一个PSD获得的特征信息是PSD函数的 n阶矩。相关的谱矩如下:
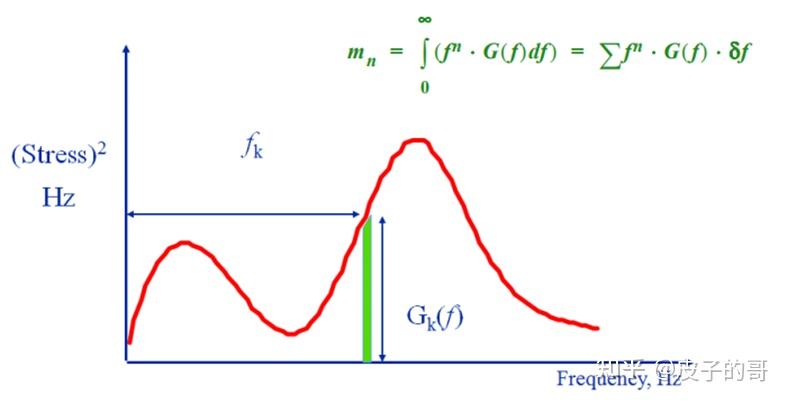
PSD中矩的计算
理论上,为了完整展示原来进程的特征,所有可能的矩需要被计算。然而,实际中,发现m0、m1、m2、和m4对于随后的疲劳分析计算已经足够了。
首次利用PSD提供评估疲劳破坏的工作是 S.O. Rice 于1954年完成的,他提出了利用谱矩 m_{n}m_{n} 在随机信号中表达每秒向上的均值交叉点数量、每秒峰值数非常重要的关系。
利用上面提到的方法,不均衡系数γ被评估。
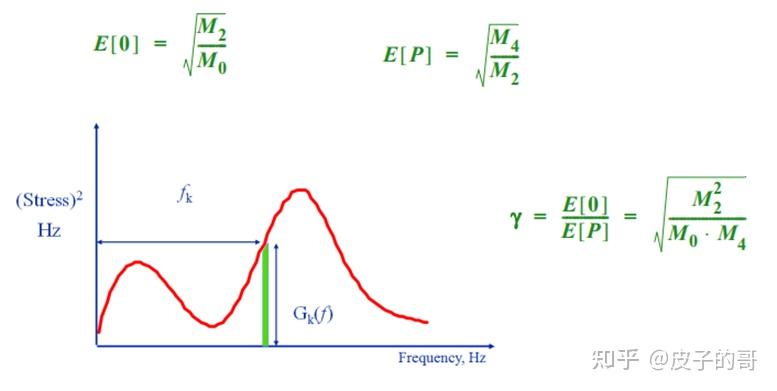
PSD中的信号参数
从应力时间历程或应变时间历程中,两个重要的概率密度函数被计算,他们是幅值和峰值的PDF。对于绝大部分工程目的,幅值PDF、峰值PDF大致符合正态分布;除了窄带过程,峰值PDF大致等效为瑞利PDF。
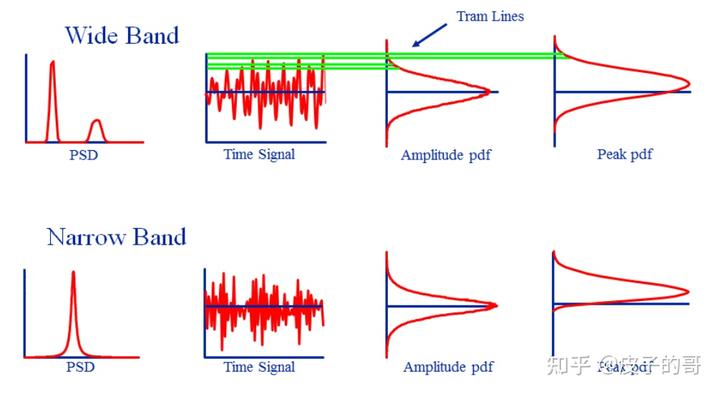
峰值PDF与幅值PDF
在时域中,结构模型可以用FE代替,用瞬态响应分析。这个模型的输出是时间相关的应力、应变或结构在特定位置的位移。对于这种分析类型,获得每一个时间步的载荷历程,需要考虑之前的载荷步。这意味着,两个时间历程的响应的计算时间是一次时间历程响应的两倍。
在频域,结构通过一个线性传递函数关联的加速度(也可能是结构应力、应变或位移)输入载荷构建。模型输出被表达为响应的PSD。在频域,线性传递函数仅需要被计算一次,因此两此载荷工况需要的时间仅比一次工况多一点,其他额外工况也会很快计算完成。
如果线性结构承受一个正弦变化的载荷力,结构将随着载荷力响应为相同频率下的正弦位移。对于线性结构,我们可以预计载荷力的变化会造成结构位移的线性变化。
结构位移峰值随着载荷频率变化,所以响应参数与频率相关。传递函数(TF)被一系列与频率相关的响应参数组成的。因此,我们可以使用传递函数(TF),通过峰值载荷F乘以传递函数去预测结构位移峰值。
传递函数(TF)同样可以用于频域。例如,我们用载荷的峰值谱乘以传递函数,结果将得到位移的峰值谱。
传递函数(TF)可以用于一系列计算方法,包括FEA分析、从测试数据得到数据。一个易于理解的计算TF的方法是,多试验设备或FEA模型施加一系列正弦波,然后找到结构在每个频率下的响应峰值。结构响应不是必须以位移的形式,它可以以线性应变或应力的形式。
为了随后PSD分析得到正确的单位,响应参数需要被平方。这是因为PSD的单位是目标的平方每Hz。以海岸平台为例,输入载荷通常是海洋状态谱。PSD定义的是海洋平面高度特性。在时域,海平面高度随时间变化。因此输入PSD单位可以是m2/Hz。
任何疲劳分析的开始都是对结构响应的计算,该响应通常被表达成时域下的应力或应变历程。针对损伤统计的Palgren-Miner理论被广泛使用。该理论线性假定:由部分应力范围计算的损伤,可以合计入总的损伤,且与其他峰值造成的损伤相互独立。每一个应力范围的比例(损伤比)被计算,该比例等于在特定应力范围的循环圈数n,除以在这个应力范围失效前允许的最大圈数N(由S-N曲线获得)。当所有应力范围的比例之和等于1,假定失效发生。
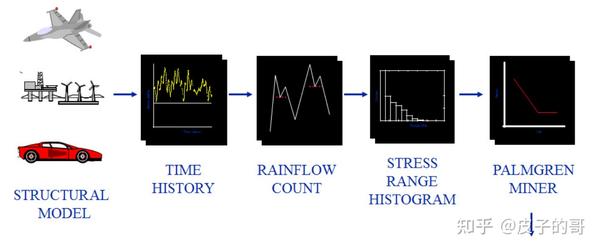
时域疲劳寿命评估过程
上图中涉及雨流计数与S-N数据的内容,在此略过,网上已有大量资料介绍。
随机响应历程的损伤
一旦应力范围直方图被转化为应力范围概率密度,然后由一个简洁有效的方程去描述,承受这种载荷历程下的疲劳损伤的预测。概率密度函数(P(S)),代表载荷的特性。为了计算结构寿命周期的疲劳损伤,材料的S-N数据必须通过参数k和m定义;另外,循环总数的时间必须从单位时间的峰值数得到,即E[P]。如果在时间T内的损伤大于1,然后结构被认为已经失效。或者疲劳寿命可以通过将总时间设置为1,然后从方程中找到以秒为单位的疲劳寿命。

随机响应历程中的损伤
该章节部分描述了从应力PSD中计算疲劳寿命、损伤的多种方法。这些技术分为两大类:a、直接评估疲劳寿命;b、间接利用计算雨流循环的PDF来估算疲劳寿命。更多相关工作已经于最近30多年产生,这些技术已经嵌入MSC Nastran软件算法中。
通用的疲劳损伤方程
这个方程和上面展示的是一样的,表示在时域和频域方法的等效。
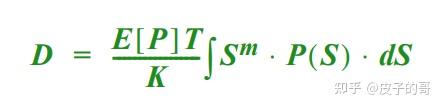
疲劳损伤方程
频域VS时域模型
下面,第一幅图片显示了在时域中疲劳寿命评估的全部过程,第二幅图片显示在频域中的方法。如果我们假定显示的结构模型是FEA模型,这个模型在时域和频域计算方法中是一样的。
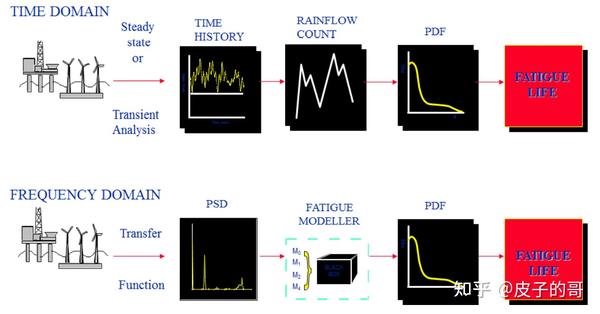
频域VS时域的针对疲劳寿命评估方法
为了得到应力或应变响应的时间历程,需要进行稳态分析或瞬态分析。对于随机响应历程,显而易见是一个瞬态分析。疲劳分析是一个时域的,如早期描述的一样。在频域,结构模型的传递函数首先被计算,传递函数TF完全依赖输入载荷以及系统/模型的固有属性。任何输入载荷的PSD造成的PSD响应,通过TF乘以输入载荷PSD获得。
窄带求解技术
S. Bendat (1964) 开发了这项技术,因此也叫Narrow Band solution。这个技术的定义仅用到谱矩 m0。然而,事实上求解技术仅适合特定类型的响应条件,对于实际工程人员帮助不大。
这是首次从PSD预测疲劳损伤的频域方法,它假定应力峰值的PDF与应力幅值的PDF相等。窄带求解技术是通过利用应力范围的PDF代替峰值Rayleigh PDF来实现。
这种求解技术的问题在于:通过使用Rayleigh PDF,正波谷与负波峰被忽略,所有正波峰与相应的近似量值的波谷相同,尽管不论它们是否可以组成应力循环。对于宽带响应数据,这种方法高估了大应力范围的概率,所以损伤计算趋于保守的。
Dirlik 求解技术
所有现存的频域疲劳分析技术假定雨流范围的PDF是控制疲劳寿命的因素。因此,一个更好的方法是,直接从PSD中评估,而不是使用Narrow Band solution作为开始点。Dirlik提出一个经验:雨流范围的PDF的解析解,可以利用蒙特卡洛技术,通过计算机仿真来构建。尽管看上去比其他方法复杂,该函数仅由m0、m1、m2和m4构成。该方程已经广泛应用于解决问题,胜过其他的方法。

Dirlik求解方法
Steinberg 求解技术
Steinberg 方法带来一种非常简单的求解技术,基于这样的假设:没有应力循环发生在大于6*RMS。应力范围的分布被定义为一个高斯分布。它定义应力范围循环按照如下概率发生。

Steinberg 求解方法
在随后的疲劳分析中,可能要定义最大应力范围。如果定位为6 * RMS,使用这种方法,大应力范围被忽略;若不理会,MSC Nastran会自动设置该值为9*RMS。任何低于此值,可能导致疲劳损伤的偏低预测。
MSC Nastran疲劳损伤计算采用Dirlik(默认)、Narrow Band、Steinberg技术。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删