1、Minitab 中包括哪些随机数据和概率分布功能
生成随机数据根据一列数据或从选定的数据分布创建一个或多个随机数据列。在 Minitab 中,选择计算 > 随机数据。
- 要根据工作表中的数据创建随机样本,请选择来自列的样本。
- 要根据某特定分布创建随机样本,请指定该分布和相应参数。
指定随机数字生成器为随机数生成器指定一个起点,以便将来生成相同的随机数据集。在 Minitab 中,选择计算 > 设置基数。创建分布的 PDF、CDF 或逆 CDF。计算所选分布的 PDF、CDF 或逆 CDF。在 Minitab 中,选择计算 > 概率分布。
2、访问数据分布的方式
一组数据可按许多不同方式分布或散布。例如,掷骰子所得的数据可以是从 1 到 6 的随机整数值。制造过程所得的数据可以目标值为中心进行分布,也可以包括远离中心值的数据值。
可以通过图形、描述性统计量或者与理论分布的比较来评估数据分布:图形通过图形(如直方图),可以直接深入了解数据集的分布情况。直方图可以帮助您观测:
- 数据聚类是围绕单个值,还是具有多个峰值或模式。
- 数据是稀疏散布于宽广的范围,还是位于较小的范围。
- 数据是偏斜的还是对称的。
描述性统计量用于描述包含数字值的数据的中心趋势(平均值、中位数)和展开(方差、标准差)的描述性统计,这些统计添加了明细层并且可用于与其他数据集进行比较。理论分布最后,一些常见分布可通过正态分布、Weibull 分布和指数分布等进行标识和称呼。例如,正态分布始终为钟形,且沿均值对称分布。真实数据将只能接近于这些完全分布。如果存在紧密拟合,则可认为数据由给定分布进行了合理建模。可使用统计 > 质量工具 > 个体分布标识来确定最适合您数据的分布。
3、连续和离散概率分布
概率分布要么是连续概率分布,要么是离散概率分布,这取决于它们是定义连续变量还是离散变量的概率。
- 什么是连续分布?
连续分布描述连续随机变量的可能值的概率。连续随机变量是具有一组无限且不可计数的可能值(称为范围)的随机变量。
连续随机变量 (X) 的概率被定义为其 PDF 曲线下的面积。因此,只有值范围才能具有非零的概率。连续随机变量等于某个值的概率始终为零。
重量分布示例
连续正态分布可以描述成年男性的体重分布。例如,可以计算男性体重为 160 到 170 磅之间的概率。
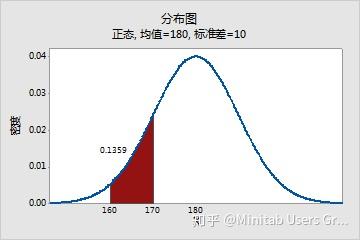
但是,X 精确等于某个值的概率始终为零,因为曲线下单个点的面积为零(没有宽度)。例如,男子体重恰好为 190 磅(至无限精确)的概率为零。您可以计算男性体重超过 190 磅或小于 190 磅的概率,或者介于 189.9 到 190.1 磅之间的概率,但恰好等于 190 磅的概率为零。
什么是离散分布?
离散分布描述离散随机变量的每个值的发生概率。离散随机变量是指具有可计数的值的随机变量,例如非负整数的列表。
在离散概率分布中,离散随机变量的每个可能值可与一个非零概率相关联。因此,离散概率分布通常具有表格形式。
客户投诉数量示例
不同于连续分布,在离散分布中,您可以计算 X 恰好等于某个值的概率。例如,可以使用离散 Poisson 分布来描述一天内的客户投诉数量。假设平均每天的投诉数量为 10,并且您想知道在一天中接收 5、10、15 个客户投诉的概率。
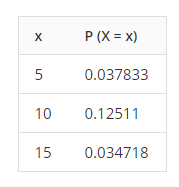
您还可以查看分布图上的离散分布,以了解各范围之间的概率。

4、使用概率密度函数 (PDF)
- 什么是概率密度函数 (PDF)?
概率密度函数可帮助确定随机变量值的较高和较低概率的区域。
离散 PDF 的示例
对于离散变量,PDF 将给出给定 x 值的概率值。例如,糖果制造商生产多种颜色的某一类型糖果。生产的糖果中有 30% 为黄色,10% 为橙色,10% 为红色,20% 为绿色,30% 为蓝色。

连续 PDF 的示例
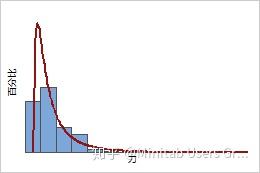
概率密度函数 (PDF) 是一个用于表示连续随机变量的概率分布的等式。例如,为葡萄酒瓶切割软木塞的机器可产生直径不同的软木塞。在下面的软木塞直径条形图中,每个条形表示具有相应直径的软木塞的百分比。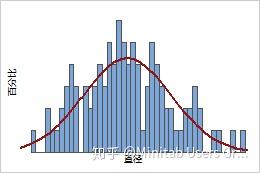
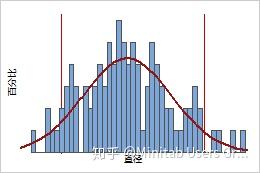
广为熟知的钟形曲线表示正态分布的 PDF。尽管软木塞直径服从正态分布,但其他测量值(如将软木塞从酒瓶中拔出所需的力)可能服从其他分布。例如,对数正态分布的 PDF 有一个长的右尾。例如,对数正态分布的 PDF 有一个长的右尾。
5、使用累积分布函数 (CDF)
- 什么是累积分布函数 (CDF)?
累积分布函数 (CDF) 计算给定 x 值的累积概率。可使用 CDF 确定取自总体的随机观测值将小于或等于特定值的概率。还可以使用此信息来确定观测值将大于特定值或介于两个值之间的概率。
使用 CDF 评估填充重量的示例
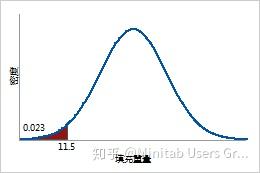
例如,罐装苏打水的填充重量服从正态分布,且均值为 12 盎司,标准差为 0.25 盎司。概率密度函数 (PDF) 描述了填充重量的可能值的可能性。CDF 提供每个 x 值的累积概率。

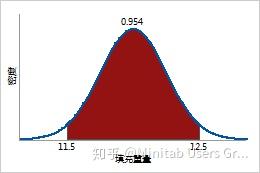
使用 CDF 可以确定随机选择的罐装苏打水的填充重量小于 11.5 盎司、大于 12.5 盎司或介于 11.5 到 12.5 盎司之间的概率。

使用 CDF 计算 p 值
为了计算 F 检验所对应的 p 值,必须首先计算累积分布函数 (CDF)。p 值为 1 – CDF。
假设您使用下列自由度执行一个多元线性回归分析:DF(回归)= 3;DF(误差)= 25;F 统计量 = 2.44。
计算 F 检验的 p 值
- 选择计算 > 概率分布 > F。
- 选择累积概率。
- 在非中心参数中,输入 0。
- 在分子自由度中,输入 3。
- 在分母自由度中,输入 25。
- 选择输入常量,并输入 2.44。
- 在可选存储中,输入 K1。单击确定。 K1 包含累积分布函数。
使用“计算器”从 1 减去 p 值
- 选择计算 > 计算器。
- 在将结果存储在变量中中,输入 P 值。
- 在表达式中,输入 1-K1。单击确定。
计算的 p 值为 0.08795。使用 0.05 的截止值,您不能断定统计显著性,因为 0.08795 不小于 0.05。注意
该示例适用于 F 分布;但是可针对其他分布使用类似的方法。
6、使用逆累积分布函数 (ICDF)
- 什么是逆累积分布函数 (ICDF)?
逆累积分布函数给出与特定累积概率关联的值。可使用逆 CDF 确定与特定概率相关联的变量值。 - 使用 ICDF 确定保修期的示例
例如,一家电器制造商要调查其烤箱内加热管的失效时间。他们想要确定特定百分比的加热管失效的时间,以便设定保修期限。加热管的失效时间服从正态分布,其均值为 1000 小时,标准差为 300 小时。概率密度函数 (PDF) 可帮助确定较高和较低失效概率的范围。逆累积分布函数给出每个累积概率的对应失效时间。
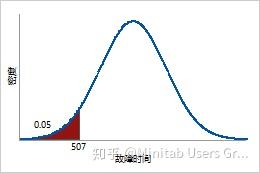
使用逆累积分布函数估计 5% 的加热管失效所需的时间,95% 的加热管开始失效以及全部失效所需的时间,或仅剩 5% 加热管未失效的时间。特定累积概率的逆累积分布函数等于概率密度函数曲线下阴影区域右侧的失效时间。
确定 5% 的加热管失效所需的时间
- 选择计算 > 概率分布 > 正态。
- 选择逆累积概率。在均值中,输入 1000。在标准差中,输入 300。在输入常量中,输入 0.05。
- 单击确定。
5% 的加热管失效所需的时间预计为 0.05 倍的逆累积分布函数或 506.544 小时。
确定 95% 的加热管失效所需的时间
- 选择计算 > 概率分布 > 正态。
- 选择逆累积概率。在均值中,输入 1000。在标准差中,输入 300。在输入常量中,输入 0.025。单击确定。2.5% 的加热管失效所需的时间预计为 0.025 倍的逆累积分布函数或 412 小时。
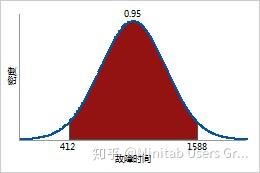
- 重复步骤 2,但输入 0.975 而非 0.025。单击确定。97.5% 的加热管失效所需的时间预计为 0.975 倍的逆累积分布函数或 1588 小时。
因此,95% 的加热管开始失效和全部失效所需的时间预计分别为 0.025 倍和 0.975 倍的逆累积分布函数或 412 小时和 1588 小时。
确定 5% 的加热管未失效的时间
- 选择计算 > 概率分布 > 正态。
- 选择逆累积概率。在均值中,输入 1000。在标准差中,输入 300。在输入常量中,输入 0.95。
- 单击确定。
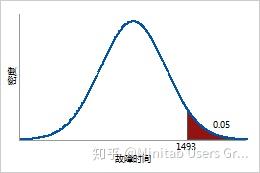
仅剩 5% 的加热管未失效的时间预计为 .95 倍的逆累积分布函数或 1493 小时。
- 将 CDF 和 ICDF 与超几何分布结合使用的示例
在尝试确定离散分布的逆累积概率时,输出结果中将包含两组列。
假设某个比率的逆累积概率为 p。输出内容中第一组列将列出最大的 x,使 P(X ≤ x) ≤ p。第二组列将列出最小的 x,使 P(X ≤ x) ≥ p。
计算超几何分布的累积概率
- 在工作表的 C1 列中,输入 0 1 2。
- 选择计算 > 概率分布 > 超几何。
- 选择累积概率。
- 在总体大小 (N)中,键入 20000。
- 在总体中的事件计数 (M)中,键入 2000。
- 在样本数量 (n)中,键入 20。
- 选择输入列并输入 C1。单击确定。
将出现此输出:

可以按如下方式解释输出内容:
- P(X ≤ 0) = 0.121448。获得 0 个缺陷的概率大约为 12%。
- P(X ≤ 1) = 0.391619。获得 0 或 1 个缺陷的概率大约为 39%。
- P(X ≤ 2) = 0.676941。获得 0、1 或 2 个缺陷的概率大约为 68%。
计算超几何分布的逆累积概率
现在,您知道了与缺陷数相关联的累积概率,可以计算逆累积概率了。
假设您要计算缺陷数 x,使累积概率 p 为 0.50。通过前面的结果了解到,P(X ≤ 1 ) = 0.391619 并且 P(X ≤ 2 ) = 0.676941。由于超几何分布是一种离散分布,缺陷数无法介于 1 和 2 之间。换言之,可以有 1 个或 2 个缺陷,但不会有 1.4 个缺陷。因此,如果选择输入常量并输入 0.50,则 Minitab 将会在输出中计算这两个概率,如以下示例所示:
- 选择计算 > 概率分布 > 超几何。
- 选择逆累积概率。
- 在总体大小 (N)中,键入 20000。
- 在总体中的事件计数 (M)中,键入 2000。
- 在样本数量 (n)中,键入 20。
- 选择输入常量,并键入 0.50。单击确定。
将出现此输出:

第一个概率指示 x 的值,使 P(X ≤ x) < p;第二个概率指示最小的 x,使 P(X ≤ x) ≥ p。在该示例中,第一个概率显示最大缺陷数 x = 2,使 P(X ≤ 2) < 0.5;第二个概率显示最小缺陷数 x = 3,使 P(X ≤ 3) ≥ 0.5。
- 使用 ICDF 计算临界值
可以使用 Minitab 计算一个假设检验的临界值,而不用在表格中查找该值。
假设您在 α = 0.02、自由度等于 12 的情况下执行卡方检验。对应的临界值是多少?α = 0.02 所对应累积概率值为 1 – 0.02 = 0.98。
- 选择计算 > 概率分布 > 卡方。
- 选择逆累积概率。
- 在自由度中,输入 12。
- 选择输入常量并输入 0.98。
- 单击确定。
Minitab 显示临界值 24.054。对于卡方检验,如果检验统计量大于临界值,则可以断定存在否定原假设的统计学证据。
注意
此示例使用卡方分布。但是,您可以为所选择的任何分布执行相同的步骤。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删
















