Minitab基础描述统计实例分析

数据实例数据简要介绍：

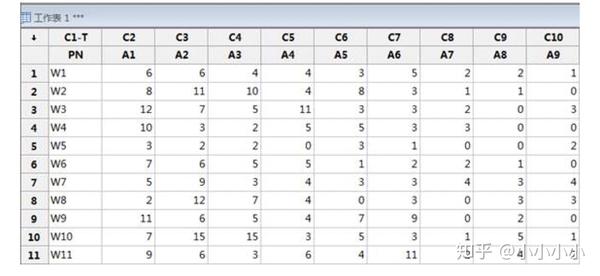
本文共选取了A1—A9共计9种原材料，并捞取其从第一周至第五十周的周用量数据进行分析，目的在于寻找发现使用量的规律，为提前安排相关原材料的备货提供数据支持，数据信息详见下表（由于数据量大，文中W11之后数据暂时隐藏）。

实例分析：

1）基本描述统计量：我们将利用Minitab来计算这些数据的基本描述统计量，并利用基本描述统计量的值来对数据进行简要分析。点击菜单栏“统计”—“基本统计”—“显示描述性统计量”。

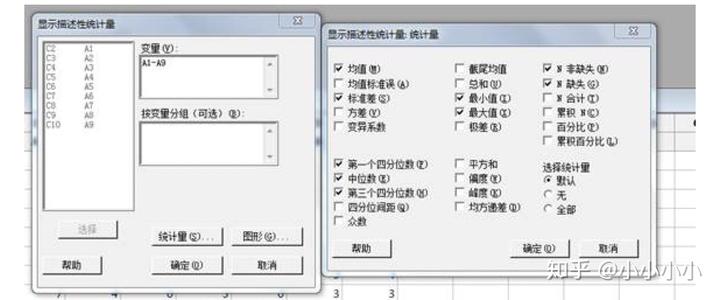
出现上图后将A1—A9选入变量Y列，点击“统计量”后出现右图，将你需要的统计量前打勾，点击“确定”，Minitab就帮我们把各种基本描述统计量都计算出来啦。

2）箱线图：为了更加直观的观察数据，我们选取箱线图来观察数据，在Minitab中点击“图形”—“箱线图”后出现下面窗口，根据数据选择相应的箱线图，由于本文中有多个Y，且不分组，故选取多个Y值简单箱线图。

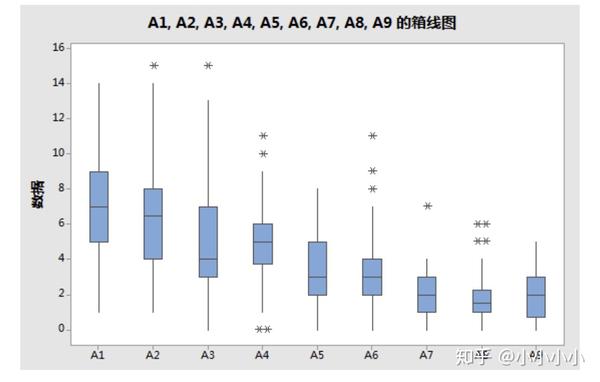
Minitab运行后的箱线图见下，我们根据箱线图能够大致了解数据的分布情况，且软件已自动帮助识别出异常值，星号值即为异常值，需要我们去单独分析异常值的原因，并选择是留下还是删除异常值。

3）标准分

标准分就是标准化的值，表示各个样本距离平均值有多少个标准差，Minitab也可以帮助我们直接将数据标准化，计算出标准分。

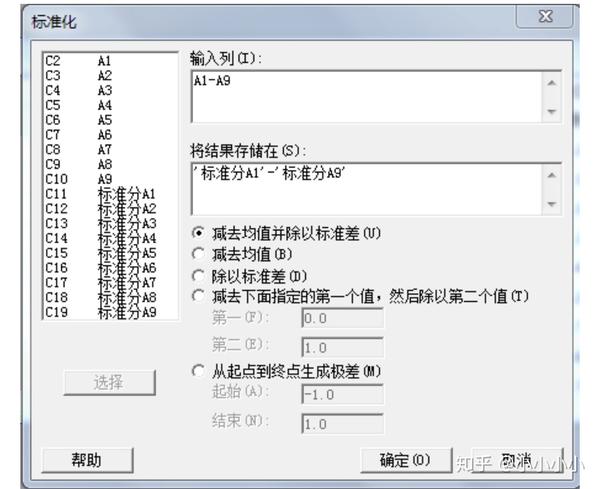
点击“计算”—“标准化”出现上图窗口后，将A1-A9的用量数据作为列，并将结果存储在后面的标准分列里，选择计算方式为减去均值并除以标准差，点击确定后Minitab就为我们自动计算出标准化的值啦。

4）举例分析：以A1，A9两个物料来进行举例分析。

均值：A1平均周用量7.060，A9周用量1.760，A1用量更多。

众数：A1的历史用量中出现最多次的是7，出现过11次；A9的历史用量中出现最多次的是0和1，共计出现了12次。也说明了A1的使用更加频繁。

四分位数：A1四分位数之间的距离较大，A9四分位数之间的距离较小，从箱线图的长短也可以看出A9的用量更加集中，变化范围比A1要小的多。

标准差：A1标准差为3.053，变异系数43.25，A9标准差为1.437，变异系数81.62；标准差和变异系数都反应了数据的变动（离散）程度，两者的区别在于标准差只能观察均值相同的两类数据的变动程度，而变异系数则消除了数据的绝对大小对变动程度的影响，可以观察度量单位或均值不同的两类数据的变动程度。这个案例的数据非常典型，虽然从标准差上看A1的值更高一些，但是消除了数据的绝对大小对变动程度的影响后我们可以看到其实A9的变动程度更大一些，也就是相对来说A9的用量更加不稳定。

根据对这些数据的分析，我们可以将9种原材料的稳定性排序，对不稳定性较大的原材料给予更多的关注，根据均值及变动程度选择合适的安全库存值以避免需求变动带来的缺料等情况的发生。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删