Minitab基础统计操作全掌握

前言：公司使用新制程的IC 工程批。会对CP的DC数据进行大量收集，来分析制程稳定性，排除设计缺陷，确定芯片测试的可靠性。数据处理成为很重要的一步。怎么样可以把测试数据直观的输出给RD。minitab 应该算的上是一个趁手的兵器。当然，大部分的分析和统计在Excel 中也同样可以实现，这个看个人喜好。

1-0基本统计量操作

a,整理好和CP 测试log中 烧录后IC VDD_DRV电压值。输入进minitab 工作表中。

b,minitab 选则:统计->基本统计量->显示描述性统计量。VDD_DRV的基本的统计量结果就会输出在会话中。

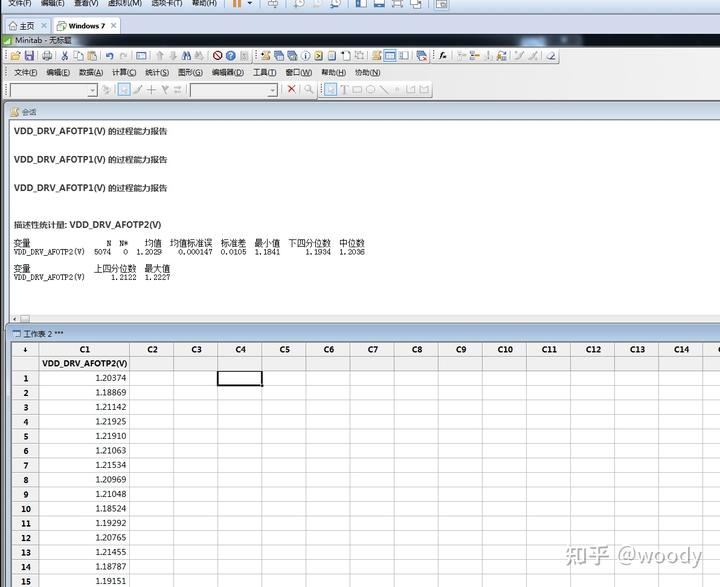
   图1-0 minitab 界面
 

1-1基本统计量说明

N 和 N*： 提供有关数据集中观测值个数的信息：N 是非缺失值的数量。 N* 是缺失值的数量。如果没有缺失值，则不显示此统计量。N=5074颗IC VDD_DRV数据。 N*=0无缺失值。

均值：（也称为平均数）是对分布中心所在位置的度量。只需用所有观测值的和除以观测值个数。极端值会对均值产生极大的影响。 VDD_DRV 均值=1.2029V。（IC TRIM的VDD_DRV 目标值是1.204V）。

\mu=\frac{a_{1}+a_{2}+a_{3}+...a_{n}}{n}\mu=\frac{a_{1}+a_{2}+a_{3}+...a_{n}}{n}

中位数：（也称为第 2 个四分位数或第 50 个百分位数）是数据集中的中点：有一半观测值位于其上，一半观测值位于其下。它通过对数据排序并找出观测值编号 [N + 1] / 2 来确定。如果有偶数个观测值，中位数表示为观测值编号 N / 2 和 [N / 2] + 1 之间的值。 中位数不像均值那样对极端值敏感。因此，当数据包含异常值或偏斜时，通常使用中位数而非均值。

标准差 (StDev)： 度量样本中的观测值偏离均值的程度。它类似于到均值的平均距离（与方向无关）。标准差是最常报告的离差的量度。在样本取自的更广泛总体中，标准差也用作离差的估计值。与均值相似，标准差对极端值也很敏感。如果数据呈正态分布，则标准差和均值可用来确定观测值处于给定值范围内的比例。例如，正态分布中 95% 的值处于均值的 ±1.96 标准差之内。

\sigma=\sqrt{\frac{\sum_{i=1}^{n}（{x_{i} -\mu}）^2}{n}} \sigma=\sqrt{\frac{\sum_{i=1}^{n}（{x_{i} -\mu}）^2}{n}}

均值的标准误 (SE Mean) ：通常不用作描述性统计，但它在假设检验中非常重要。如果您继续从总体中提取相同数量的样本，则均值的标准误是您要从样本均值的分布中观测的离差的估计值。

均值的标准误为标准差除以  \sqrt{N}\sqrt{N} 。

最小值和最大值：评估数据中离差的最简单的方法之一是比较最小值和最大值。最小值是数据集中最小的值，最大值是数据集中最大的值。 最小值和最大值用于计算极差，极差是常用于描述数据集中离差的一个统计量。极差就是最大值 - 最小值。请注意，极差对于极端值非常敏感。

下四分位数：刚好有 25% 的数据小于下四分位数（Q1，也称为第 25 个百分位数）。它等于位置 (N + 1) / 4 的数据值。如果此位置编号不是整数，Minitab 将在该位置两侧的两个观测值之间进行推断。

上四分位数：刚好有 75% 的数据小于上四分位数（Q3，也称为第 75 个百分位数）。它等于位置 3(N + 1) / 4 的数据值。如果此位置编号不是整数，Minitab 将在该位置两侧的两个观测值之间进行推断。 Q1 和 Q3 通常用于计算四分位数极差(IQR)，四分位数极差是用于描述离差的另一个统计量。IQR 是中间 50% 的值的极差，计算公式为 Q3 - Q1。相对而言，IQR 对极端值不敏感。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删