ABAQUS中的单元选择

在有限元分析中，为了能够得到较为精确的收敛解，一方面取决于所用模型的误差，另一方面取决于模拟计算的误差。一个好的有限元模型，不仅需要较高的网格质量，还需要拥有合适的单元类型。ABAQUS为用户提供了丰富的单元库，几乎可以模拟实际工程中任意几何形状的有限元模型，在对一个问题进行分析时，可以根据情况选择使用。

如何才能选取出适合于分析的单元类型呢？我认为首先要了解ABAQUS中对于单元的分类，每种单元特定的使用范围，各种单元类型的节点数目、单元形状、插值函数阶次以及单元构造的方式。然后再根据分析类型和具体问题合理选择。

ABAQUS中最常用的单元包括实体(Solid)单元、壳(Shell)单元和梁(Beam)单元。下面就根据自己对于ABAQUS应用实体单元的学习，将这些单元的特点和使用简单总结如下：

实体单元主要包括完全积分、减缩积分、非协调以及杂交这四种常见的单元模式。

（1）完全积分单元：单元具有规则形状（边是直线并且边与边相交成直角）时，

  所用的Gauss积分点的数目足以对单元刚度矩阵中的多项式进行精确积分。

完全积分的线性单元在每一个方向上采用2个积分点；

完全积分的二次单元在每一个方向上采用3个积分点。如图

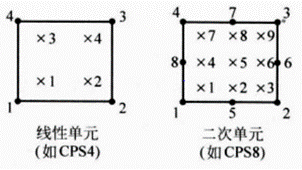
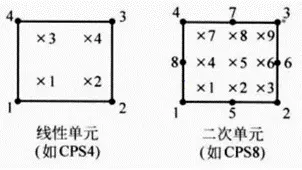
不足：完全积分的线性单元存在“剪切自锁”问题，原因是线性单元的边不能弯曲。在复杂应力状态下，完全积分的二次单元也有可能发生剪切自锁。

（2）减缩积分单元：减缩积分单元比完全积分单元在每个方向上少用一个积分点。

完全积分的线性单元只在单元的中心有一个积分点

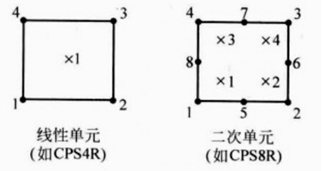
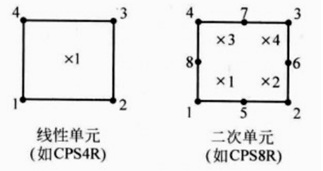
不足：线性减缩积分单元存在“沙漏模式”的数值问题，有可能过于柔软。

ABAQUS通过绘制伪应变能(ALLAE)和内能(ALLIE)来评价沙漏模式对计算结果的影响。

（3）非协调单元：

优点：可以克服完全积分，一阶单元中的剪力自锁问题。

特点：在一阶单元中引入一个增强单元变形梯度的附加自由度。这种对变形梯度的增强允许一阶单元在单元域上对于变形梯度有一个线性变化。

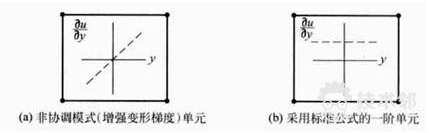
不足：对单元的扭曲很敏感，在使用时必须小心以确保单元扭曲是非常小的。

（4）杂交单元：

应用：当材料行为是不可压缩（泊松比=0.5）或非常接近于不可压缩（泊松比>0.475）时，如橡胶材料，采用杂交单元。

特点：对于具有不可压缩材料性质的任何单元，一个纯位移的... ...

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删