弹性波仿真中纵、横波分离的有效方法探讨

固体中的弹性波含有纵波、横波，也有称为膨胀波、剪切波等等，不同领域叫法不同。
特别是弹性波遇到裂缝、空洞、界面发生散射时，纵波和横波往往会同时产生，如果单单从位移场或应力场是无法区分的
根据弹性波理论，
位移场的散度 就是膨胀波
位移场的旋度就是剪切波
所以对位移场计算一下散度和旋度就可以分别获得膨胀波和剪切波
我只算2D的情况，这里给一个例子（matlab）
dx=0.1e-3;
dy=0.1e-3;
[x,y]=meshgrid(0:x:1e-1,-16e-3:y:-6e-3);
%时间' L3 u; H: u* J$ |: K
t=24e-6;3 A2 m8 M( u+ w% |/ o
%总位移6 {/ q( f9 v& f J+ U5 ]! U
vv=postinterp(fem,'disp_acpn',[x(:';y(:'],'T',t);
vv=reshape(vv,size(x));
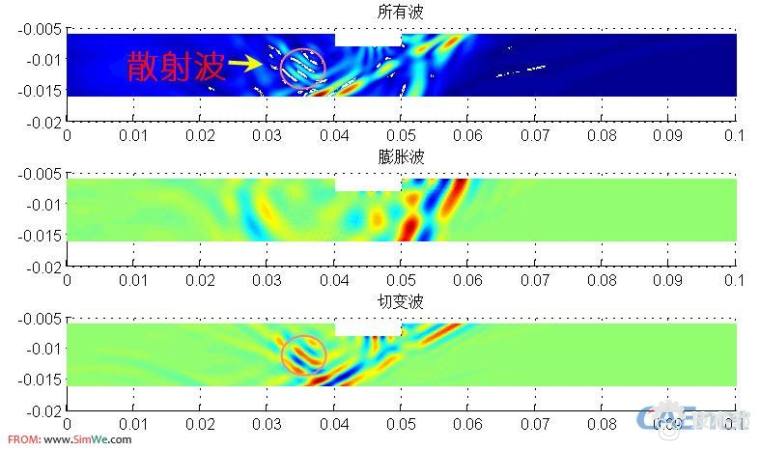
subplot(3,1,1);surf(x,y,vv);axis normal;shading interp;view(0,90);title('所有波')
% return;, T( B/ l9 F: m
%纵波--膨胀波only
ux=postinterp(fem,'ux',[x(:';y(:'],'T',t);
vy=postinterp(fem,'vy',[x(:';y(:'],'T',t);
ux=reshape(ux,size(x));
vy=reshape(vy,size(x));
subplot(3,1,2);surf(x,y,ux+vy);shading interp;view(0,90);title('膨胀波')
%横波--旋变only
uy=postinterp(fem,'uy',[x(:';y(:'],'T',t);
vx=postinterp(fem,'vx',[x(:';y(:'],'T',t);
uy=reshape(uy,size(x));
vx=reshape(vx,size(x));
subplot(3,1,3);surf(x,y,uy-vx);shading interp;view(0,90);title('切变波')
附件中容易看到散射波是剪切波（横波）

纵横波分解2.jpg