
通过以下运动方程来演化带电粒子的运动轨迹:
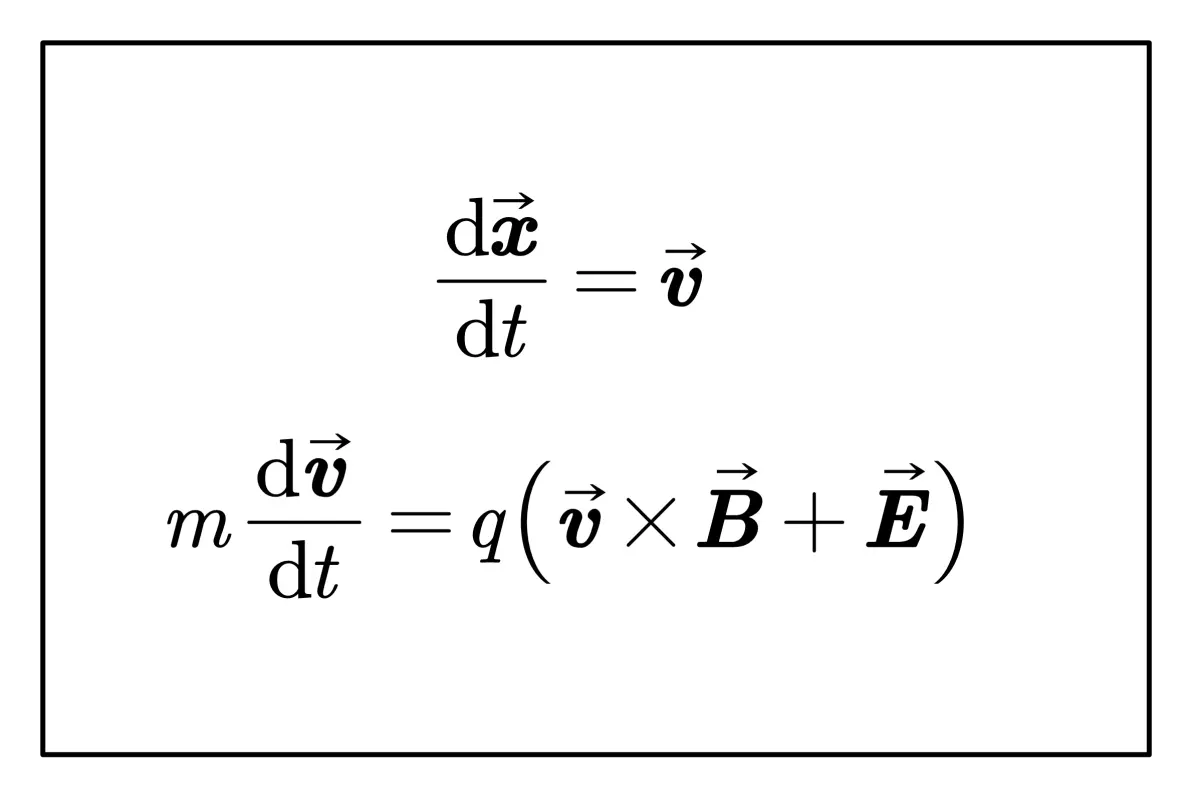
其中 B 为磁场强度, E 为电场强度. 以下是矩阵分量形式:

Boris 算法通过第 i 步相空间坐标求解第 i+1 步相空间坐标 ,上式可写为如下离散格式:
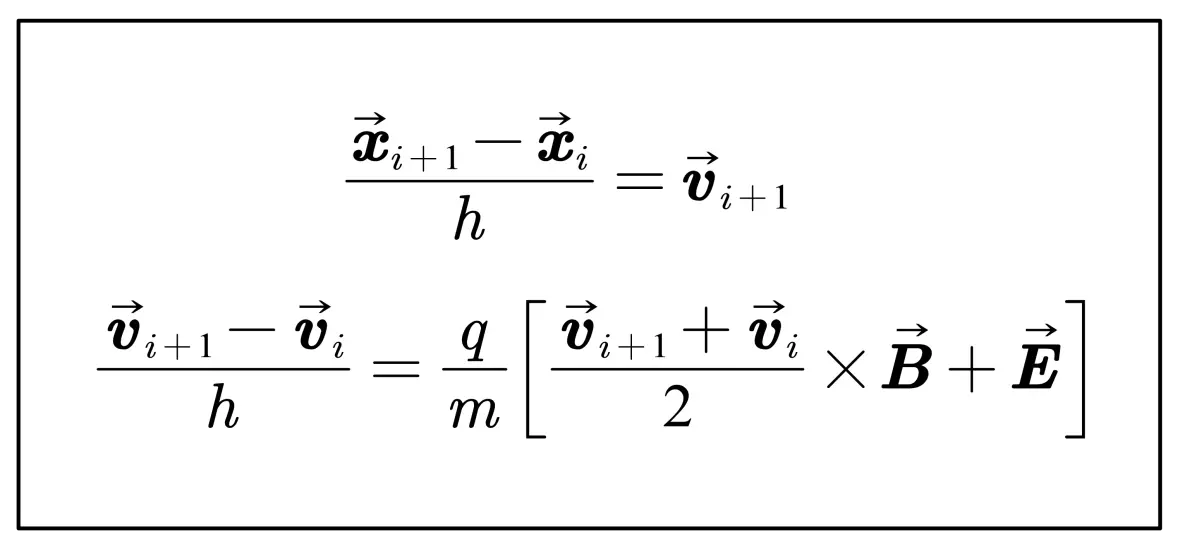
其中 h 为时间步长。线性代数中,Corss操作可以用矩阵相乘表示:

Boris算法的基本思想是将带电粒子的速度分解为两个部分,一个是由电场引起的,一个是由磁场引起的。电场部分可以用欧拉法或其他一阶方法求解,磁场部分可以用一个旋转矩阵来求解。通过将两个部分的速度分别更新,然后再合并,就可以得到粒子的新的速度和位置。离散格式可以改写成如下格式:
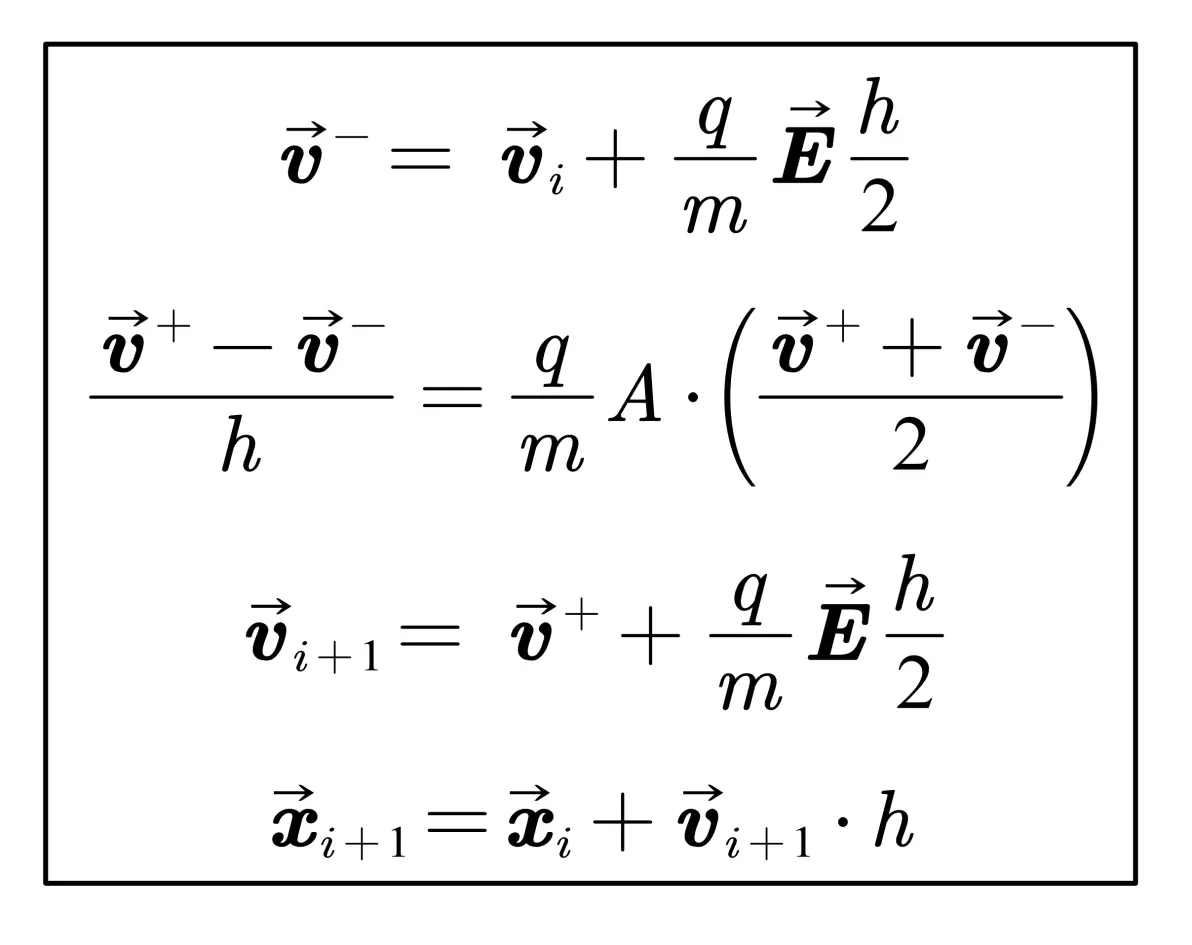
解析计算得到解析式:
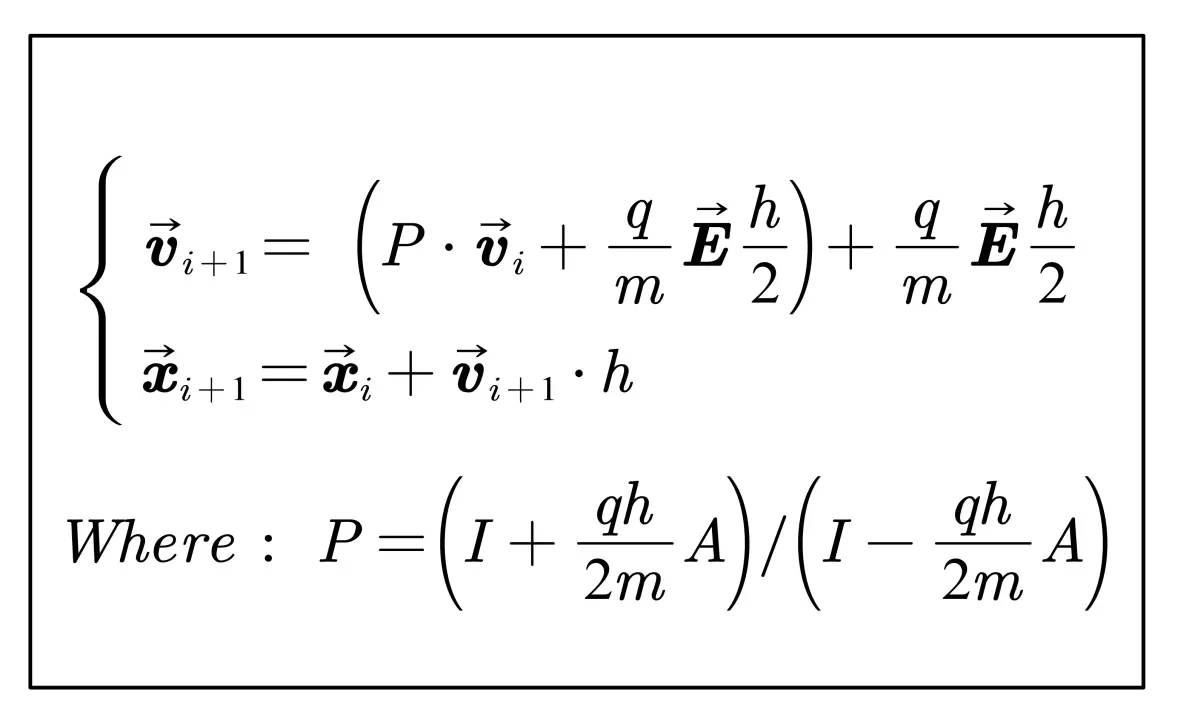
I是对角为1的单位矩阵.第i 步递推到第 i+1步, 电场力驱动的一半首先作用在v_(i)上获得v-, 再通过P矩阵计算得到v+, 进一步将电场力驱动的一半加在上,最终获得v_(i+1).
另外,可以将P矩阵展开,将磁场代入,得到最终迭代解析式:
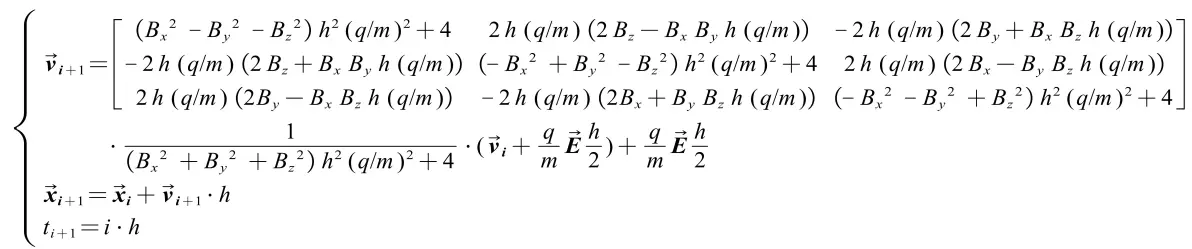
以下是上图的转置:
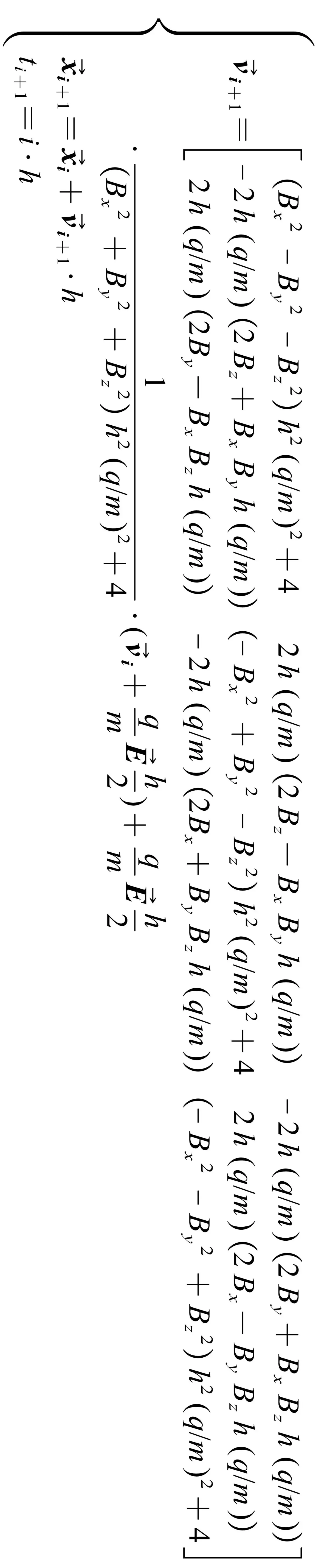

matlab代码 如果你所在的大学是南华大学无论你是毕业设计还是课程设计,都不要抄代码
%% by Qia
% 参数设置
q=1; m=1; g=0;%比荷 重力加速度
E=[ 0 0 0 ]; %Ex=0; Ey=0; Ez=0;
B=[0 0 1 ]; %Bx=0; By=0; Bz=1;
p0=[0 0 0 ] ; %x0=0; y0=0; z0=0; 粒子位置
v0=[1/2 0 1 ]; %vx0=1; vy0=0; vz0=0;
t=10;dt=0.002;
% 绘图设置
figure('name', 'move');
% colordef black;
grid on;
plane = scatter3(p0(1), p0(2), p0(3), 'c', 'o'); % 粒子位置
planev = text(p0(1) + 0.4, p0(2) + 0.4, p0(3) + 0.31, ['v=', '(', num2str(single(v0)), ')']); % 粒子速度
planep = text(p0(1) + 0.4, p0(2) + 0.4, p0(3) + 0.205, ['p=', '(', num2str(single(p0)), ')']); % 粒子位置
planet = text(p0(1) + 0.4, p0(2) + 0.4, p0(3) + 0.4, ['t=', '0']); % 时间
h = animatedline('color', 'b'); % 粒子轨迹
view(3);
xlabel('x');
ylabel('y');
zlabel('z');
hold on;
% 运动方程
for i = 1 : t / dt + 1
B=50*b(p0);%在这里可以设置随位置,时间而改变的磁场、电场等
[v,p]=a2(p0, v0, E, B, dt, q/m);
addpoints(h, p(1), p(2), p(3)); % 添加轨迹点
set(plane, 'Xdata', p(1), 'Ydata', p(2), 'Zdata', p(3)); % 更新粒子位置
planep.String = ['p=', '(', num2str(single(p)), ')']; % 更新粒子位置文本
planev.String = ['v=', '(', num2str(single(v)), ')']; % 更新粒子速度文本
planet.String = ['t=', num2str(i * dt)]; % 更新时间文本
drawnow; % 刷新图像
v0 = v; % 更新速度
p0 = p; % 更新位置
pause(0.005);
end基于解析式的Boris算法迭代函数:
function [v,p] = a2(p, v, E, B, dt, qm)
A = [0, B(3), -B(2); -B(3), 0, B(1); B(2), -B(1), 0]; % 磁场矩阵
C = (qm * E * dt / 2)'; % 电场向量
P=(eye(3)+qm*dt*A/2)/(eye(3)-qm*dt*A/2);
v=(P*(v'+C)+C)';%速度迭代
p=p+v*dt;
end基于最终迭代解析式的Boris算法迭代函数:
function [v,p] = a3(p, v, E, B, dt, qm)
v=[(B(1)^2-B(2)^2-B(3)^2)*dt^2*qm^2+4 2*dt*qm*(2*B(3)-B(1)*B(2)*dt*qm) -2*dt*qm*(2*B(2)+B(1)*B(3)*dt*qm)
-2*dt*qm*(2*B(3)+B(1)*B(2)*dt*qm) (-B(1)^2+B(2)^2-B(3)^2)*dt^2*qm^2+4 2*dt*qm*(2*B(1)-B(3)*B(2)*dt*qm)
2*dt*qm*(2*B(2)-B(1)*B(3)*dt*qm) -2*dt*qm*(2*B(1)+B(2)*B(3)*dt*qm) (-B(1)^2-B(2)^2+B(3)^2)*dt^2*qm^2+4
]/((B(1)^2+B(2)^2+B(3)^2)*dt^2*qm^2+4)*(v'+qm/2*dt*[E(1);E(2);E(3)])+qm/2*dt*[E(1);E(2);E(3)];
v=v';
p=p+v*dt;
end用到的磁场:(此磁场是两个磁偶极子分别在(1,0,0)、(-1,0,0),处产生的磁场叠加,具备一定条件的带电粒子运动轨迹将约束在两磁偶极子之间一定空间中)
function B=b(p)
x=p(1);y=p(2);z=p(3);
B=[(2*(x-1)^2-y^2-z^2)/power((x-1)^2+y^2+z^2,2.5)+(2*(x+1)^2-y^2-z^2)/power((x+1)^2+y^2+z^2,2.5)
3*(x-1)*y/power((x-1)^2+y^2+z^2,2.5)+3*(x+1)*y/power((x+1)^2+y^2+z^2,2.5)
3*(x-1)*z/power((x-1)^2+y^2+z^2,2.5)+3*(x+1)*z/power((x+1)^2+y^2+z^2,2.5)];
end

为什么用Boris算法?
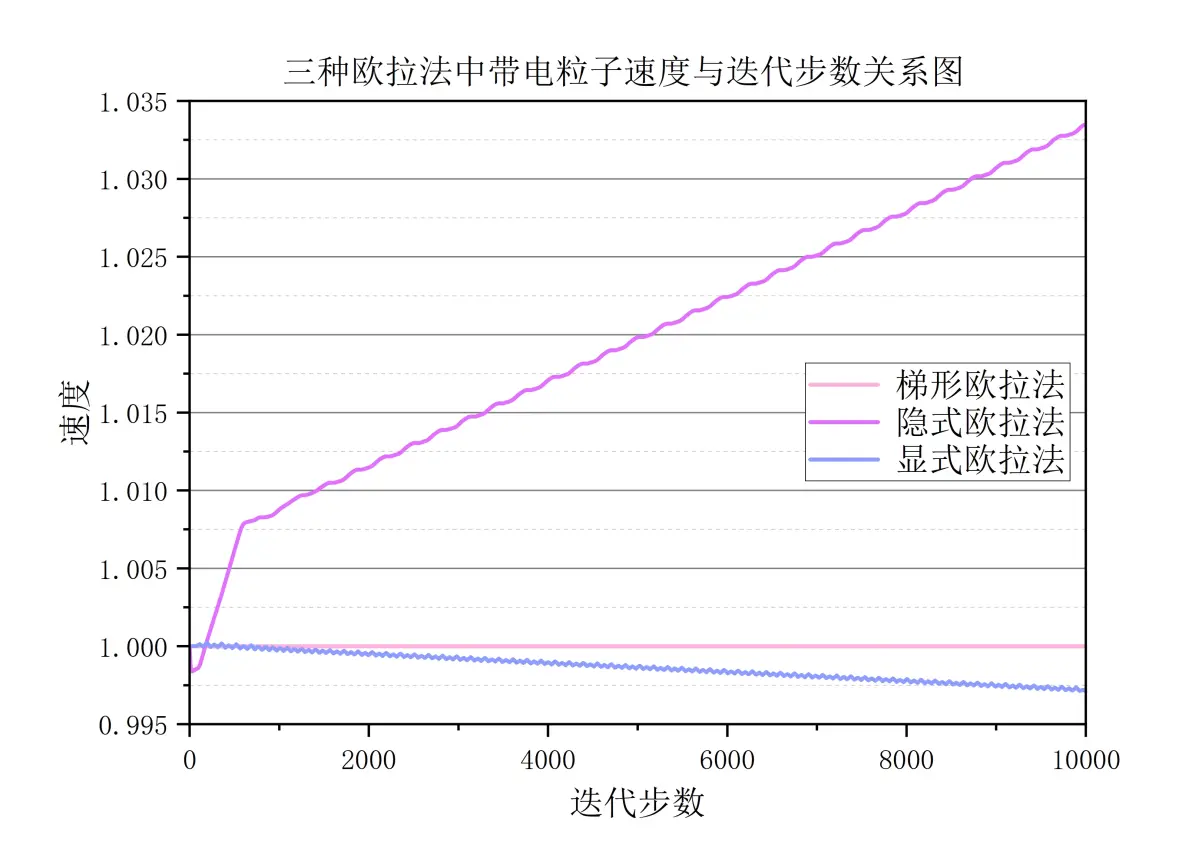
在磁场B=(0,0,1)和初始速度v=(1,0,1)、初始位置(-1,0,0)下,一个带电粒子(比荷q/m=+1)的圆周运动被用三种欧拉法模拟。速度随迭代步数的变化也被图示。结果显示,显式欧拉法(龙格库塔法)导致粒子能量逐渐耗散、轨迹半径缩小;而隐式欧拉法使粒子能量增加、半径扩大。Boris方法保持能量守恒和半径稳定,与解析解一致。 Boris方法具有保持相空间体积不变的特性,因此在长时间的模拟中比传统的龙格库塔法更稳定和准确。

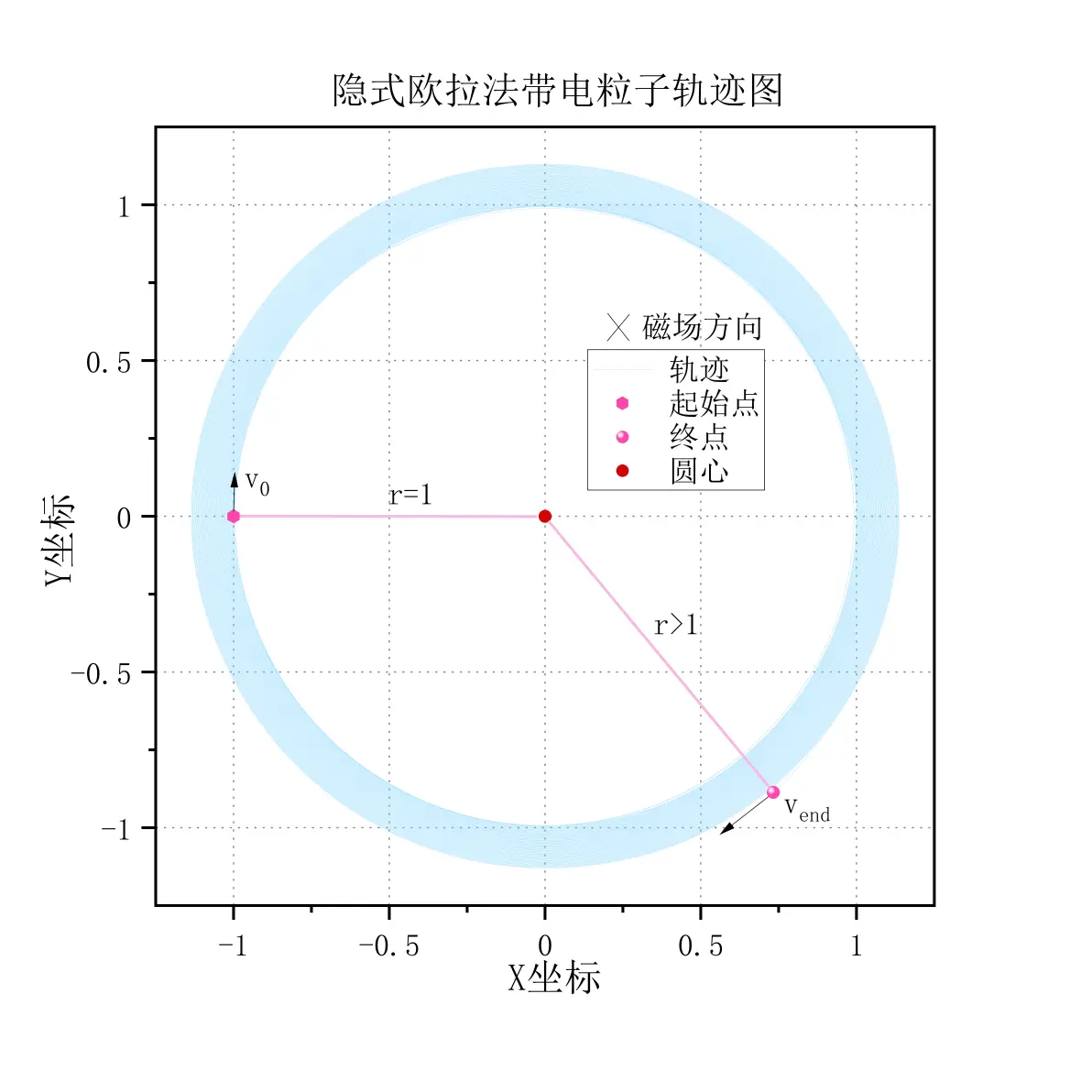
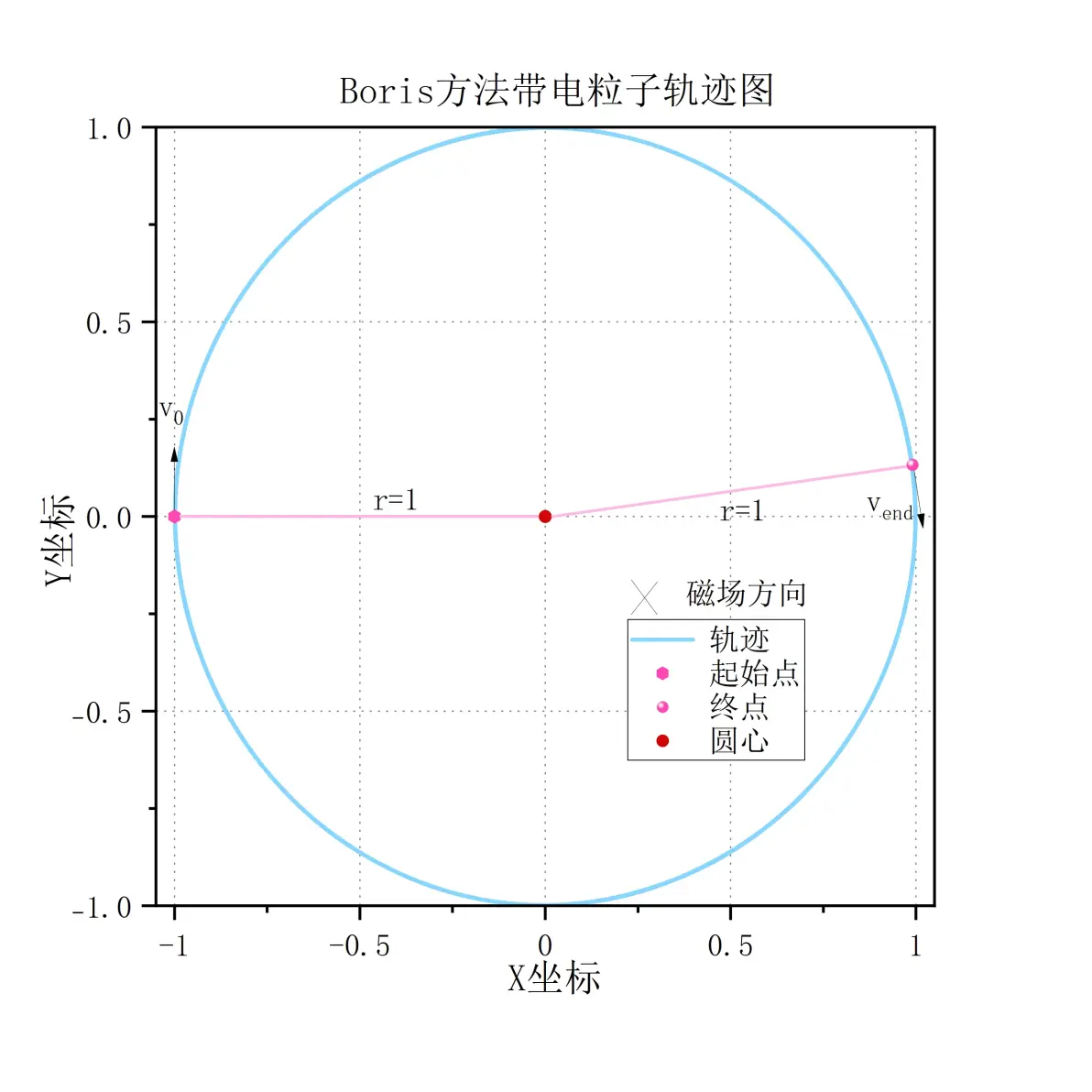
网页链接Reference
[1] Zhu L, Liu H , Wang X . Particle confinement property in the cusp-mirror field of a compact fusion reactor[J]. Physica Scripta, 2016, 91(9):095604.
[2] Winkel, Mathias, Speck, Robert, Ruprecht, Daniel. A high-order Boris integrator[J]. Journal of Computational Physics, 295:456-474.