云模型算法：MATLAB代码实现与解析

      云模型由中国工程院院士李德毅于1995年提出。云模型由若干云滴组成。其中每个云滴是确定的点，构成一个负责不确定的云。对于一个云的描述饱含三个元素，记作：（Ex，En，He）。

基本概念：Ex，云滴在论域空间的期望。

                 En，熵。用来表示云团的不确定性程度。

                 He，超熵。用来表示熵的不确定性程度。一个云模型记作。

                 正向云发生器：由（Ex，En，He）生成云团。

                 逆向云发生器：从复杂混乱云团中提取云的核心元素（Ex，En，He）。

主要目的：实现定性概念与定量描述直接的转换。

应用范围：自动驾驶、智能控制、复杂网络建模、语义控制、综合评价等

理论基础：概率论、模糊数学、混沌理论等

一、云模型定义

 在此参考

二、云发生器及Matlab代码：

2.1.正向云发生器

代码如下：

function [fval]=cloud_TO(Ex,En,He,N) %正向云发生器

% EX为生成云滴的均值

% En为生成云滴的熵

% He为生成云滴的超熵

% N为生成云滴数量

for i=1:N

    En_r(i)=randn(1)*He+En; %生成随机熵

    Ex_r(i)=randn(1)*En_r+Ex;

    fval(i)=exp(-(x(q)-Ex).^2./(2.*Enn.^2));

end

返回值是各云滴的隶属度。

2.2逆向云发生器

2.2.1  SBCT-1stM算法

SBCT-1stM是首个无确定度的逆向云算法，也是最初的算法，虽有有些过时，但对于云模型的理解很重要。

代码如下：

function [Ex,En,He]=cloud_SBCT_1thM(A)

Ex=mean(A);

En=mean(abs(A-Ex)).*sqrt(pi/2);

He=sqrt(var(A)-(En).^2);

end

2.2.2 SBCT-4stM算法

function [Ex,En,He]=cloud_SBCT_4stM(A)

Ex=mean(A);

S_2=var(A);

miu_4=(sum((Ex-A).^4))/(length(A)-1);

En=((9*S_2.^2-miu_4)/6).^(1/4);

He=sqrt(S_2-En);

end

2.2.3 MBCT-SR算法

       由于SBCT-1stM算法与SBCT-4stM算法都会出现超熵为虚数的情况，因此许昌林和王国胤提出了一种新算法MBCT-SR算法。

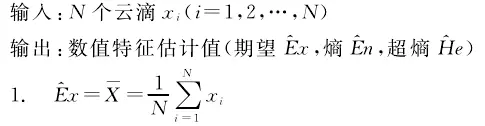
function [Ex,En,He]=cloud_MBCT_SR(A,n,m) %n为抽取样本个数，m为每个样本包含元素个数

Ex=mean(A);

for i=1:n

    X{i}=datasample(A,m);

    DY(i)=var(X{i});

end

En=sqrt(0.5*sqrt(4*mean(DY).^2-2*var(DY)));

He=sqrt(mean(DY)-En.^2);

2.3 关于三种逆向云发生器的双向认知研究成果

3. 其他

       关于云模型的相适应衡量方法、应用研究、瓶颈问题、外来展望等，感兴趣的小伙伴们可以看看杨洁等老师发表在计算机学报上的论文《正态云模型研究回顾与展望》

3.1 参考文献

[1] 杨洁,王国胤,刘群,郭毅可,刘悦,淦文燕,刘玉超.正态云模型研究回顾与展望[J].计算机学报,2018,41(03):724-744.

[2]卓金武等. Matlab在数学建模中的应用（第2版）[M].北京航空航天大学出版社:, 201409.324.

[3]刘常昱,冯芒,戴晓军,李德毅.基于云X信息的逆向云新算法[J].系统仿真学报,2004(11):2417-2420.

————————————————

版权声明：本文为CSDN博主「树梢上的少年」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。

原文链接：https://blog.csdn.net/weixin_43015468/article/details/118573781