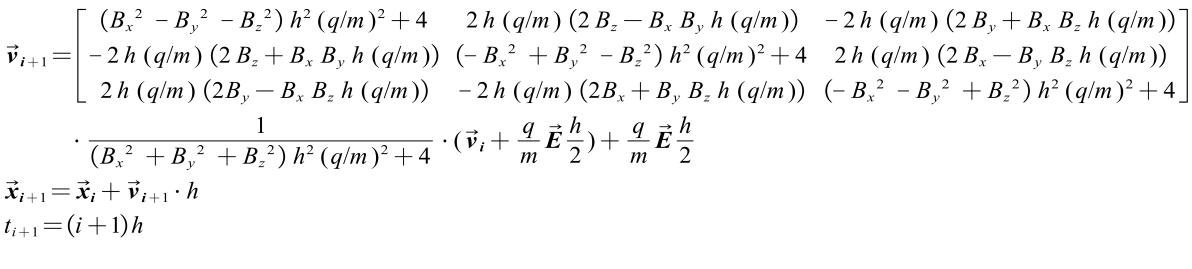matlab 代码:
%% parameters
q=1; m=1; g=0;%比荷 重力加速度
E=[ 1 1 0 ]; %Ex; Ey; Ez;
B=[2 0 0 ]; %Bx; By; Bz;
p0=[0 0 0 ] ; %x0=0; y0=0; z0=0; 粒子位置
v0=[0 1 0 ]; %vx0=0; vy0=1; vz0=0;
t=10*pi;dt=0.02;
colordef black;
figure('name','move');
colordef black;
grid on;
plane=scatter3(p0(1),p0(2),p0(3),'c','o');
planev=text(p0(1)+0.4,p0(2)+0.4,p0(3)+0.31,['v=','(',num2str(single(v0)),')']);
planep=text(p0(1)+0.4,p0(2)+0.4,p0(3)+0.205,['p=','(',num2str(single(p0)),')']);
planet=text(p0(1)+0.4,p0(2)+0.4,p0(3)+0.4,['t=','0']);
h=animatedline('color','b');
grid on
hold on
view(3)
xlabel('x')
ylabel('y')
zlabel('z')
hold on
tic
%% motion equation
for t=dt:t/dt+1
[v]=loca(p0,v0,E,B,g,dt,q/m);
p=p0+v*dt;
addpoints(h,p(1),p(2),p(3));
set(plane,'Xdata',p(1),'Ydata',p(2),'Zdata',p(3));
planep.String=['p=','(',num2str(single(p)),')'];
planev.String=['v=','(',num2str(single(v)),')'];
planet.String=['t=',num2str(t*dt)];
drawnow
%pause(0.005);
v0=v;
p0=p;
end
% drawnow
toc
%%%
function [v]=loca(p,v,E,B,g,dt,qm)
%此处加速度于位置p无关
A=[0,B(3),-B(2);-B(3),0,B(1);B(2),-B(1),0];
C=(qm*E*dt/2)'+[0,0,-g*dt/2]';
P=(eye(3)+qm*dt*A/2)/(eye(3)-qm*dt*A/2);
v=P*(v'+C)+C;%速度迭代
v=v';%转置
end

水字数!!!
速度迭代函数:
function [v]=loca(p,v,E,B,g,dt,qm)
%此处加速度于位置p无关
A=[0,B(3),-B(2);-B(3),0,B(1);B(2),-B(1),0];
C=(qm*E*dt/2)'+[0,0,-g*dt/2]';
P=(eye(3)+qm*dt*A/2)/(eye(3)-qm*dt*A/2);
v=P*(v'+C)+C;%速度迭代
v=v';%转置
end

迭代算法:
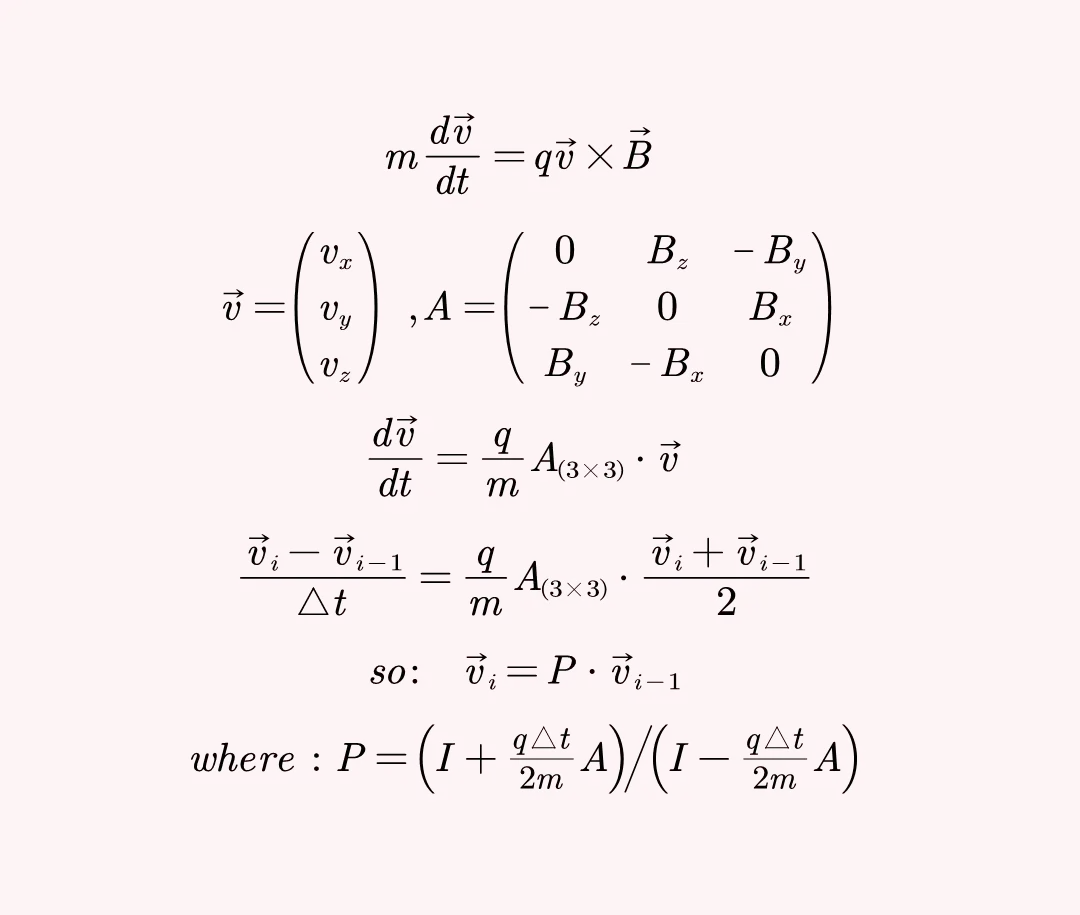
Boris 算法步骤
I是对角为1的单位矩阵,注意矩阵相除实际上是乘以分母矩阵的逆矩阵哦!
从第 i -1步递推到第 i 步, 电场力驱动的一 半首先作用在vi-1上获得 vi-1-, 再通过P矩阵计算得 到 vi-1+, 进一步将电场力驱动的一半加在vi-1+上,最终获得vi .
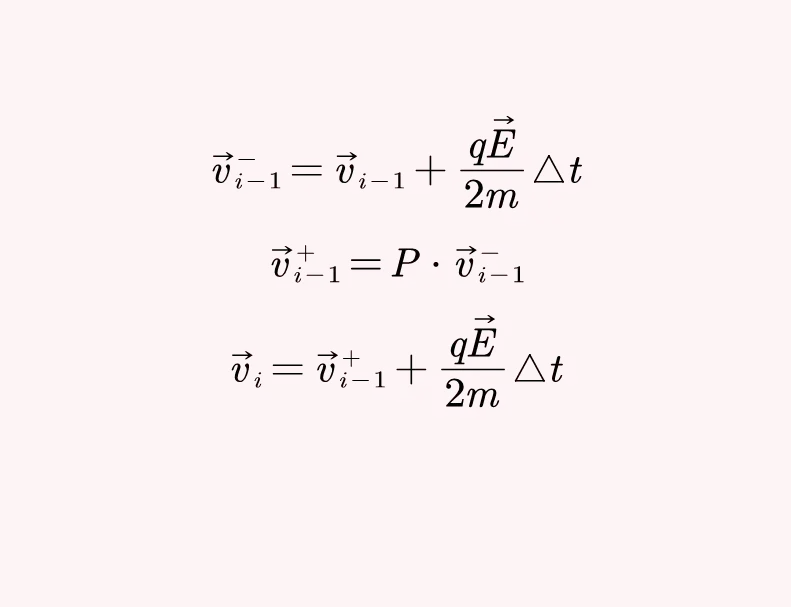
2023/12/1 更新
下面将以全新的角度介绍Boris算法:
可以通过以下运动方程来演化带电粒子的运动轨迹:
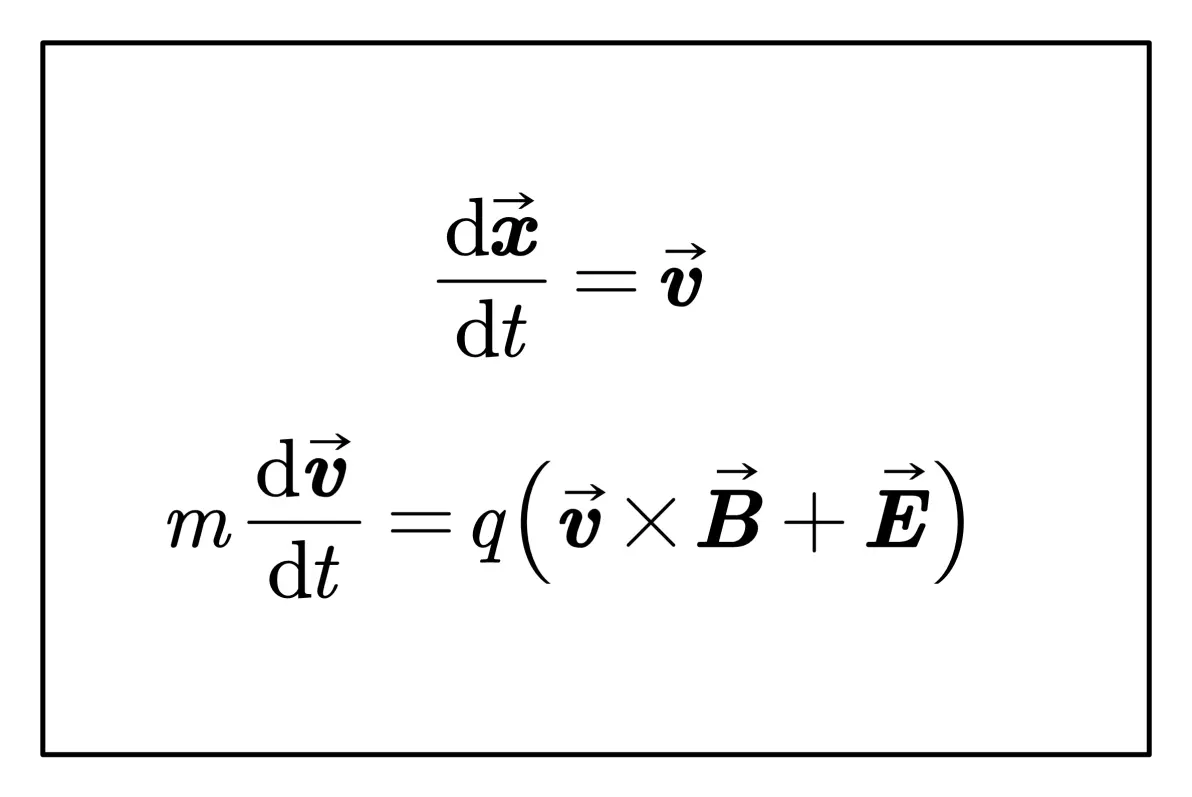
其中 B 为磁场强度, E 为电场强度. 以下是矩阵分量形式:

Boris 算法通过第 i 步相空间坐标求解第 i+1 步相空间坐标,上式可写为如下离散格式:
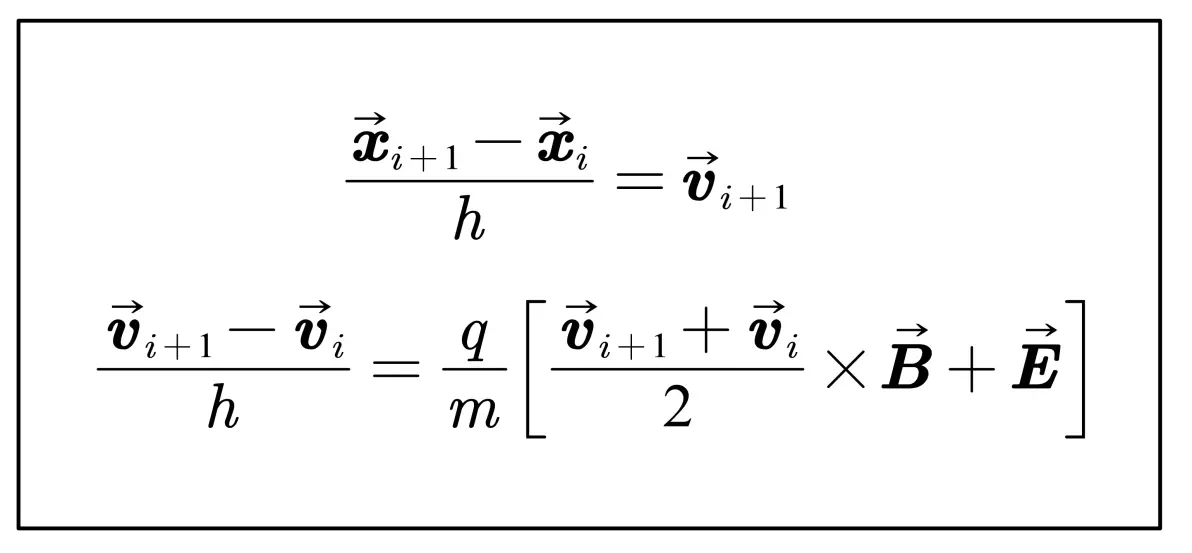
其中 h 为时间步长。在线性代数中,corss操作可以用矩阵相乘表示:
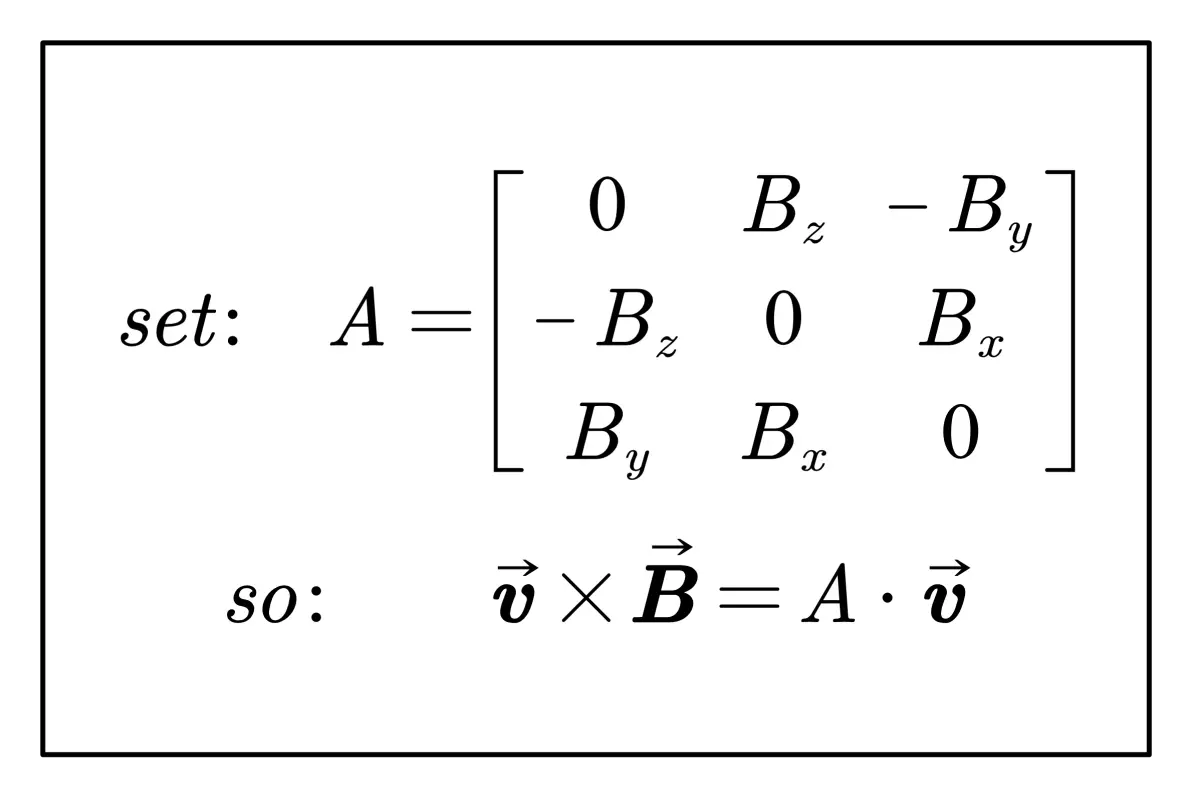
Boris 算法将电场力和磁场力分开计算,离散格式可以改写成如下格式:
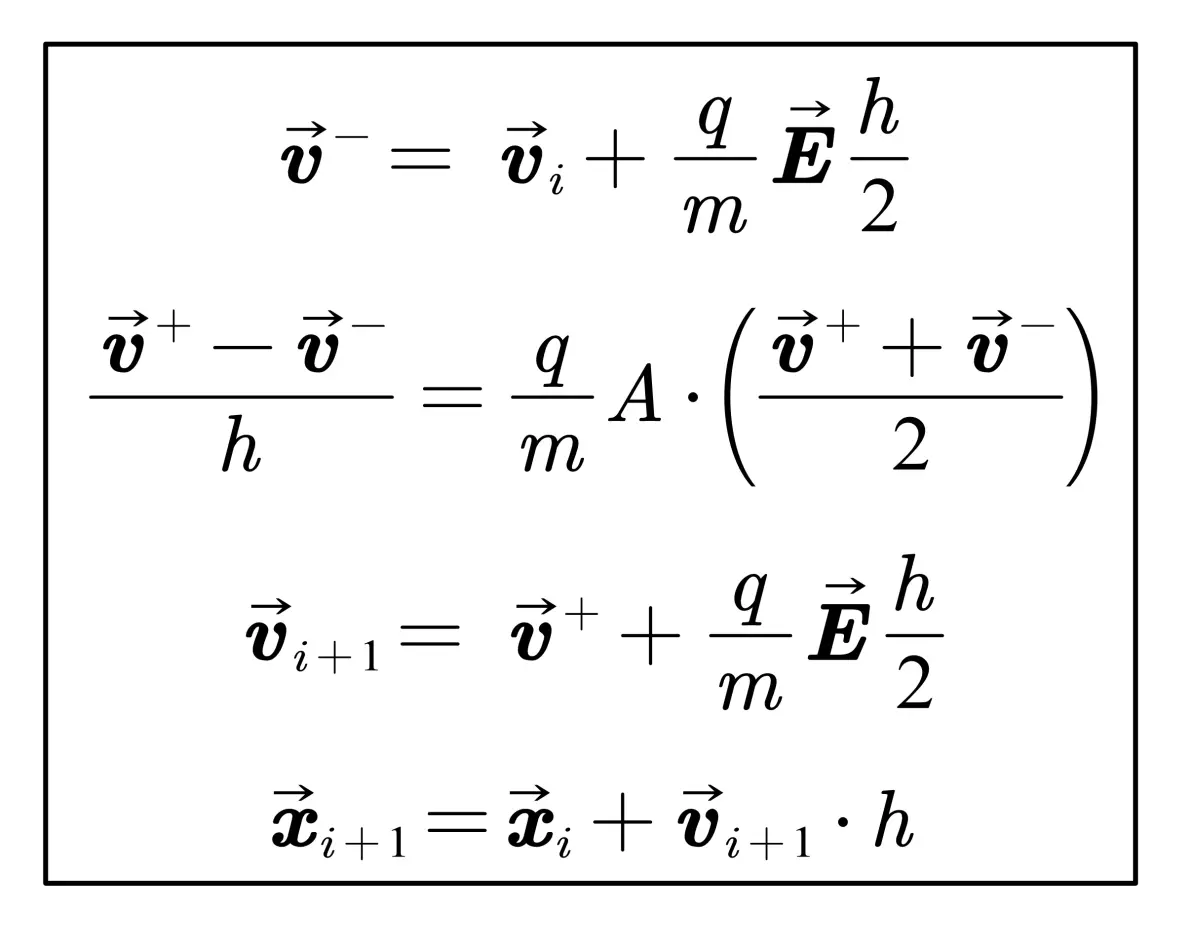
解析计算得到解析式:

I是对角为1的单位矩阵.第i 步递推到第 i+1步, 电场力驱动的一半首先作用在v_(i)上获得v-, 再通过P矩阵计算得到v+, 进一步将电场力驱动的一半加在上,最终获得v_(i+1).
另外,可以将P矩阵展开,将磁场代入,得到最终迭代解析式: