1. 面向对象程序设计简述
面向过程(Procedure Oriented,简称PO)思想即把求解的问题流程化,把一个复杂的大任务分解为小任务或子过程,子过程可继续划分,进而对子过程进行函数设计、编码实现;或者把一个算法分解为可解决的功能模块,或求解步骤流程化,按照功能模块或步骤进行程序设计。
面向对象(Object Oriented,简称OO)是一种程序设计思想。从20世纪60年代提出面向对象的概念到现在,它已经发展成为一种比较成熟的编程思想,并且逐步成为目前软件开发领域的主流技术。面向对象设计理念是一种从组织结构上模拟客观世界的方法。
面向对象程序设计是在面向过程程序设计的基础上发展而来的,它比面向过程编程具有更强的灵活性、扩展性。面向对象程序设计也是一个程序员发展的“分水岭”,读者应深刻理解面向对象设计的思想。
类(Class)和对象(Object)是面向对象编程(Object Oriented Programming,简称OOP)的核心概念:
类与对象的关系:类是一类事物的描述,是抽象的。对象是一类事物的实例,是具体的。类是对象的模板,对象是类的实体。类定义了一类对象有哪些属性和方法,但并没有实际的空间,实例化出的对象占有实际空间,用来存储成员变量。
注:算法从某种程度上来说,就是处理计算各种数据,算法可以说就是值的计算和处理。而变量作为数据的存储载体,在算法设计中无处不在,对象在实例化后,本质上就已经传递或存储了类属性数据。
总之,对于一个复杂的问题进行子问题的划分,面向过程把子问题设计为函数,数据在函数间通过参数交互,解决复杂问题;而面向对象,其对应的子问题可以设计为类并实例化为对象,对象拥有属性(数据)和方法(函数),对象之间通过组合和交互来解决问题。
本文基于数值分析与科学计算设计算法,相对于大型软件开发,其面向对象程序设计的思想并不复杂,主要涉及类的定义和设计,以及对象的实例化和调用。
2. MATLAB面向对象程序设计方法
以五种形式的牛顿迭代法求解非线性方程的近似解为例(参考 原理),说明MATLAB面向对象的设计流程、方法和思想。
(1)类的定义
关键字classdef 修饰,定义了牛顿迭代法类NewtonRoot(多个单词,每个单词首字母大写,“驼峰式”命名),同时继承handle类,使得能够在类内构造函数外修改属性并可不返回新变量。
classdef NewtonRoot < handle
%% 类的说明信息,可包括类的初始化信息,所具有的功能方法,使用方法等...(2)类的属性定义
关键字修饰properties,默认为公有属性,通过参数(Access=protected)设置访问权限。
%% 类的属性定义,皆设置为保护属性
properties(Access=protected)
% protected保护属性,不允许类外访问。而public为公有的属性,可以被访问。
equ_func % 表示待求(非)线性方程,要求是符号函数定义
x0 % 表示迭代求解的初值
eps =1e-10; % 近似解的精度要求
method = "newton" % 求解牛顿法的形式:simplify,newton, halley ,downhill 和multi_r
display = "final" % iter表示显示迭代过程的信息,final表示只显示最终迭代结果信息
max_iter = 200; % 最大迭代次数
fx % 方程的匿名函数形式
dfx % 方程的一阶导匿名函数形式
d2fx % 方程的二阶导匿名函数形式
end类的属性变量,用于存储数据,便于对象和方法之间数据的传递、共享和计算。对于牛顿迭代法求解非线性方程,其问题本身应该包括待求方程equ_func、初值x0等,除此之外,在各方法间涉及到方程一阶导数和二阶导数的计算。
对于属性定义,说明如下:
(3)类的方法定义
关键字methods修饰,默认公有属性,通过参数(Access=protected)设置访问权限。
%% methods关键字修饰,如下为类的行为方法,包括公有方法和保护方法
methods % 如下方法默认为公有属性,包含类的初始化和类属性的设置以及牛顿法核心函数1)类的构造方法
类的构造方法是对象实例化的第一步操作,负责创建类的对象,初始化对象的属性。构造函数与类名相同,一个类的定义中只能有一个构造函数。如下代码所示,主要包括类属性的初始化、类属性的健壮性检验、必要属性的初始化计算等。
此处类的构造函数的输出参数限制为self,即表示类对象本身。可以使用其他名称,如obj,但在类的整个定义中应统一,本文统一采用self。
%% 类的初始化以及参数的分析处理
function self = NewtonRoot(equ_func,x0, varargin)
% 必要参数:equ_func,x0。varargin为可变参数
if nargin < 2
error("输入参数不足,请输入完整参数equ_func和x0....")
end
if class(equ_func) ~= "sym"
error("缺失参数 equ_func 或参数 equ_func 类型定义错误...")
end
if class(x0) ~= "double"
error("缺失参数 x0 或参数 x0 定义错误...")
end
self.equ_func =equ_func;
self.x0 = x0;
args = inputParser; % 函数的输入解析器
addParameter(args, 'method', "newton"); % 设置牛顿法的求解形式,默认值普通newton法
addParameter(args, 'eps', 1e-10); % 设置求解精度参数eps,默认值1e-10
addParameter(args, 'display', 'final'); % 设置是否显示迭代过程参数display,默认值final,可为iter
addParameter(args, 'max_iter', 200); % 设置最大迭代次数参数max_iter,默认值200
parse(args,varargin{:}); % 对输入变量进行解析,如果检测到前面的变量被赋值,则更新变量取值
self.method = args.Results.method; % 求解方法
self.eps = args.Results.eps; % 若未传参,精度获取默认值
self.display = args.Results.display; % 是否显示迭代过程
self.max_iter = int16(args.Results.max_iter); % 若未传参,最大迭代次数获取默认值
[self.fx, self.dfx, self.d2fx] = self.solve_diff_fun(); % 类初始化时,即调用方法求解方程的一阶导二阶导
end2)setXXX和getXXX方法
由于类的属性访问权限的设置,对象不能直接访问类的属性,但可以通过setXXX和getXXX所提供的方法进行访问。主要指通过对象访问类属性(getXXX)和修改类属性值(setXXX),并在修改参数值时进行必要的参数检验和断言。
注意:每个方法的第一个参数限定为self。以供对象点调用。
%% 修改类的属性值,只有句柄类可以使用,定义类时使用 < handle
function setmethod(self, method)
self.method=method;
end
function seteps(self, eps)
% 参数的设置可进行健壮性的判断
if eps < 0
self.eps = 1e-10;
warning("近似根的精度要求不能为负数,此处设置默认为1e-10")
else
self.eps=eps;
end
end
function setdisplay(self, display)
self.display=display;
end
function setmax_iter(self, max_iter)
self.max_iter=max_iter;
end
function setx0(self, x0)
self.x0=x0;
end
function setequ_func(self, equ_func)
self.equ_func=equ_func;
[self.fx, self.dfx, self.d2fx] = self.solve_diff_fun(); % 重新调用
end
%% 此类不再提供其他类属性的get方法,可自行设计,以如下为例
function method = getmethod(self)
method = self.method;
end3)类方法
注意:该方法的输入参数限制为self,以供对象点调用。其他参数是设置可根据实际所解决的问题设置。可以在类定义中仅给出函数的声明,将函数的实现放到一个单独的文件中,但构造函数、析构函数、static(静态)函数除外。
%% 核心算法求解方程的近似根,包括方法的选择,显示信息与输出参数的构造
function varargout = solve_newton(self)
% 1. 根据所采用的求解方法method选择对应的牛顿法形式求解
% 2. 根据参数display,显示迭代过程或迭代结果信息
% 3. 输出参数结构体的构造和输出参数的判别
end % solve_newton4)类的其他方法
本例中,定了六个保护属性protected的方法,实例化的对象不能直接调用。
methods(Access=protected) % 如下求解方法为保护属性,不允许类外调用
%% 求符号方程的一阶导和二阶导,并转换为匿名函数,方便计算
function [equ_expr, diff_equ, diff2_equ] = solve_diff_fun(self)
end
%% 1 牛顿法求解
function iter_info = newton(self)
end % newton
%% 2 牛顿—哈利法法求解
function iter_info = newton_halley(self)
end % newton_halley
%% 3 简化牛顿法求解
function iter_info = simplify_newton(self)
end % simplify_newton
%% 4 牛顿下山法求解
function [iter_info, downhill_lambda] = newton_downhill(self)
end % newton_downhill
%% 5 牛顿法重根情形求解
function iter_info = newton_multi_root(self)
end % newton_multi_root
end % method3. MATLAB面向对象程序设计完整代码(牛顿迭代法)
classdef NewtonRoot < handle
%% 牛顿法求解方程的根:包含简化牛顿法 simplify ,牛顿法 newton ,牛顿加速哈利法 halley ,牛顿下山法 downhill 和重根情形 multi_r 。
% 更多使用方法:https://www.mathworks.com/help/releases/R2020b/matlab/matlab_oop/developing-classes-typical-workflow.html
% 类的初始化说明:
% 1. 必要参数:equ_func表示待求(非)线性方程,要求是符号函数定义;x0表示迭代求解的初值
% 2. varargin 表示可变参数,关键字形式传递,若未设置,则按照默认值。
% 可通过类中提供的set方法重设或修改类属性的值
% varargout = solve_newton()函数的输出参数varargout为可变参数:
% 1 如果输出参数为3个,则第1个参数为近似解,第2个参数为近似解的精度误差,第3个参数为退出条件
% 2 如果输出参数为2个,则第1个参数为近似解,第2个参数为近似解的精度误差
% 3 如果输出参数为1个,则表示牛顿法求解的结构体,包括各种迭代过程中的信息
%% 类的属性定义,皆设置为保护属性
properties(Access=protected)
% protected保护属性,不允许类外访问。而public为公有的属性,可以被访问。
equ_func % 表示待求(非)线性方程,要求是符号函数定义
x0 % 表示迭代求解的初值
eps =1e-10; % 近似解的精度要求
method = "newton" % 求解牛顿法的形式:simplify,newton, halley ,downhill 和multi_r
display = "final" % iter表示显示迭代过程的信息,final表示只显示最终迭代结果信息
max_iter = 200; % 最大迭代次数
fx % 方程的匿名函数形式
dfx % 方程的一阶导匿名函数形式
d2fx % 方程的二阶导匿名函数形式
end
%% methods关键字修饰,如下为类的行为方法,包括公有方法和保护方法
methods % 如下方法默认为公有属性,包含类的初始化和类属性的设置以及牛顿法核心函数
%% 类的初始化以及参数的分析处理
function self = NewtonRoot(equ_func,x0, varargin)
% 必要参数:equ_func,x0。varargin为可变参数
if nargin < 2
error("输入参数不足,请输入完整参数equ_func和x0....")
end
if class(equ_func) ~= "sym"
error("缺失参数 equ_func 或参数 equ_func 类型定义错误...")
end
if class(x0) ~= "double"
error("缺失参数 x0 或参数 x0 定义错误...")
end
self.equ_func =equ_func;
self.x0 = x0;
args = inputParser; % 函数的输入解析器
addParameter(args, 'method', "newton"); % 设置牛顿法的求解形式,默认值普通newton法
addParameter(args, 'eps', 1e-10); % 设置求解精度参数eps,默认值1e-10
addParameter(args, 'display', 'final'); % 设置是否显示迭代过程参数display,默认值final,可为iter
addParameter(args, 'max_iter', 200); % 设置最大迭代次数参数max_iter,默认值200
parse(args,varargin{:}); % 对输入变量进行解析,如果检测到前面的变量被赋值,则更新变量取值
self.method = args.Results.method; % 求解方法
self.eps = args.Results.eps; % 若未传参,精度获取默认值
self.display = args.Results.display; % 是否显示迭代过程
self.max_iter = int16(args.Results.max_iter); % 若未传参,最大迭代次数获取默认值
[self.fx, self.dfx, self.d2fx] = self.solve_diff_fun(); % 类初始化时,即调用方法求解方程的一阶导二阶导
end
%% 修改类的属性值,只有句柄类可以使用,定义类时使用 < handle
function setmethod(self, method)
self.method=method;
end
function seteps(self, eps)
% 参数的设置可进行健壮性的判断
if eps < 0
self.eps = 1e-10;
warning("近似根的精度要求不能为负数,此处设置默认为1e-10")
else
self.eps=eps;
end
end
function setdisplay(self, display)
self.display=display;
end
function setmax_iter(self, max_iter)
self.max_iter=max_iter;
end
function setx0(self, x0)
self.x0=x0;
end
function setequ_func(self, equ_func)
self.equ_func=equ_func;
[self.fx, self.dfx, self.d2fx] = self.solve_diff_fun(); % 重新调用
end
%% 此类不再提供其他类属性的get方法,可自行设计,以如下为例
function method = getmethod(self)
method = self.method;
end
%% 核心算法求解方程的近似根,包括方法的选择,显示信息与输出参数的构造
function varargout = solve_newton(self)
% 根据所采用的求解方法method选择对应的牛顿法形式求解
if lower(self.method) == "newton"
method_message = "普通牛顿迭代法";
iter_info = self.newton(); % 普通牛顿法
elseif lower(self.method) == "halley"
method_message = "牛顿—哈利迭代法";
iter_info = self.newton_halley(); % 牛顿—哈利法
elseif lower(self.method) == "simplify"
method_message = "简化的牛顿迭代法";
iter_info = self.simplify_newton(); % 简化牛顿法
elseif lower(self.method) == "downhill"
method_message = "牛顿下山迭代法";
[iter_info, downhill_lambda] = self.newton_downhill(); % 牛顿下山法
elseif lower(self.method) == "multi_r"
method_message = "牛顿重根情形迭代法";
iter_info = self.newton_multi_root(); % 牛顿重根情形
else
warning("牛顿法仅限于【newton、halley、simple、downhill和multi_r】之一,此处采用牛顿法求解!")
method_message = "普通牛顿迭代法";
iter_info = self.newton(); % 普通牛顿法
end
% 根据参数display,显示迭代过程或迭代结果信息
if lower(self.display) == "iter"
disp(method_message)
disp(array2table(iter_info, 'VariableNames', ["IterNums", "ApproximateSol", "ErrorPrecision"]))
elseif lower(self.display) == "final"
fprintf(method_message + ":IterNum = %d, ApproximateSolution = %.15f, ErrorPrecision = %.15e\n", ...
iter_info(end, 1), iter_info(end, 2), iter_info(end, 3));
else
warning("参数display仅限于【iter、final】之一!")
end
% 输出参数结构体的构造
sol.ApproximateSolution = iter_info(end, 2); % 数值近似解
sol.ErrorPrecision =iter_info(end, 3); % 数值近似解误差
sol.NumerOfIterations = length(iter_info); % 迭代次数
sol.NewtonMethod = self.method; % 所采用的方法
sol.IntrationProcessInfomation = iter_info; % 迭代过程信息
if length(iter_info) == self.max_iter
sol.info = "已达最大迭代次数";
end
if length(iter_info) < self.max_iter
sol.convergence = "收敛到满足精度的近似解";
else
sol.convergence = "精度过高,或未收敛到满足精度的解,增大迭代次数或修改初值或降低精度要求";
end
if lower(self.method) == "downhill"
sol.DownhillLambda = downhill_lambda;
end
% 输出参数的判别
if nargout == 3
varargout{1} = iter_info(end, 2);
varargout{2} = iter_info(end, 3);
if length(iter_info) == self.max_iter
varargout{3} = 0; % 退出标记
else
varargout{3} = 1; % 退出标记
end
elseif nargout == 2
varargout{1} = iter_info(end, 2);
varargout{2} = iter_info(end, 3);
elseif nargout == 1
varargout{1} = sol;
elseif nargout == 0
varargout{1} = iter_info(end, 2);
else
error("输出参数最多为3个....")
end
end % solve_newton
end % method
methods(Access=protected) % 如下求解方法为保护属性,不允许类外调用
%% 求符号方程的一阶导和二阶导,并转换为匿名函数,方便计算
function [equ_expr, diff_equ, diff2_equ] = solve_diff_fun(self)
x = symvar(self.equ_func); % 获取符号函数的变量
equ_expr = matlabFunction(self.equ_func); % 原符号方程转换为匿名函数
diff_equ = matlabFunction(diff(self.equ_func, x, 1)); % 一阶导数方程,并转换为匿名函数
diff2_equ = matlabFunction(diff(self.equ_func, x, 2)); % 二阶导数方程,并转换为匿名函数
end
%% 1 牛顿法求解
function iter_info = newton(self)
var_iter = 0; % 迭代次数变量
sol_tol = self.fx(self.x0); % 方程在当前迭代值的精度,初始为初值时的精度
if abs(sol_tol) < self.eps
iter_info = [1, self.x0, sol_tol];
return
end
x_cur = self.x0; % 迭代过程中的对应于x_(k)
iter_info =zeros(self.max_iter, 3); % 存储迭代过程信息,思考如何预分配内存?
% 算法具体迭代多少次,不清楚,故用while。可用for循环,在循环体内,满足精度要求退出循环
while abs(sol_tol) > self.eps && var_iter < self.max_iter
var_iter = var_iter + 1; % 迭代次数增一
x_next = x_cur - self.fx(x_cur) / self.dfx(x_cur); % 牛顿迭代公式
sol_tol = self.fx(x_next); % 新值的精度
x_cur = x_next; % 近似根的迭代更替
iter_info(var_iter, :) = [var_iter, x_next, sol_tol];
end
if var_iter < self.max_iter
iter_info(var_iter + 1:end, :) = []; % 删除未赋值的区域
end
end % newton
%% 2 牛顿—哈利法法求解
function iter_info = newton_halley(self)
var_iter = 0; % 迭代次数变量
sol_tol = self.fx(self.x0); % 方程在当前迭代值的精度,初始为初值时的精度
if abs(sol_tol) < self.eps
iter_info = [1, self.x0, sol_tol];
return
end
x_cur =self. x0; % 迭代过程中的对应于x_(k)
iter_info =zeros(self.max_iter, 3); % 存储迭代过程信息
while abs(sol_tol) > self.eps && var_iter < self.max_iter
var_iter = var_iter + 1; % 迭代次数增一
fval = self.fx(x_cur); % 当前近似解的方程精度
df_val = self.dfx(x_cur); % 当前近似解的方程一阶导数精度
d2f_val = self.d2fx(x_cur); % 当前近似解的方程二阶导数精度
x_next = x_cur - fval / df_val / (1 - fval * d2f_val / (2* df_val^2)); % 牛顿哈利迭代公式
sol_tol = self.fx(x_next); % 新值的精度
x_cur = x_next; % 近似根的迭代更替
iter_info(var_iter, :) = [var_iter, x_next, sol_tol];
end
if var_iter < self.max_iter
iter_info(var_iter + 1:end, :) = []; % 删除未赋值的区域
end
end % newton_halley
%% 3 简化牛顿法求解
function iter_info = simplify_newton(self)
var_iter = 0; % 迭代次数变量
lambda = 1 / self.dfx(self.x0); % 简化牛顿法的常数
sol_tol = self.fx(self.x0); % 方程在当前迭代值的精度,初始为初值时的精度
if abs(sol_tol) < self.eps
iter_info = [1, self.x0, sol_tol];
return
end
x_cur = self.x0; % 迭代过程中的对应于x_(k)
iter_info =zeros(self.max_iter, 3); % 存储迭代过程信息,思考如何预分配内存?
while abs(sol_tol) > self.eps && var_iter < self.max_iter
var_iter = var_iter + 1; % 迭代次数增一
x_next = x_cur - lambda * self.fx(x_cur); % 简化牛顿迭代公式
sol_tol = self.fx(x_next); % 新值的精度
x_cur = x_next; % 近似根的迭代更替
iter_info(var_iter, :) = [var_iter, x_next, sol_tol];
end
if var_iter < self.max_iter
iter_info(var_iter + 1:end, :) = []; % 删除未赋值的区域
end
end % simplify_newton
%% 4 牛顿下山法求解
function [iter_info, downhill_lambda] = newton_downhill(self)
var_iter = 0; % 迭代次数变量
sol_tol = self.fx(self.x0); % 方程在当前迭代值的精度,初始为初值时的精度
if abs(sol_tol) < self.eps
iter_info = [1, self.x0, sol_tol];
return
end
x_cur = self.x0; % 迭代过程中的对应于x_(k)
iter_info =zeros(self.max_iter, 3); % 存储迭代过程信息,思考如何预分配内存?
downhill_lambda = ones(self.max_iter); % 存储下山因子
while abs(sol_tol) > self.eps && var_iter < self.max_iter
var_iter = var_iter + 1; % 迭代次数增一
f_val = self.fx(x_cur); % 当前近似解的方程精度
df_val = self.dfx(x_cur); % 当前近似解的方程一阶导数精度
x_next = x_cur - f_val / df_val; % 牛顿迭代公式
sol_tol = self.fx(x_next); % 新值的精度
% 判别是否满足下降条件
while abs(sol_tol) > abs(f_val)
downhill_lambda(var_iter) = downhill_lambda(var_iter) / 2; % 下山因子减半
x_next = x_cur - downhill_lambda(var_iter) * f_val / df_val; % 牛顿下山迭代公式
sol_tol = self.fx(x_next); % 新值的精度
end
x_cur = x_next; % 近似根的迭代更替
iter_info(var_iter, :) = [var_iter, x_next, sol_tol];
end
if var_iter < self.max_iter
iter_info(var_iter + 1:end, :) = []; % 删除未赋值的区域
downhill_lambda(var_iter + 1:end) = []; % 删除未赋值的区域
end
end % newton_downhill
%% 5 牛顿法重根情形求解
function iter_info = newton_multi_root(self)
var_iter = 0; % 迭代次数变量
sol_tol = self.fx(self.x0); % 方程在当前迭代值的精度,初始为初值时的精度
if abs(sol_tol) < self.eps
iter_info = [1, self.x0, sol_tol];
return
end
x_cur = self.x0; % 迭代过程中的对应于x_(k)
iter_info =zeros(self.max_iter, 3); % 存储迭代过程信息,思考如何预分配内存?
while abs(sol_tol) > self.eps && var_iter < self.max_iter
var_iter = var_iter + 1; % 迭代次数增一
fval = self.fx(x_cur); % 当前近似解的方程精度
df_val = self.dfx(x_cur); % 当前近似解的方程一阶导数精度
d2f_val = self.d2fx(x_cur); % 当前近似解的方程二阶导数精度
x_next = x_cur -fval * df_val / (df_val^2 - fval * d2f_val); % 牛顿重根情形迭代公式
sol_tol = self.fx(x_next); % 新值的精度
x_cur = x_next; % 近似根的迭代更替
iter_info(var_iter, :) = [var_iter, x_next, sol_tol];
end
if var_iter < self.max_iter
iter_info(var_iter + 1:end, :) = []; % 删除未赋值的区域
end
end % newton_multi_root
end % method
end % NewtonRoot4. MATLAB面向对象程序设计——测试调用
具体实例参考 牛顿迭代法的面向过程设计
(1)对象的实例化
对象的实例化为OOP的第一步,然后才能通过对象调用其他方法。如下代码所示,实例化后,对象拥有类定义的所有属性变量和方法。必要参数必须传递,可变参数通过关键字参数Name-Value的形式传递(如"display", "iter")。
syms x
% equ_func = 2 * exp(-x) * sin(x) + 2 * cos(x) - 0.25; % 非线性方程1
equ_func = (x - 1) * (sin(x - 1) + 3 * x) - x^3 + 1; % 非线性方程2
% equ_func = 2 * exp(-x) * sin(x); % 非线性方程3
x0 = 1.5; % 初值设置
nt_obj = NewtonRoot(equ_func, x0, "display", "iter", "eps", 1e-16, "method", "newton"); % 对象实例化(2)对象访问类属性
由于类类型定义时,其访问权限为保护属性protected,不允许类外调用,即使是实例化的对象。如显示对象nt_obj,命令行窗口显示如下:
>> nt_obj
nt_obj =
NewtonRoot (不具有属性)。如图1所示,当前实例化的对象尽可访问的属性或方法仅仅是定义为公有属性的方法。

图1 当前实例化对象可访问的方法
但可以通过类方法所提供的getXXX和setXXX方法访问和修改类属性变量的值。对象访问类方法的方法为“对象名.方法名()”
>> nt_obj.getmethod()
ans =
"newton"
>> nt_obj.setmax_iter(300)现修改类属性的访问权限为public,则实例化后,对象可以显示所有属性信息,且对象可以直接访问类的所有属性。通常情况下,类属性定义为私有属性或保护属性。
>> nt_obj = NewtonRoot(equ_func, x0, "display", "iter", "eps", 1e-16, "method", "newton"); % 对象实例化
>> nt_obj
nt_obj =
NewtonRoot - 属性:
equ_func: [1×1 sym]
x0: 1.5000
eps: 1.0000e-16
method: "newton"
display: "iter"
max_iter: 200
fx: @(x)(x.*3.0+sin(x-1.0)).*(x-1.0)-x.^3+1.0
dfx: @(x)x.*3.0+sin(x-1.0)+(cos(x-1.0)+3.0).*(x-1.0)-x.^2.*3.0
d2fx: @(x)x.*-6.0+cos(x-1.0).*2.0-sin(x-1.0).*(x-1.0)+6.0(3)对象调用方法
由于类方法solve_newton除self外无其他参数,可不传参,此处省略(),若有除self外的参数,则必须传参(args)。
sol_newton = nt_obj.solve_newton; % 通过实例化的对象调用类公有方法
% sol_newton = nt_obj.solve_newton(); % 也可以采用添加()形式调用通过调用setmethod(method)修改牛顿法的迭代形式,求解不同情形下的非线性方程的近似解。
nt_obj.setmethod("halley") % 修改牛顿法为哈利法
sol_halley = nt_obj.solve_newton; % 此时调用,则采用牛顿—哈利法求解近似解(4)完整测试代码,命名文件名为“test_newton_root_object”
% clc, clear
syms x
% equ_func = 2 * exp(-x) * sin(x) + 2 * cos(x) - 0.25; % 非线性方程1
equ_func = (x - 1) * (sin(x - 1) + 3 * x) - x^3 + 1; % 非线性方程2
% equ_func = 2 * exp(-x) * sin(x); % 非线性方程3
x0 = 1.5; % 初值设置
nt_obj = NewtonRoot(equ_func, x0, "display", "iter", "eps", 1e-16, "method", "newton"); % 对象实例化
sol_newton = nt_obj.solve_newton; % 通过实例化的对象调用类公有方法
nt_obj.setmethod("halley") % 修改牛顿法为哈利法
sol_halley = nt_obj.solve_newton; % 此时调用,则采用牛顿—哈利法求解近似解
nt_obj.setmethod("simplify") % 修改牛顿法为简化牛顿法
sol_simplify = nt_obj.solve_newton;
nt_obj.setmethod("downhill") % 修改牛顿法为牛顿下山法
sol_downhill = nt_obj.solve_newton;
nt_obj.setmethod("multi_r") % 修改牛顿法为重根情形下的迭代法
sol_multi_r = nt_obj.solve_newton;
% 如下为可视化近似解的收敛曲线
figure
plot(sol_newton.IntrationProcessInfomation(:, 1), sol_newton.IntrationProcessInfomation(:, 3), "o-", "LineWidth", 1)
hold on
plot(sol_halley.IntrationProcessInfomation(:, 1), sol_halley.IntrationProcessInfomation(:, 3), "s-", "LineWidth", 1)
% plot(sol_simplify.IntrationProcessInfomation(:, 1), sol_simplify.IntrationProcessInfomation(:, 3), "p-", "LineWidth", 1)
plot(sol_downhill.IntrationProcessInfomation(:, 1), sol_downhill.IntrationProcessInfomation(:, 3), "p-", "LineWidth", 1)
plot(sol_multi_r.IntrationProcessInfomation(:, 1), sol_multi_r.IntrationProcessInfomation(:, 3), "*-", "LineWidth", 1)
legend("newton:" + string(sol_newton.NumerOfIterations), "halley:" + string(sol_halley.NumerOfIterations), ...
"downhill:" + string(sol_downhill.NumerOfIterations), "multiroot:" + string(sol_multi_r.NumerOfIterations))
legend("boxoff")
grid on; grid minor
box off; hold off
axis([0, 30, -0.01, 0.1])
xlabel("Numer Of Iterations")
ylabel("Error Precision")
title("The Different Newton Method of Error Precision Curve")输出过程(简化的牛顿法不收敛):
>> test_newton_root_object
普通牛顿迭代法
IterNums ApproximateSol ErrorPrecision
________ ______________ ______________
1 0.81807 0.03894
2 0.90287 0.010335
3 0.94944 0.0026846
4 0.97413 0.00068624
......
22 1 1.0214e-14
23 1 2.5535e-15
24 1 6.6613e-16
25 1 1.1102e-16
26 1 0
牛顿—哈利迭代法
IterNums ApproximateSol ErrorPrecision
________ ______________ ______________
1 1.3299 0.070967
2 1.116 0.01187
3 1.0373 0.0013425
4 1.0123 0.00014936
5 1.0041 1.6598e-05
6 1.0014 1.8442e-06
7 1.0005 2.0491e-07
8 1.0002 2.2768e-08
9 1.0001 2.5298e-09
10 1 2.8109e-10
11 1 3.1232e-11
12 1 3.4702e-12
13 1 3.8558e-13
14 1 4.2744e-14
15 1 4.774e-15
16 1 6.6613e-16
17 1 0
简化的牛顿迭代法
IterNums ApproximateSol ErrorPrecision
________ ______________ ______________
1 0.81807 0.03894
2 0.58658 0.23675
3 -0.82082 7.8009
4 -47.195 1.119e+05
5 -6.6527e+05 2.9444e+17
6 -1.7504e+18 5.3626e+54
7 -3.1879e+55 3.2399e+166
8 -1.926e+167 Inf
9 -Inf NaN
牛顿下山迭代法
IterNums ApproximateSol ErrorPrecision
________ ______________ ______________
1 0.81807 0.03894
2 0.90287 0.010335
3 0.94944 0.0026846
4 0.97413 0.00068624
5 0.98691 0.00017365
......
22 1 1.0214e-14
23 1 2.5535e-15
24 1 6.6613e-16
25 1 1.1102e-16
26 1 0
牛顿重根情形迭代法
IterNums ApproximateSol ErrorPrecision
________ ______________ ______________
1 1.4028 0.092552
2 1.2257 0.039007
3 1.0467 0.0020761
4 1.0012 1.5218e-06
5 1 5.8431e-13
6 1 0各牛顿法的误差收敛曲线如图2所示,由于简化牛顿法不收敛或收敛较慢,故不再可视化。
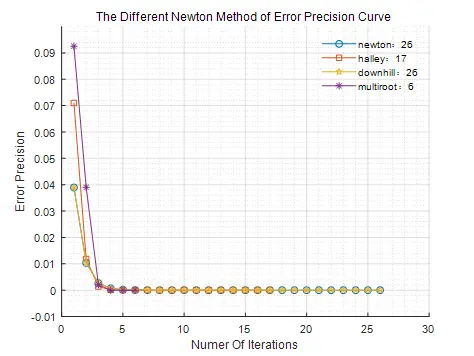
图2 各牛顿法的误差收敛曲线