基于MATLAB的牛顿-拉夫逊算法：电力系统潮流计算案例

一、实验学时：

6学时。

二、实验目的：

通过采用牛顿-拉夫逊法实现电力系统潮流计算的编程和仿真实验，强化学生对复杂电力系统潮流计算相关知识的理解，使学生具备通过MATLAB编程实现数值计算的能力，培养学生解决电力系统中复杂工程问题的能力。

三、实验原理：

电力系统分析的潮流计算是电力系统分析的一个重要的部分。通过对电力系统潮流分布的分析和计算，可进一步对系统运行的安全性，经济性进行分析、评估，提出改进措施。电力系统潮流的计算和分析是电力系统运行和规划工作的基础。潮流计算是指对电力系统正常运行状况的分析和计算。通常需要已知系统参数和条件，给定一些初始条件，从而计算出系统运行的电压和功率等；潮流计算方法很多：高斯-塞德尔法、牛顿-拉夫逊法、P-Q分解法、直流潮流法，以及由高斯-塞德尔法、牛顿-拉夫逊法演变的各种潮流计算方法。 采用牛顿-拉夫逊迭代法实现潮流计算的一般步骤： (1) 输入原始数据和信息：y、Pis、Qis、Uis、约束条件； (2) 形成节点导纳矩阵YB； (3) 设置各节点电压初值ei(0)、fi(0)或Ui(0)、δi(0)； (4) 将初始值代入直角坐标或极坐标形式的功率方程，求不平衡量ΔPi(0)、ΔQi(0)、ΔUi2(0)； (5) 计算雅可比矩阵各元素（Hij、Lij、Nij、Jij、Rij、Sij）； (6) 求解修正方程，解得Δei(k)、Δfi(k)或ΔUi(k)、Δδi(k)； (7) 求节点电压新值ei(k+1) = ei(k) + Δei(k)、fi(k+1) = fi(k) + Δfi(k)，或Ui(k+1) = Ui(k) + ΔUi(k)、δi(k+1) = δi(k) + Δδi(k)； (8) 判断是否收敛：Max|Δei(k)| ≤ ε，Max|Δfi(k)| ≤ ε或Max|ΔUi(k)| ≤ ε，Max|Δδi(k)| ≤ ε； (9) 重复迭代步骤(4)、(5)、(6)、(7)，直到满足步骤(8)的收敛条件； (10) 求平衡节点的功率和PV节点的Qi及各支路的功率。

四、实验要求：

1. 通过牛顿-拉夫逊法求非线性方程组近似解的MATLAB编程范例，理解实现牛顿-拉夫逊法的基本代码编写方法； 2. 根据给定的电力系统网络接线图、节点类型和具体参数，运用以极坐标形式的牛顿-拉夫逊法计算系统的潮流分布。

五、实验内容：

1. 牛顿-拉夫逊法求非线性方程组近似解范例

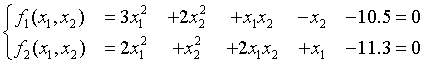
求解过程： 令

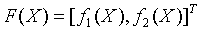
迭代次数为k。

F(X)的雅克比矩阵为

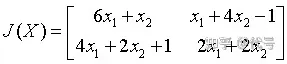
设初始近似解为

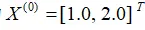
迭代精度取0.0001。 求解代码示例：

代码乱了，可看文档或知乎，见文末。

2. 采用牛顿-拉夫逊法实现电力系统潮流计算编程

网络接线如图1.1所示，各支路导纳均以标幺值标于图1.1中。其中： (1) 节点1、2、3、4为PQ节点，注入功率分别为：

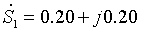
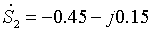
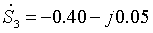
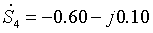
，节点1连接给定功率的发电厂；

(2) 节点5为平衡节点，电压保持为定值，V5 = 1.05； 试运用极坐标形式的牛顿-拉夫逊法计算该系统各节点的电压和各线路的功率。计算精度要求个节点电压修正量不大于10−5。

图1.1 电力系统接线图 程序编写提示： (1) 注意编写程序时节点编号应与图中对应，特别是平衡节点必须编为5号； (2) 在MATLAB中i和j是作为虚数单位，所以在编写代码时表示节点导纳矩阵的行号和列号的变量用m和n； (3) 极坐标形式的牛顿-拉夫逊法潮流计算相关公式：

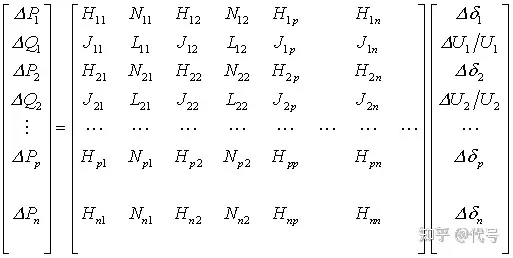
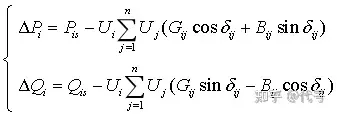
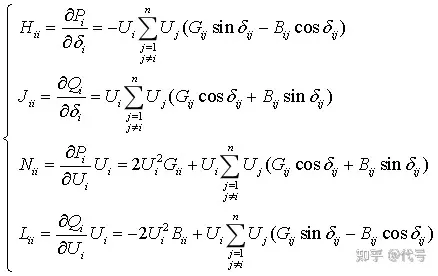
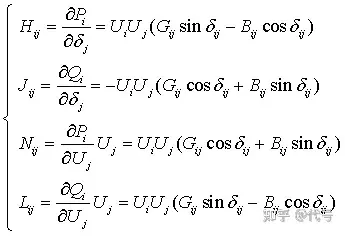
(4) 节点参数和导纳矩阵相关代码：

运行结果：

六、报告要求

(1) 画出程序流程图； (2) 给出雅克比矩阵参数求解、不平衡量求解、各条线路功率求解的关键代码； (3) 给出迭代过程中各节点电压的计算值； (4) 给出各条线路功率的计算结果。

七、报告

《电力系统基础》实验报告 姓名： 学号： 日期： 成绩： 实验名称：复杂电力系统的潮流计算编程 实验学时：6学时 实验内容： 1. 牛顿-拉夫逊法求非线性方程组近似解范例； 2. 采用牛顿-拉夫逊法实现电力系统潮流计算编程。 实验要求： 1. 通过MATLAB编程范例，理解实现牛顿-拉夫逊法的基本代码编写方法； 2. 根据给定的电力系统网络接线图、节点类型和具体参数，运用以极坐标形式的牛顿-拉夫逊法计算系统的潮流分布。 范例程序求解结果：迭代次数k = 6 ，结果x1 = 1.3478 ，x2 = 1.5045 。 潮流计算程序流程图：

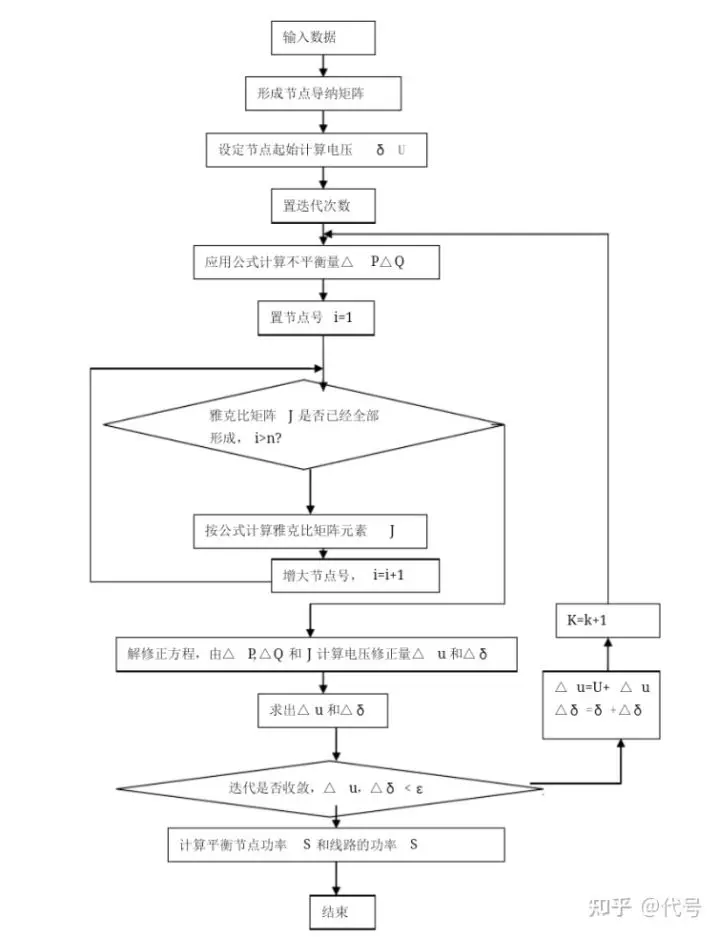
部分关键代码：

见上

潮流计算结果：

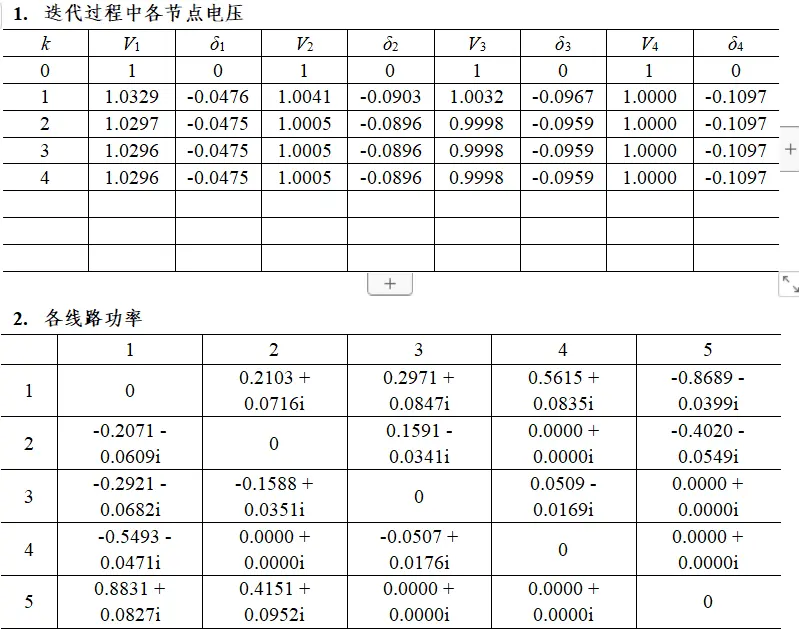
实验结果分析：

(1)本次课程设计让我从真正认识了牛顿拉夫逊计算潮流的方法,通过自己编程和同学一起讨论我会使用牛拉法求潮流了。首先最重要的就是建立节点导纳短阵,对于变压器和线路导纳的处理。会用编程语言实现。

(2)在编程以前要做好前提工作,分析题目,画好等值电路,求出各节点的导纳阻抗,还要分析好 PQ , PV 节点,没立平衡节点。身将平衡节点编号放到最大。

(3)从本次实例可以看出,牛拉法收敛速度快。结果精确(误差< 0.00001)。经过六次迭代就已经收敛。

代码请看：

基于MATLAB的牛顿-拉夫逊算法(极坐标)潮流计算算例（电力系统分析基础实验-附代码结果） - 知乎 (zhihu.com)