Matlab实现相移干涉三步算法与相位展开的个人经验分享‌

如下图所示，有三幅在时间序列上采集的干涉条纹图，三次相移量依次为0、2π/3和4π/3，根据三步算法公式，干涉条纹图的相位分布为：

三步算法计算公式（本题适用）

给定的三幅干涉条纹图

式（5.8）表示的相位分布处在-π/2~π/2的范围，这部分代码已在之前的视频中给出，如下所示：

clear all; close all; clc;

A1=im2double(imread('FringePattern1.tif'));%读取三幅干涉条纹图

A2=im2double(imread('FringePattern2.tif'));

A3=im2double(imread('FringePattern3.tif'));

S=sqrt(3)*(A3-A2);%公式（5.8）等号右侧分子

C=2*A1-A2-A3;%公式（5.8）等号右侧分母

delta=atan(S./C);%公式（5.8）求相位

figure,imshow(delta,[])%也可以试一下imshow(delta)

根据相位展开原理，按照下图的指示用几个条件语句即可实现扩展到0~2π范围，需要注意的是对S、C矩阵的每一个对应元素进行判断，不是对矩阵直接判断。可用下列命令获得矩阵的行数和列数：

x=size(delta,1);%行数

y=size(delta,2);%列数

0~2π相位展开方法

连续相位展开方法

连续相位的计算方法看起来比较简单，但是实际用代码实现还是有点绕，很容易逻辑混乱。好在matlab自带的函数unwrap()可以实现这一功能，只需要对前面得到的0~2π范围内的包裹相位使用unwrap函数就可以变换到连续相位。这里的注意点则是unwrap函数只能进行对矩阵的列或行进行相位矫正，因此需要运用两次才能实现对整个矩阵的相位矫正。

其实在应用unwrap函数时发现它是对数据加减2π，那么能在-π/2~π/2扩展到0~2π范围这一操作中使用吗？我试过了不能实现，但是如果读了unwrap函数的源代码，就可以找到技巧了，并能够自己写代码实现unwrap的功能。unwrap函数的源代码如下：

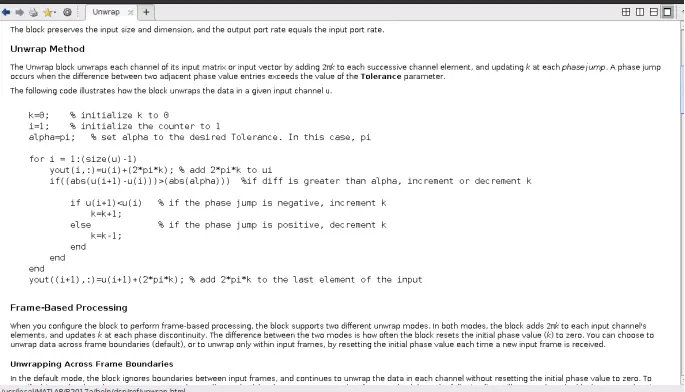
unwrap函数代码

以上就是本人对该问题的相关经验分享，在这之前我也不怎么用过matlab，花了几天时间才写出了代码。按照上面思路来做，能少走一些弯路，估计两三个小时就能解决，至于很多的代码细节问题还是需要自己去查找。如果想直接获取源代码，可以私聊（有收费，不保证一定正确，不包调试，一锤子买卖），拒绝白嫖。忠告：代码难度不大，尽量还是动用自己的小脑袋做一遍吧！！！

下面就是计算结果：