MATLAB中的平移、旋转与缩放技巧

空间描述和变换是机器人学的基础，这里举了两个matlab例子用来展现平面上的平移、旋转缩放的是如何实现的。具体的理论部分，可以参阅更多的机器人学相关书籍。

将一个正方形旋转、平移并缩放

% 定义正方形的初始坐标
x = [0 0 1 1];
y = [0 1 1 0];

% 将正方形绘制出来
figure(1);clf; hold on;
plot(x([1 2 3 4 1]), y([1 2 3 4 1]), 'b', 'LineWidth', 2);
axis([-1 2 -1 2]);  % 设置坐标轴范围

% 定义变换矩阵
T = [cosd(45) -sind(45) 10; sind(45) cosd(45) 10; 0 0 0.7];

% 将正方形进行变换
new_xy = T * [x; y; ones(size(x))];

% 绘制变换后的正方形
plot(new_xy(1,[1 2 3 4 1]) .* new_xy(3,[1 2 3 4 1]), ...
    new_xy(2,[1 2 3 4 1]) .* new_xy(3,[1 2 3 4 1]), 'r', 'LineWidth', 2);
axis([-1 20 -1 20]);  % 设置坐标轴范围
axis equal;
legend('原始正方形', '变换后的正方形');

这里面将正方形旋转了45度，并且平移了（10,10）的距离，最后绘制时要乘以缩因子0.7。由于最后来缩放，所以缩放的中心为原点，正方形变换到(7,7)的位置。

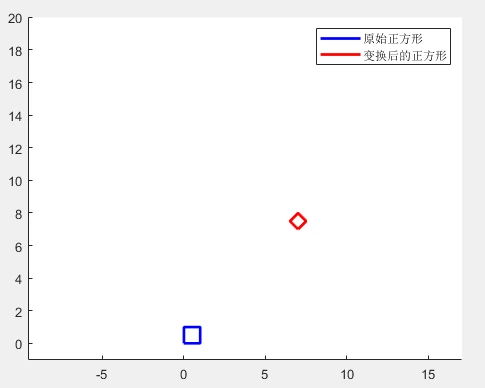
2.先选择缩放再平移

%%
% 定义正方形的初始坐标
x = [0 0 1 1];
y = [0 1 1 0];

% 将正方形绘制出来
figure(2);clf;hold on
plot(x([1 2 3 4 1]), y([1 2 3 4 1]), 'b', 'LineWidth', 2);
axis([-1 12 -1 12]);  % 设置坐标轴范围

% 定义变换矩阵
T1 = [cosd(60) -sind(60) 0; sind(60) cosd(60) 0; 0 0 1];  % 旋转
S = [0.5 0 0; 0 0.5 0; 0 0 1];  % 缩放 0.5
T2 = [1 0 10; 0 1 10; 0 0 1];  % 平移


% 将正方形进行变换
M = T2 * S * T1;  % 变换矩阵
new_xy = M * [x; y; ones(size(x))];

% 绘制变换后的正方形
hold on;
plot(new_xy(1,[1 2 3 4 1]), new_xy(2,[1 2 3 4 1]), 'r', 'LineWidth', 2);
axis([-1 12 -1 12]);  % 设置坐标轴范围
axis equal;
legend('原始正方形', '变换后的正方形','Location','best');

注意的是，S = [0.5 0 0; 0 0.5 0; 0 0 1]; 对角线上的元素都是0.5，，其他元素都是0。在二维坐标系中，对角线上的元素代表了x轴和y轴上的缩放因子，而其他元素代表了旋转或者错切等变换的因子。后面绘图时就没有再去乘以比例因子了。