内容介绍

摘要

光学干涉成像是一种无透镜成像技术，它利用光波的干涉特性来重建被测物体的图像。与传统的透镜成像技术相比，光学干涉成像具有许多优点，例如成像分辨率高、成像速度快、成像成本低等。然而，光学干涉成像也存在一些挑战，例如成像过程中的相位噪声和散斑噪声等。

为了解决这些挑战，近年来，非凸优化方法在光学干涉成像领域得到了广泛的应用。非凸优化方法能够有效地处理相位噪声和散斑噪声，从而提高光学干涉成像的图像质量。

非凸优化方法在光学干涉成像中的应用

非凸优化方法在光学干涉成像中的应用主要体现在以下几个方面：

• 相位噪声抑制：相位噪声是光学干涉成像中的一种主要噪声源，它会降低图像的质量。非凸优化方法能够有效地抑制相位噪声，从而提高图像质量。
• 散斑噪声抑制：散斑噪声是光学干涉成像中另一种主要噪声源，它会使图像产生斑点状的噪声。非凸优化方法能够有效地抑制散斑噪声，从而提高图像质量。
• 图像重建：图像重建是光学干涉成像中的一个关键步骤，它将干涉图重建为被测物体的图像。非凸优化方法能够有效地解决图像重建问题，从而提高图像质量。

部分代码

function [M_s, M_s_conj, M_s_zero, M_s_large, M1, M2, M3, M_p,count] = ...         create_mask_freq_selection_power_bi(Ti,n,m,M_b,u_lf,seed,c)% c : vector position of 0 freq% u_lf : low frequency proprotion in bispectrumcount = 0;Ti = Ti(1:end-1,:) ;[mask_ind,M_p] = generate_idx_mask(n,m, unique(Ti(:)) ) ;mask = zeros(n*m,1) ;mask(mask_ind) = 1 ;M_s_large = reshape(mask,n,m) ;% figure, imagesc(M_s_large)M_s = zeros(n,m) ;M_s(:, 1:m/2) = M_s_large(:, 1:m/2) ;M_s(1:n/2+1, m/2+1) = M_s_large(1:n/2+1, m/2+1) ;% % % figure, imagesc(M_s)M_s_conj = zeros(n,m) ;M_s_conj(:, m/2+2:end) = M_s_large(:, m/2+2:end) ;M_s_conj(n/2+1:end, m/2+1) = M_s_large(n/2+1:end, m/2+1) ;% % % figure, imagesc(M_s_conj)M_s_large(n/2+1, m/2+1) = 1 ;M_s_zero = zeros(n,m) ;M_s_zero(n/2+1, m/2+1) = 1 ;M_s = logical(M_s) ;M_s_conj = logical(M_s_conj) ;M_s_zero = logical(M_s_zero) ;% select bispectra -------------------------------------------------------T = zeros(M_b,3) ;i0 = 1 ;% select bispectra from low freq.M_hf = floor(u_lf*n*m) ;if M_hf < 2*M_p[ ~, Tib ] = mask_1D_select_freq( n,m,u_lf, 1/20, seed, c ) ;Tib = Tib(1:end-1,:) ;mask_ind_hf = generate_idx_mask(n,m, unique(Tib(:)) ) ;mask_ind_hf = intersect(mask_ind_hf, mask_ind) ;mask_hf = zeros(n*m,1) ;mask_hf(mask_ind_hf) = 1 ;M_hf = max(size(mask_ind_hf)) ;while 1Idx = randperm(M_hf) ;for j =1:length(Idx)-2idx = Idx(j:j+2) ;idx = sort(mask_ind_hf(idx))' ;if idx(1)~=c && idx(2)~=c && idx(3)~=cif sum(ismember(idx,T,'rows')) == 0 if ~(nnz(find(idx(1) == T)) && nnz(find(idx(2) == T)) && nnz(find(idx(3) == T)))    count = count + 1;endT(i0,:) = idx ;i0 = i0+1 ;endendif i0>floor(0.9*M_b)    breakendendif i0>floor(0.9*M_b)     breakendendend% select remaining bispectrafor i = i0:M_bidx = [c,c,c] ;while idx(1)==c || idx(2)==c || idx(3)==cwhile 1idx = sort(randperm(M_p*2,3)) ;idx = mask_ind(idx)' ;if sum(ismember(idx,T,'rows')) == 0     breakendendendif ~(nnz(find(idx(1) == T)) && nnz(find(idx(2) == T)) && nnz(find(idx(3) == T)))    count = count + 1;endT(i,:) = idx ;end% build vectors of indices for bispectrum ---------------------------------M1 = 0*T(:,1) ;M2 = 0*T(:,2) ;M3 = 0*T(:,3) ;for i =1:M_bM1(i) = sum(mask(1:T(i,1))) ;M2(i) = sum(mask(1:T(i,2))) ;M3(i) = sum(mask(1:T(i,3))) ;endendfunction [mask_ind,M_p] = generate_idx_mask(n,m, mask_ind_inf )% frequency space sampling: symmetrymask = zeros(n*m,1) ;mask(mask_ind_inf) = 1 ;mask = reshape(mask,n,m) ;Mask = zeros(n+1,m+1) ;Mask(1:end-1,1:end-1) = mask ;Mask = fliplr(flipud(Mask)) ;mask = Mask(1:end-1,1:end-1) ;% % % figure, imagesc(mask)mask = mask(:) ;mask_ind_sup = find(mask==1) ;% frequency space samplingmask_ind = [mask_ind_inf;mask_ind_sup] ;% number of powerspectraM_p = length(mask_ind_inf) ;end

运行结果

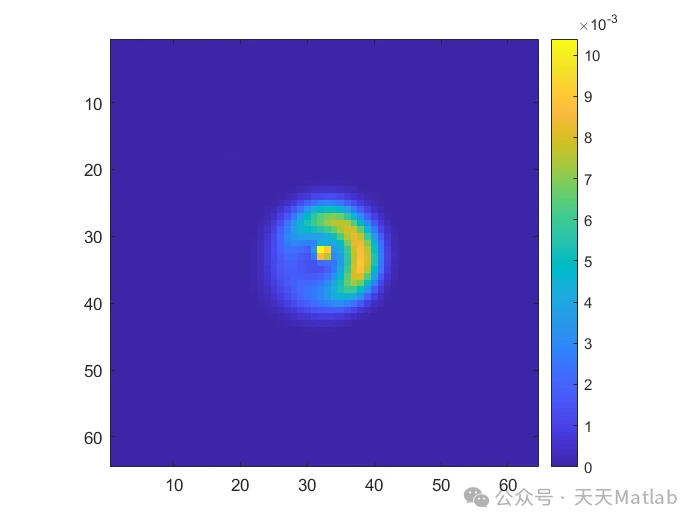
编辑

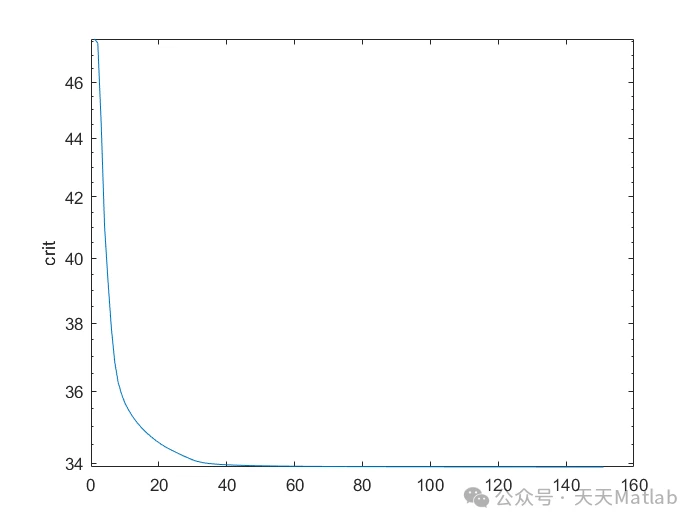
编辑

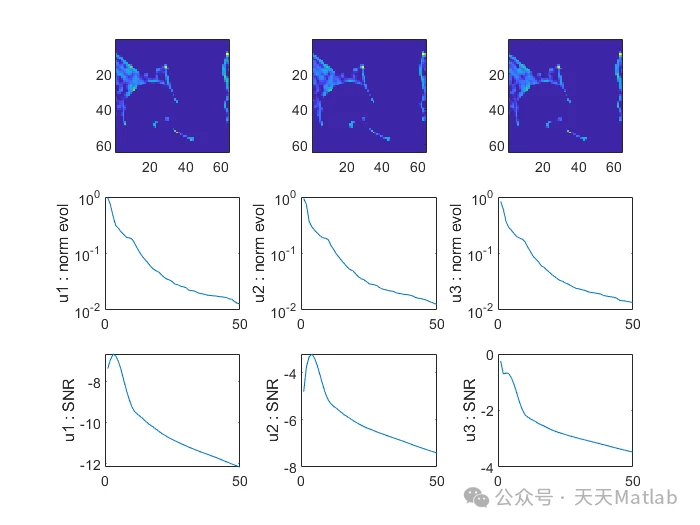
编辑

非凸优化方法在光学干涉成像中的挑战

非凸优化方法在光学干涉成像中的应用也面临着一些挑战，例如：

• 计算复杂度高：非凸优化方法的计算复杂度通常较高，这使得它们在实际应用中受到限制。
• 鲁棒性差：非凸优化方法的鲁棒性通常较差，这使得它们在处理噪声较大的数据时容易出现问题。
• 收敛速度慢：非凸优化方法的收敛速度通常较慢，这使得它们在实际应用中需要较长的时间。

总结

非凸优化方法在光学干涉成像领域得到了广泛的应用，并且取得了很好的效果。然而，非凸优化方法在实际应用中也面临着一些挑战。随着研究的深入，这些挑战有望得到解决，从而进一步提高光学干涉成像的图像质量。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删