ABAQUS心得：打开/关闭“几何非线性”时输出值的含义

• 关闭几何非线性的材料非线性问题，输出变量E的值实际为名义应变的值(此时E=NE)，但在查找真实应力S时当成真实应变处理，EE为弹性应变，PE的值为E-EE,此时对应的应力为输入的材料数据中数值等于E-EE对应的应力，而不是此时本应该的LE-EE对应的应力，造成应力偏大。且无法设置输出LE即真实应变和NE名义应变，其会被自动转成E。
• 打开几何非线性的材料非线性问题，输出场变量LE为真实应变，NE为名义应变，塑性应变PE为LE-EE，此时对应的应力即为输入的材料数据中数值等于LE-EE对应的应力值。

• 例如对于下列的应力数据

          C=A*(1+B)

          D=In(1+B)

          弹性模量=C/D

          F=D-C/弹性模量

将真实塑性应变用于定义材料后，对于使用该材料的变成为1mm的立方体块一端约束U2方向，另一端施加U2=0.4mm的位移荷载。在step模块分打开几何非线性和关闭几何非线性两种情况运行分析，结果如下：

对于打开几何非线性的模型：

（1）在U2=0.2mm时，此时的名义应变NE22云图如下，可见名义应变刚好为0.2/1=0.2：

（2）对数应变LE22云图如下，可见对数应变刚好为In(1+NE)=In(1+0.2)=0.1823

（3）真实应力S22云图如下，可见刚好为LE22=0.1823值所对应的应力值480MPa

（4）弹性应变EE22云图如下，可见刚好为S22/弹性模量,弹模为定义材料时输入的值，其应为200.19/0.0009495490356约等于210726MPa，所以为480/210726=2.277839e-3

（5）塑性应变PE22云图如下，可见刚好为PE22=LE22-EE22=0.1823-2.277839e-3=0.18002216,该塑性应变值对应的真实应力值刚好为480MPa，与输入的材料数据吻合。

对于关闭几何非线性的模型：

（1）在U2=0.2mm时，此时的总应变分量E22云图如下，可见其值为0.2，刚好与此时的名义应变值0.2/1=0.2相等,在石亦平的《ABAQUS有限元分析实例详解》第167页指出，此时的E为真实应变，按此说法云图显示的E22应等于In(1+0.2)=0.1823，与试验结果不符。但是在查看真实应力值时，S22为输入真实应力-真实应变曲线上真实应变为0.2时对应的应力值，可见ABAQUS在计算应力值时是把E22当作真实应变来对待的。但实际上此时的真实应变值不是0.2，应该为0.1823，总结：此时E22的值为名义应变的值，但是在查找真实应力时将其当作真实应变，可见ABAQUS确实认为E22的值为真实应变，只不过在计算E22值时采用计算名义应变NE22的公式，也就是在小变形的情况下把名义应变当作真实应变来处理。 

（2）真实应力S22云图如下，其值为真实应变等于0.2时所对应的应力值480MPa

继续查看E22=0.19>0.1823时对应的S22，可见还是为480MPa

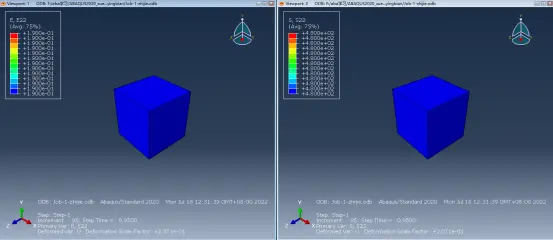
当E22=0.18<0.1823,其对应的S22为479.6MPa

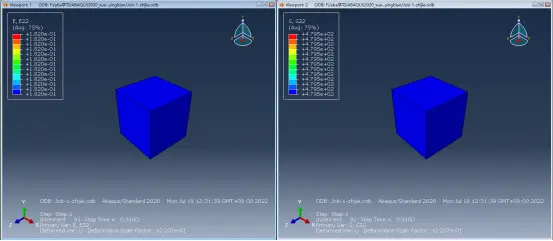
综上所述可以看出，ABAQUS在计算E22时是用此时的位移除以原始长度来计算的，也就是按名义应变计算公式来计算的，但是却又把按名义应变公式算出的E22的值当作真实应变来查找真实应力S22，所以会造成算出的应力值比实际值偏大，因为实际的真实应变LE总是小于此时的名义应变值NE的。例如，如下图所示，对于打开了几何非线性的模型，当U2=0.19mm时，名义应变NE=0.19/1=0.19，对应的真实应变LE22为In(1+0.19)=0.17395<0.1823，该值对应的真实应力值S22为476.7MPa：

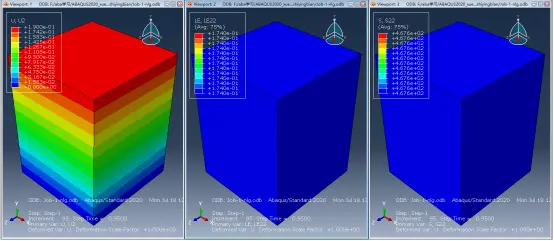
而对于关闭几何非线性的模型来说，当U2同样为0.19mm时，ABAQUS认为此时的真实应变E22等于名义应变NE22，即为0.19>0.1823，所以真实应变为0.19时对应真实应力480MPa，如下图所示：

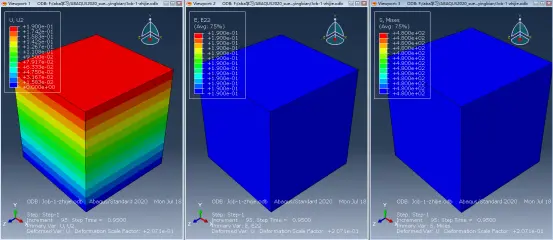
（3）弹性应变EE22云图如下，可见刚好为S22/弹性模量,弹模为定义材料时输入的值，其应为200.19/0.0009495490356约等于210726MPa，所以为480/210726=2.277839e-3，由于把名义应变当作真实应变去查找真实应力S22，所以弹性应变E22总是大于或者等于打开几何非线性模型的计算结果

（4）塑性应变PE22云图如下，可见刚好为PE22=E22-EE22=0.2-2.277839e-3=0.197722161。可见比打开几何非线性得到PE22=0.1800要大

 本人书面表达能力不是很强，万一有没看懂的地方或者不对的地方欢迎评论区指出，以免误人子弟。另外需要例子模型文件的可以私聊我获取