此块,我们将通过Tensorflow的游乐场来快速的介绍神经网络的主要功能。Tensorflow游乐场的链接如下所示:https://playground.tensorflow.org,这是一个可以通过网络浏览器就可以训练的简单的神经网络,并可以实现可视化训练过程的工具。其具体的截图如下所示:
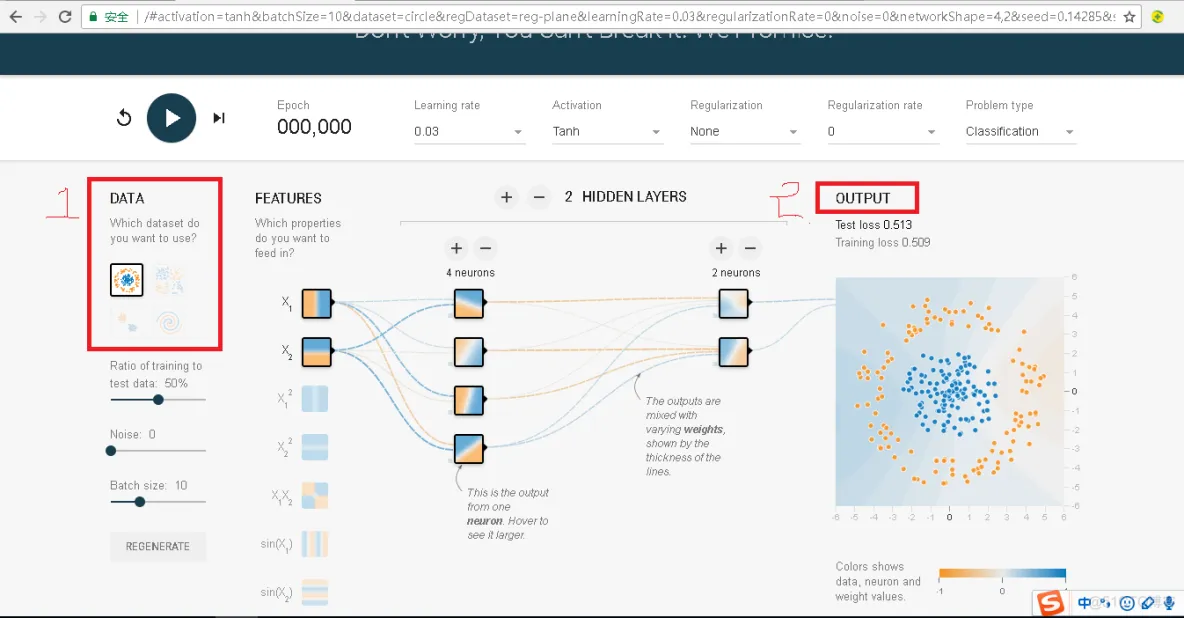
从上图可以看出,Tensorflow游乐场的左侧,标号为1的红色方框中提供了四种不同的【数据集合】用来测试神经网络。默认的数据集合被选择出来,并且看起来非常清晰。被选中的数据也会显示在右侧的输出端,例如途中标记为2的红色方框下,【OUTPUT】栏的下面,在这个数据集合中,我们可以看到一个二维的平面上有两种颜色的样本点,蓝色和橙色,每一个小点,代表一个【训练样本】,而【样本点】的颜色,代表了样本点的【类别标签】。因为样本点的颜色只有两种,所以,这是一个二分类问题。我们点击按钮运行后,这个样本很快的被划分为两类,如下图所示。

关于二分类的问题,再此块,我们可以举一个例子,假设我们需要判断某工厂生产的零件是否合格,那么蓝色的点可以表示工厂生产的零件不合格,橙色的表示零件和个,这样就将一个零件是否合格转化成了区分颜色的点。
为例将一个在实际环境中遇到的问题转化成二维平面上对应的点,就需要考虑如何将实际问题张的实体转化成二维平面上的一个样本点。这就是【特征提取】需要解决问题。
还是以零件为例,我们可以使用零件的长度和质量大致的描述一个零件,这样一个物理意义上的零件就可以被转化成长度和质量这两个数字。在机器学习中,所有用于描述实体的数组组合在一起,就是一个【实体】的【特征向量】。在Tensorflow中的Feature一栏,对应的就是一个零件的特征向量,在此块,我们可以认为x1代表两件的质量,x2代表零件的长度。
【特征向量】是【神经网络】的【输入】,神经网络的主体,在上图的中间部分。就目前而言,主流的神经网络都是分层的结构。第一层为【输入层】,代表【特征向量】中每一个特征的取值或者【属性】,而且每一层只和下一层连接,直到最后一层作为输出层得到计算的结果。在二分类问题中,比如判断零件是否合格,神经网络的输出层往往只包含一个节点,这个节点最终的输出输一个实数。通过这个输出值和一个事先设定的阈值,就可以得到分类的结果。
在【输入层】和【输出层】之间的层叫做【隐藏层】,一般一个神经网络的【隐藏层】越多,这个网络的深度就越深。而所谓的深度神经网络或者深度学习的这个深度也是和神经网络的层数密切相关的。在Tensorflow游乐场中点击+和-按钮,就可以用来增加和减少神经网络的【隐藏层】。
在Tensorflow的游乐场中,除了可以选择神经网络的深度,它也支持选择神经网络每一层节点的【节点】的数量,以及:
【1】学习率-------Learning Rate
【2】激活函数-----Activation Function
【3】 正则化------Regularization
在上图中,一个小方框代表神经网络中的一个【节点】,方框与方框之间的边代表节点之间的连接。,每一条【边】代表了神经网络中的【一个参数】,它可以是【任意的实数】。【神经网络】就是通过对【参数】的【合理设置】来解决【分类】或者【回归问题】,边上的颜色,代表了这个参数的取值,颜色越深,这个参数的绝对值越大。
综上所述,使用【神经网络】解决【分类问题】主要可以分为以下4个步骤:
【1】提取【问题】中【实体】的【特征向量】作为神经网络的【输入】。
【2】定义【神经网络的结构】,并定义如何从神经网络的输入得到输出,该过程就是【神经网络的前向传播算法】。
【3】通过【训练数据】来调整【神经网络】中【参数】的取值,这就是【训练神经网络】的【过程】
【4】使用【训练好的神经网络】来预测未知的【数据】。
此块,对于神经网络中的前向的传播算法仅仅只是进行一个简单的简介,更为详细的神经网络的前向传播算法的推导及其数学分析,请关注随后的学习笔记。
在前面的介绍了【神经网络】可以将输入的【特征向量】经过层层的推导得到最后的【输出】,并且通过这些输出,解决【 分类】或者【回归】的问题。那么,神经网络的输入是如何得到的呢?这就是我们这块要说的【前向传播算法】。
不同的【神经网络结构】的【前向传播方式】是不一样的。此块,我们介绍一下最简单的【全连接神经网络】的【前向传播 算法】,并且将展示如何通过Tensorflow实现这个算法。
为了介绍【神经网络】的【前向传播算法】,我们需要首先了解一下【神经元】的结构,【神经元】是【神经网络】中最小的单元,对应神经网络中的【节点】。
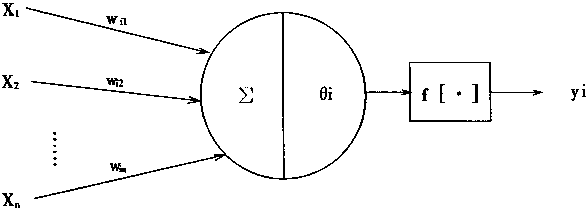
如上图所示,一个【神经元】有多个输入和一个输出,每个神经元的输入既可以是其他神经元的输出也可以是整个神经网络的输入。所谓的不同的【神经网络结构】其实质就是不同【神经元】之间的【连接结构】。一个最简单的【神经元结构】就是所有输入的【加权和】,而不同输入的【权重】就是神经网络的【参数】。【神经网络】的【优化过程】就是【优化神经元参数取值】的过程。
计算【神经网络】的【前向传播】结果需要【三部分信息】。第一部分就是【神经网络】的【输入】,这个输入就是从实体中提取的【特征向量】。第二部分就是【神经网络】得【连接结构】。
经过一些列推导之后,我们可以将【神经网络】的【前向传播算法】使用【矩阵乘法】的方式表达出来,而在Tensorflow中,矩阵乘法是非常容易实现的。
import tensorflow as tf
a = tf.matmul(X,W1)
y = tf.matmul(A,W2)
#========================================================================================================
#【1】其中,X是一个行向量,具体的数值为X = [x1,x2],对应于神经网络输入层的两个节点
#【2】W对应全连接方式的第一层神经元节点的【权值】,是一个2行3列的矩阵,具体的数值为W=[[w11,w12,w13],[w21,w22,w23]]
#【3】则第一层的前向传播为XW,用tensorflow中的代码表示就如上所示。
#========================================================================================================
其中tf.matmul()实现了【矩阵乘法】的【功能】。到此为止,已经简述了神经网络的前向传播算法,并且给出了Tensorflow的程序实现了这个过程。之后,我们将继续介绍:
【1】偏置-------------bias
【2】激活函数--------activation function
等更加复杂的神经元结构。也将会介绍卷积神经网络Tensorflow的实现过程、LSTM结构等更加复杂的神经网络结构。对于这些更加复杂的神经网络,Tensorflow也提供了的支持。
【神经网络】中的【参数】是【神经网络】实现【分类】或者【回归】问题中的重要部分。此块,我们将更加具体的介绍Tensorflow是如何【组织】、【保存】以及【使用】神经网络中的【参数】的。
在Tensorflow中,变量tf.Variable()函数的作用就是【保存】和【更新】神经网络中的【参数】。和其他的编程语言相似,Tensorflow中的变量而需要进行初始化。而在神经网络中,给参数赋予随机的初始值是最为常见的,所以一般也使用Tensorflow的随机数给Tensorflow中的变量初始化。下面的代码给出了一种在Tensorflow中声明一个2x3的矩阵变量的方法:
weights =tf.Variable(tf.random_normal([2,3],mean=0,stddev=2))
这段代码调用了Tensorflow中的【变量声明函数】tf.Variable。在【变量声明函数】中,给出了初始化这个变量的方法。Tensorflow中的变量的初始值可以设置成【随机数】、【常数】或者调用其他变量的初始化计算得到。在上面的代码中,使用正太分布的随机函数random_normal产生了一个2行3列分矩阵。
在【神经网络】中,【偏置项:bias】通常会使用【常数】来设置【初始值】。下面的代码给出了一个样例。
bias = tf.Variable(tf.zeros[3])
在Tensorflow中,一个变量的值,在被使用之前,这个变量的初始化必须被明确的调用。下面的样例介绍了如何通过【变量】实现神经网络的【参数】并实现【神经网络】【前向传播的过程】。
#========================================================================================================
#函数原型:
# def random_normal(shape,mean=0.0,stddev=1.0,dtype=dtypes.float32,seed=None,name=None)
#函数说明:
# 生成一个满足【正太分布】的随机数集合,集合的维度为shapee,均值为mean,标准方差为stddev,
#========================================================================================================
import tensorflow as tf
#【1】声明w1、w2这两个【变量】,这里还通过seed参数设置了随机种子,这样可以保证每次运行得到的结果是一样的。
w1 = tf.Variable(tf.random_normal([2,3],mean=0,stddev=1,seed=1))
w2 = tf.Variable(tf.random_normal([2,3],mean=0,stddev=1,seed=1))
#【2】暂时将【输入的特征向量】定义为一个【常量】,注意这里的x是一个1行2列的矩阵
x = tf.constant([0.7,0.9])
#【3】通过矩阵乘法计算【神经网络】的【前向传播】
a = tf.matmul(x,w1)
y = tf.matmul(a,w2)
#【4】网络定义好之后,即Tensorflow中的【图】定义好之后,使用【会话】Session开始运行
sess = tf.Session() #【1】创建一个【会话】Session
#【5】注意,这里不能通过sess.run(y)来获取y的值,因为w1和w2都还没有运行初始化的过程。
sess.run(w1.initializer) #【2】初始化w1
sess.run(w2.initializer) #【3】初始化w2
#【6】输出
print(sess.run(y))
sess.close()
上面的这段程序,实现了【神经网络】的【前向传播过程】。从这段的代码可以看到,当声明了变量w1、为之后,可以通过w1和w2来定义神经网络中的前向传播过程并得到中间的结果a和最后的答案y。定义w1、w2、a和y的部分对应的是第一步,则一步定义了Tensorflow【图】中所有的计算,但是,这些被定义的计算在这不并没有真正的运行。当需要运行这些计算并得到具体的数字的时候,需要进入到Tensorflow程序中的第二步。
在Tensorflow程序中的第二步,会声明一个【会话:Session】,并通过会话计算结果。在上面的代码中,当【会话Session】的定义之后,就可以运行定义好的计算了。但是,需要特别注意的一点是,在具体的运行之前,需要明确的初始化所有即将用到的【变量】。
虽然,直接调用每个【变量】的【初始化】过程,是一个可行的方案,但是当【变量】的数目变多,或者【 变量】之间存在着依赖关系的时候,单个调用的方案就显的比较麻烦。为例解决这个问题,Tensorflow提供了一种更加便捷的方式来完成【变量】的【初始化】过程。下面的程序展示了通过tf.initializer_all_variables函数实现所有【变量】初始化的过程。
init_op = tf.initialize_all_variables()
sess.run(init_op)
通过tf.initialize_all_variables()函数,就不需要将变量一个一个的初始化,这个函数也会自动处理变量之间的依赖关系。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删